平面向量的数量积[下学期]
图片预览











文档简介
课件31张PPT。平面向量的数量积 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习 复 习例题讲解小结回顾引 入
新课讲解性质讲解课堂练习我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θS力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习θ=180°θ =90°
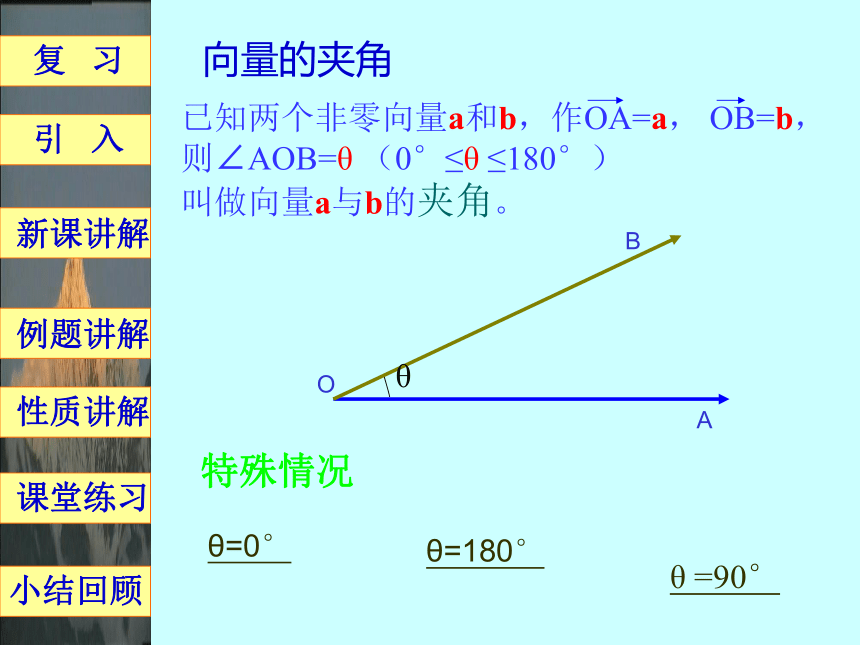
向量的夹角已知两个非零向量a和b,作OA=a, OB=b,则∠AOB=θ (0°≤θ ≤180°)
叫做向量a与b的夹角。
θ=0°特殊情况OBAθ 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习已知两个非零向量a与b,它们的夹角为θ,我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),记作a·b
a·b=|a| |b| cosθ
规定:零向量与任一向量的数量积为0。 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习解:a·b=|a||b|cosθ
=5×4×cos120°
=5×4×(-1/2)= -10.例1.已知|a|=5,|b|=4,a与b的夹角
θ=120°,求a·b. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习我们得到a·b的几何意义:
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习例1.已知|a|=5,|b|=4,a与b的夹角
θ=120°, 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则
(1)e·a=a·e = |a| cosθ重要性质:(5)|a·b|≤|a||b| 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习课堂练习判断下列各题是否正确(1)若a=0,则对任意向量b,有a·b=0-----
(2)若a≠0,则对任意非零向量b,有a·b≠0--
(3)若a≠0,且a·b=0,则b=0 -------------------
(4)若a·b=0,则a=0或b=0 ---------------------
(5)对任意向量a有a2=│a│2 ----------------
(6)若a≠0且a·b=a·c,则b=c -------------------
(√)(× )( ×)(× )(√ )(× ) 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习基础练习 1、判断下列命题的真假:2、已知△ABC中,a =5,b =8,C=600,求 3、已知 | a | =8,e是单位向量,当它们之间的夹角为
则 a在e方向上的投影为 (1)平面向量的数量积可以比较大小
(2)
(3)已知b为非零向量因为0×a =0, a ·b = 0,所以a = 0
(4 ) 对于任意向量a、 b、 c,都有a ·b ·c = a·(b ·c)进行向量数量积
计算时,既要考
虑向量的模,又
要根据两个向量
方向确定其夹角。例1、 已知(a – b)⊥(a + 3 b),
求证: | a + b |= 2 | b |.例2、已知a、b都是非零向量,且a + 3 b 与 7 a – 5 b 垂直,a – 4 b 与7 a – 2 b垂直, 求a与b的夹角. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习作业布置: 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习谢谢大家当θ=0°时,a与b同向返回当θ=180°时,a与b反向。
返回θ =90°,a与b垂直,记作a⊥b。返回返回当θ=0°时,它是|b|返回当θ=180°时,它是-|b|。
返回当θ=90°,它是0。
当θ为锐角时,它是正值;
返回当θ为钝角时,它是负值;
返回
新课讲解性质讲解课堂练习 复 习例题讲解小结回顾引 入
新课讲解性质讲解课堂练习我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θS力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习θ=180°θ =90°
向量的夹角已知两个非零向量a和b,作OA=a, OB=b,则∠AOB=θ (0°≤θ ≤180°)
叫做向量a与b的夹角。
θ=0°特殊情况OBAθ 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习已知两个非零向量a与b,它们的夹角为θ,我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),记作a·b
a·b=|a| |b| cosθ
规定:零向量与任一向量的数量积为0。 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习解:a·b=|a||b|cosθ
=5×4×cos120°
=5×4×(-1/2)= -10.例1.已知|a|=5,|b|=4,a与b的夹角
θ=120°,求a·b. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习我们得到a·b的几何意义:
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习例1.已知|a|=5,|b|=4,a与b的夹角
θ=120°, 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则
(1)e·a=a·e = |a| cosθ重要性质:(5)|a·b|≤|a||b| 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习课堂练习判断下列各题是否正确(1)若a=0,则对任意向量b,有a·b=0-----
(2)若a≠0,则对任意非零向量b,有a·b≠0--
(3)若a≠0,且a·b=0,则b=0 -------------------
(4)若a·b=0,则a=0或b=0 ---------------------
(5)对任意向量a有a2=│a│2 ----------------
(6)若a≠0且a·b=a·c,则b=c -------------------
(√)(× )( ×)(× )(√ )(× ) 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习基础练习 1、判断下列命题的真假:2、已知△ABC中,a =5,b =8,C=600,求 3、已知 | a | =8,e是单位向量,当它们之间的夹角为
则 a在e方向上的投影为 (1)平面向量的数量积可以比较大小
(2)
(3)已知b为非零向量因为0×a =0, a ·b = 0,所以a = 0
(4 ) 对于任意向量a、 b、 c,都有a ·b ·c = a·(b ·c)进行向量数量积
计算时,既要考
虑向量的模,又
要根据两个向量
方向确定其夹角。例1、 已知(a – b)⊥(a + 3 b),
求证: | a + b |= 2 | b |.例2、已知a、b都是非零向量,且a + 3 b 与 7 a – 5 b 垂直,a – 4 b 与7 a – 2 b垂直, 求a与b的夹角. 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习作业布置: 复 习例题讲解小结回顾 引 入
新课讲解性质讲解课堂练习谢谢大家当θ=0°时,a与b同向返回当θ=180°时,a与b反向。
返回θ =90°,a与b垂直,记作a⊥b。返回返回当θ=0°时,它是|b|返回当θ=180°时,它是-|b|。
返回当θ=90°,它是0。
当θ为锐角时,它是正值;
返回当θ为钝角时,它是负值;
返回
