2.4 平面向量的数量积及运算律(1)[下学期]
文档属性
| 名称 | 2.4 平面向量的数量积及运算律(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-22 10:28:00 | ||
图片预览





文档简介
课件16张PPT。回顾思考:前面我们学习了向量的哪几种运算?实际应用背景: 力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
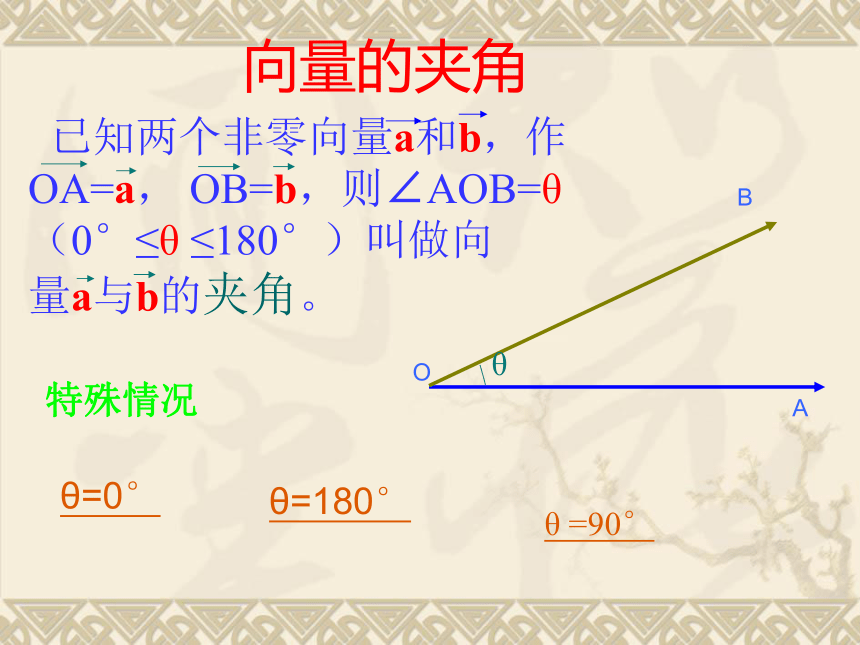
θ=180°θ =90°
向量的夹角θ=0°特殊情况 已知两个非零向量a与b它们的夹角为θ,我们把数|a|b|cosθ叫做a与b的数量积(或积),记作a·b即a·b=|a| |b| cosθ
规定:零向量与任一向量的数量积为0。
数量积定义注意: (1)两向量的数量积是一个数量,而不是向量,
符号由夹角决定;(2)a · b不能写成a×b ; 1) 对实数a≠0,若a · b=0,则b=0,但对向量a≠0 时,若a · b=0 , 能不能推出b是零向量? 2)对于实数a、b、c(b≠0),若a · b=b · c,则
a=c , 对于向量a,b,c , 此式是否仍成立呢? (3)向量的数量积与实数积的区别: a·b=|a| |b| cosθ(不能)3)对于实数a、b、c,有(a · b) · c=a · (b · c)
但对于向量a,b,c来说,此式是否一定成立? 5)已知向量 和实数 ,可以验证向量的数量积满足:(数乘结合律)若证明:若证明:设 夹角为 , 所以(交换律)4)已知向量 ,可以验证向量的数量积满足:6)已知向量 ,还可以验证向量的数积足:(分配律)平面向量数量积的运算律已知向量 和实数 ,则向量的数量积满足:注意:数量积运算不满足结合律设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则
(1)e·a=a·e = |a| cosθ数量积重要性质:(3)当a与b同向时,a·b=|a||b|;
(5)|a·b|≤|a||b| 当a与b反向时,a·b=-|a||b|;a·b=|a| |b| cosθ1.若a=0,则对任一向量b ,有a · b=0
2.若a≠0,则对任一非零向量b,有a · b≠0
3.若a≠0,a · b=0,则b=0
4.若a · b=0,则a · b中至少有一个为0
5.若a≠0,a · b= b · c,则a=c
6.若a · b= a · c ,则b≠c,当且仅当a=0时成立
7.对任意向量a , b ,c,有(a · b)·c≠a ·(b · c)
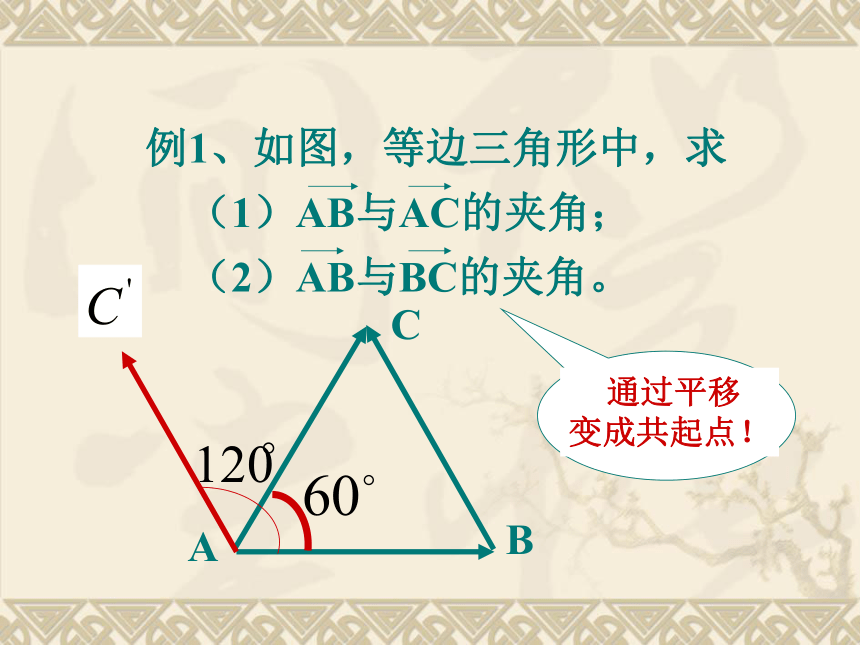
8.对任一向量a,有a2=|a|2 练习:判断正误( √ )( × )( × )( × )( × )( × )( × )( √ )练习:钝角C1 . a·b=|a| |b| cosθ
2. 数量积几何意义3. 重要性质小结:当θ=0°时,a与b同向返回当θ=180°时,a与b反向。
返回θ =90°,a与b垂直,记作a⊥b。返回
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
θ=180°θ =90°
向量的夹角θ=0°特殊情况 已知两个非零向量a与b它们的夹角为θ,我们把数|a|b|cosθ叫做a与b的数量积(或积),记作a·b即a·b=|a| |b| cosθ
规定:零向量与任一向量的数量积为0。
数量积定义注意: (1)两向量的数量积是一个数量,而不是向量,
符号由夹角决定;(2)a · b不能写成a×b ; 1) 对实数a≠0,若a · b=0,则b=0,但对向量a≠0 时,若a · b=0 , 能不能推出b是零向量? 2)对于实数a、b、c(b≠0),若a · b=b · c,则
a=c , 对于向量a,b,c , 此式是否仍成立呢? (3)向量的数量积与实数积的区别: a·b=|a| |b| cosθ(不能)3)对于实数a、b、c,有(a · b) · c=a · (b · c)
但对于向量a,b,c来说,此式是否一定成立? 5)已知向量 和实数 ,可以验证向量的数量积满足:(数乘结合律)若证明:若证明:设 夹角为 , 所以(交换律)4)已知向量 ,可以验证向量的数量积满足:6)已知向量 ,还可以验证向量的数积足:(分配律)平面向量数量积的运算律已知向量 和实数 ,则向量的数量积满足:注意:数量积运算不满足结合律设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则
(1)e·a=a·e = |a| cosθ数量积重要性质:(3)当a与b同向时,a·b=|a||b|;
(5)|a·b|≤|a||b| 当a与b反向时,a·b=-|a||b|;a·b=|a| |b| cosθ1.若a=0,则对任一向量b ,有a · b=0
2.若a≠0,则对任一非零向量b,有a · b≠0
3.若a≠0,a · b=0,则b=0
4.若a · b=0,则a · b中至少有一个为0
5.若a≠0,a · b= b · c,则a=c
6.若a · b= a · c ,则b≠c,当且仅当a=0时成立
7.对任意向量a , b ,c,有(a · b)·c≠a ·(b · c)
8.对任一向量a,有a2=|a|2 练习:判断正误( √ )( × )( × )( × )( × )( × )( × )( √ )练习:钝角C1 . a·b=|a| |b| cosθ
2. 数量积几何意义3. 重要性质小结:当θ=0°时,a与b同向返回当θ=180°时,a与b反向。
返回θ =90°,a与b垂直,记作a⊥b。返回
