华师大版八年级上册11.2.1 实数 (第一课时) 课件 (共22张PPT)
文档属性
| 名称 | 华师大版八年级上册11.2.1 实数 (第一课时) 课件 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 08:21:42 | ||
图片预览








文档简介
(共22张PPT)
11.2 实数(1)
-2 -1 0
学习目标
1.了解无理数和实数的意义;
2.能对实数进行分类.
3.理解实数与数轴上的点的关系.
1.有理数包括哪些数?
2.有理数中的分数能化为小数吗?
化为什么样的小数?举例加以说明.
回顾思考
定 义
无理数:
无限不循环小数叫做无理数
(irrational number).
实数:
有理数与无理数统称为实数
(Real numbers).
自主探究
要求学生自主阅读课本内容及阅读材料.
无限不循环小数叫做无理数
( 强调: 无限、不循环.)
(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)
无理数常见的几种典型:
一定要知道:
(2)无理数不一定都是用根号表示的数.如:π
(3)无理数有无数多个.
(4)无理数可分为正无理数和负无理数.
(1)用根号表示的数不一定是无理数.如:
判定一个数是否无理数:
(1)是看它是不是无限小数;(2)看它是不是不循环小数;(3)所有的有理数都能写成分数形式,但无理数则不能;
具体从以下几方面来判断:
(1)开方开不尽的数是无理数;
(2) 是无理数;
(3)无理数与有理数的和、差一定是无理数;
(4)无理数与有理数(不为0)的积、商一定是无理数;
判断的方法:
≈
≈
≈
≈
≈
≈
≈
1.414
1.732
2.646
2.449
2.236
2.828
3.162
常 用(要求熟记)
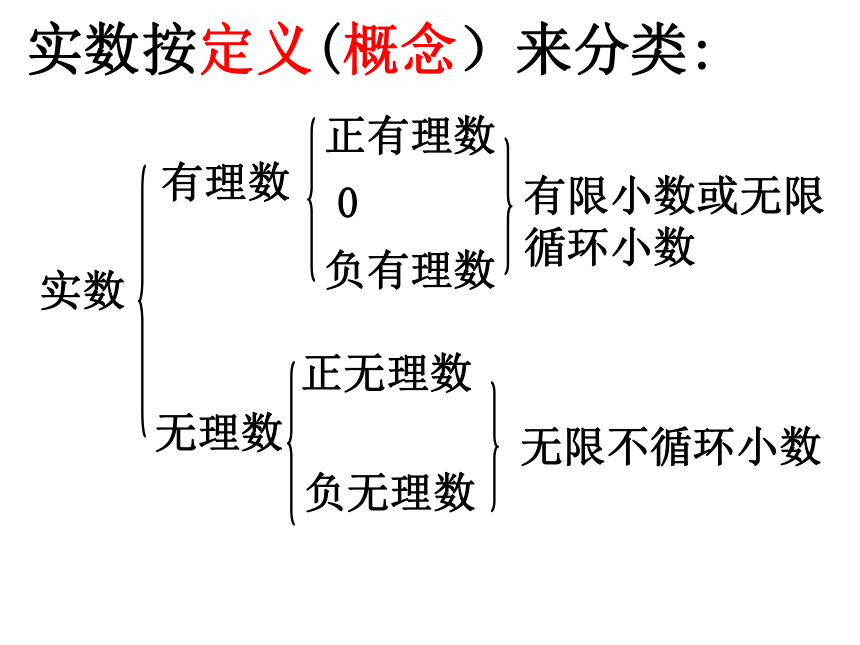
实数按定义(概念)来分类:
实数
正有理数
有理数
无理数
负有理数
0
负无理数
正无理数
有限小数或无限循环小数
无限不循环小数
负实数
正实数
数实
正有理数
负有理数
按正负性(性质符号)分类:
0
正无理数
负无理数
0
正实数
负实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.有理数的运算法则及运算律对实数仍然适用.
例如:
与 互为相反数
与 互为倒数
例1.
在
中
整数有:
有理数有:
无理数有:
1.判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并说明理由.
(1)无理数都是开方开不尽的数.( )
(2)无理数都是无限小数.( )
(3)无限小数都是无理数.( )
(4)无理数包括正无理数、零、负无理数( )
(5)不带根号的数都是有理数.( )
(6)带根号的数都是无理数.( )
(7)有理数都是有限小数.( )
(8)实数包括有限小数和无限小数.( )
练一练
有理数集合
无理数集合
2.把下列各数分别填入相应的集合内.
你能在数轴上找到表示 的点吗?
思考:
=?
探究:
1
1
动手操作:将两个边长为1的正方形剪拼成一个大正方形.
0
1
-1
在数轴上找表示 的点
思考:在数轴上你能找出表示 的点吗?
归纳
如果将所有的有理数都标到数轴上,那么数轴将被填满吗
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应
3、绝对值等于 的数是 , 的平方 是 .
一、填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
二、判断以下题目.
1.实数不是有理数就是无理数.
2.无理数都是无限不循环小数.
3.无理数都是无限小数.
4.带根号的数都是无理数.
5.无理数一定都带根号.
6.两个无理数之积不一定是无理数.
7.数轴上的任何一点都可以表示实数.
×
×
课堂小结:
1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可.
2.带根号的数并不都是无理数,而开方开不尽的数才是无理数.
3.掌握实数的不同分类法.
4. 实数与数轴上的点一一对应.
课外扩展
1.
2.化简:
3.实数a、b互为相反数,c、d互为负倒数,x的绝对值为 ,则代数式
11.2 实数(1)
-2 -1 0
学习目标
1.了解无理数和实数的意义;
2.能对实数进行分类.
3.理解实数与数轴上的点的关系.
1.有理数包括哪些数?
2.有理数中的分数能化为小数吗?
化为什么样的小数?举例加以说明.
回顾思考
定 义
无理数:
无限不循环小数叫做无理数
(irrational number).
实数:
有理数与无理数统称为实数
(Real numbers).
自主探究
要求学生自主阅读课本内容及阅读材料.
无限不循环小数叫做无理数
( 强调: 无限、不循环.)
(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)
无理数常见的几种典型:
一定要知道:
(2)无理数不一定都是用根号表示的数.如:π
(3)无理数有无数多个.
(4)无理数可分为正无理数和负无理数.
(1)用根号表示的数不一定是无理数.如:
判定一个数是否无理数:
(1)是看它是不是无限小数;(2)看它是不是不循环小数;(3)所有的有理数都能写成分数形式,但无理数则不能;
具体从以下几方面来判断:
(1)开方开不尽的数是无理数;
(2) 是无理数;
(3)无理数与有理数的和、差一定是无理数;
(4)无理数与有理数(不为0)的积、商一定是无理数;
判断的方法:
≈
≈
≈
≈
≈
≈
≈
1.414
1.732
2.646
2.449
2.236
2.828
3.162
常 用(要求熟记)
实数按定义(概念)来分类:
实数
正有理数
有理数
无理数
负有理数
0
负无理数
正无理数
有限小数或无限循环小数
无限不循环小数
负实数
正实数
数实
正有理数
负有理数
按正负性(性质符号)分类:
0
正无理数
负无理数
0
正实数
负实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.有理数的运算法则及运算律对实数仍然适用.
例如:
与 互为相反数
与 互为倒数
例1.
在
中
整数有:
有理数有:
无理数有:
1.判断正误,在后面的括号里对的用 “√”,错的记“×”表示,并说明理由.
(1)无理数都是开方开不尽的数.( )
(2)无理数都是无限小数.( )
(3)无限小数都是无理数.( )
(4)无理数包括正无理数、零、负无理数( )
(5)不带根号的数都是有理数.( )
(6)带根号的数都是无理数.( )
(7)有理数都是有限小数.( )
(8)实数包括有限小数和无限小数.( )
练一练
有理数集合
无理数集合
2.把下列各数分别填入相应的集合内.
你能在数轴上找到表示 的点吗?
思考:
=?
探究:
1
1
动手操作:将两个边长为1的正方形剪拼成一个大正方形.
0
1
-1
在数轴上找表示 的点
思考:在数轴上你能找出表示 的点吗?
归纳
如果将所有的有理数都标到数轴上,那么数轴将被填满吗
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应
3、绝对值等于 的数是 , 的平方 是 .
一、填空
2、 的相反数是 ,绝对值是 .
4、比较大小:-7
1、正实数的绝对值是 ,0的绝对值是 ,
负实数的绝对值是 .
它本身
0
它的相反数
5、一个数的绝对值是 ,则这个数是 .
二、判断以下题目.
1.实数不是有理数就是无理数.
2.无理数都是无限不循环小数.
3.无理数都是无限小数.
4.带根号的数都是无理数.
5.无理数一定都带根号.
6.两个无理数之积不一定是无理数.
7.数轴上的任何一点都可以表示实数.
×
×
课堂小结:
1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可.
2.带根号的数并不都是无理数,而开方开不尽的数才是无理数.
3.掌握实数的不同分类法.
4. 实数与数轴上的点一一对应.
课外扩展
1.
2.化简:
3.实数a、b互为相反数,c、d互为负倒数,x的绝对值为 ,则代数式
