华师大版八年级上册11.1.2 立方根课件(共17张PPT)
文档属性
| 名称 | 华师大版八年级上册11.1.2 立方根课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
课前准备:比较大小
11.1.2 立方根
学习目标
1、知道一个数的立方根的意义.
2、会用根号表示一个数的立方根.
3、会求一个数的立方根.
回顾与思考
1.计算下列各式.
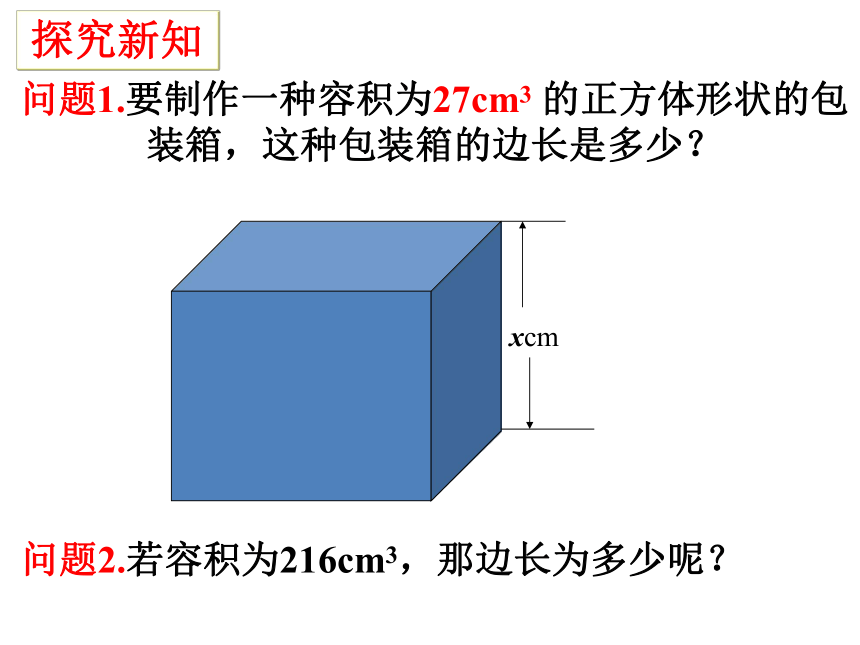
xcm
问题1.要制作一种容积为27cm3 的正方体形状的包装箱,这种包装箱的边长是多少?
问题2.若容积为216cm3,那边长为多少呢?
探究新知
上面所提出的问题,实质上就是要找一个数x,这个数x的立方等于216.即x3=216.
概 括
所以正方体的棱长应为6 cm.
因为63=216,
如果一个数的立方等于a,那么这个数就叫做a的立方根.
像平方根那样,6是216的立方根.
即:
(1) 27的立方根是什么?
(2) -27的立方根是什么?
(3) 0的立方根是什么?
任何数(正数、负数、零)的立方根如果存在的话,必定只有一个.
试一试
概 括
想一想
正数、负数、零的立方根的情况怎样?
3
-3
0
求一个数的立方根的运算,叫做开立方.
数a的立方根的表示方法
数a的立方根,
读作“三次根号a”.
a称为被开方数,3称为根指数,不可省略.
记作
例1
求下列各数的立方根.
⑴ 27 ⑵ -64 ⑶
⑷ 0 ⑸ 3 ⑹ -0.008
125
8
立方根的情况
⑴正数的立方根是正数;
⑵ 0的立方根是0本身;
⑶负数的立方根是负数.
任何数都
有立方根
例2
求下列各式的值.
⑴√27 - √8
3
2
⑵ √-8 +√9
3
(3)
7
8
-1
3
1.判断下列说法是否正确,并说明理由.
(2) 25的平方根是5
(3) -64没有立方根
(4) -4的平方根是±2
(5) 0的平方根和立方根都是0
(1)
的立方根是
当堂练习
2.求下列各式的值.
(1) ; ; .
(2)
(3)
能力提升:
平方根 立方根
正数
0
负数
两个平方根,它们
互为相反数
一个正的立方根
0
0
没有
一个负的立方根
立方根的特征
课堂小结
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
任何一个数 a 都只有一个立方根
课后思考:
填一填
(1)8的立方根与-8的立方根有什么关系?
(3)a的立方根与-a的立方根有什么关系?
(3)
它们互为相反数
2
(2)27的立方根与-27的立方根有什么关系?
它们互为相反数
它们互为相反数
总结:互为相反数的两个数的立方根也互为相反数.
扩展探究
已知4x2=144, y3+8=0, 求 x+y 的值.
由 4x2=144 ,
解:
得 x2=36
由 y3+8=0 ,
得 y3= -8
∴ x =±
√36
= ±6
∴ y =
√-8
3
= -2
①当 x =6, y = -2时,
x + y = 6+(-2)=4
②当 x = -6, y = -2时,
x + y = -6+(-2)= -8
课前准备:比较大小
11.1.2 立方根
学习目标
1、知道一个数的立方根的意义.
2、会用根号表示一个数的立方根.
3、会求一个数的立方根.
回顾与思考
1.计算下列各式.
xcm
问题1.要制作一种容积为27cm3 的正方体形状的包装箱,这种包装箱的边长是多少?
问题2.若容积为216cm3,那边长为多少呢?
探究新知
上面所提出的问题,实质上就是要找一个数x,这个数x的立方等于216.即x3=216.
概 括
所以正方体的棱长应为6 cm.
因为63=216,
如果一个数的立方等于a,那么这个数就叫做a的立方根.
像平方根那样,6是216的立方根.
即:
(1) 27的立方根是什么?
(2) -27的立方根是什么?
(3) 0的立方根是什么?
任何数(正数、负数、零)的立方根如果存在的话,必定只有一个.
试一试
概 括
想一想
正数、负数、零的立方根的情况怎样?
3
-3
0
求一个数的立方根的运算,叫做开立方.
数a的立方根的表示方法
数a的立方根,
读作“三次根号a”.
a称为被开方数,3称为根指数,不可省略.
记作
例1
求下列各数的立方根.
⑴ 27 ⑵ -64 ⑶
⑷ 0 ⑸ 3 ⑹ -0.008
125
8
立方根的情况
⑴正数的立方根是正数;
⑵ 0的立方根是0本身;
⑶负数的立方根是负数.
任何数都
有立方根
例2
求下列各式的值.
⑴√27 - √8
3
2
⑵ √-8 +√9
3
(3)
7
8
-1
3
1.判断下列说法是否正确,并说明理由.
(2) 25的平方根是5
(3) -64没有立方根
(4) -4的平方根是±2
(5) 0的平方根和立方根都是0
(1)
的立方根是
当堂练习
2.求下列各式的值.
(1) ; ; .
(2)
(3)
能力提升:
平方根 立方根
正数
0
负数
两个平方根,它们
互为相反数
一个正的立方根
0
0
没有
一个负的立方根
立方根的特征
课堂小结
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
任何一个数 a 都只有一个立方根
课后思考:
填一填
(1)8的立方根与-8的立方根有什么关系?
(3)a的立方根与-a的立方根有什么关系?
(3)
它们互为相反数
2
(2)27的立方根与-27的立方根有什么关系?
它们互为相反数
它们互为相反数
总结:互为相反数的两个数的立方根也互为相反数.
扩展探究
已知4x2=144, y3+8=0, 求 x+y 的值.
由 4x2=144 ,
解:
得 x2=36
由 y3+8=0 ,
得 y3= -8
∴ x =±
√36
= ±6
∴ y =
√-8
3
= -2
①当 x =6, y = -2时,
x + y = 6+(-2)=4
②当 x = -6, y = -2时,
x + y = -6+(-2)= -8
