北师大版七年级下册3.2用关系式表示的变量间关系课件(共19张PPT)
文档属性
| 名称 | 北师大版七年级下册3.2用关系式表示的变量间关系课件(共19张PPT) | 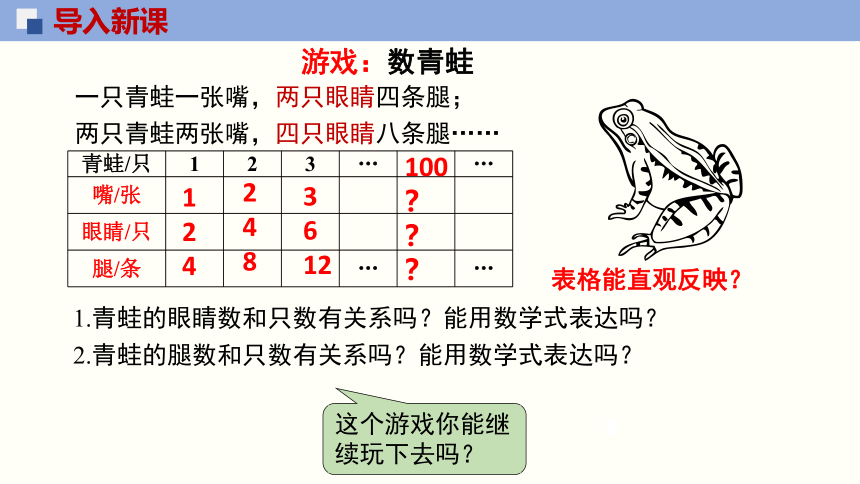 | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 08:33:23 | ||
图片预览






文档简介
(共19张PPT)
导入新课
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
游戏:数青蛙
青蛙/只 1 2 3 … …
嘴/张
眼睛/只
腿/条 … …
1
2
4
24
8
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿……
3
6
12
表格能直观反映?
100
?
?
?
学习目标
知识目标: 1.能根据具体情景,用关系式表示的变量间的关系;
2.并能根据关系式求值,初步体会自变量和因变量的数值对应关系(重点)
能力目标:经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点;(难点)
学科素养:建模思想,数形结合,一一对应
第三章 变量之间的关系
3.2 用关系式表示变量间关系(“式”)
中考考向:关系式是我们学习函数的基础,题型常以选择题、填空题的形式出现;有时会贯穿大题(规律题、应用题、动点问题)的小问进行考查。
知识回顾
在一个变化过程中,主动引起变化的量叫做自变量,
被动引起变化的量叫做因变量,
始终没有变化的量叫做因常量
1.6个月宝宝一天的吃奶情况如下:每天吃x次奶,每次吃150ml,
每天吃奶总量大概在800ml——1000ml,则150ml和x分别是( )
A.常量,变量 B.变量,变量 C.常量,常量 D.变量,常量
2.“早穿皮袄,午穿纱,晚上围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,______随 ______变化而变化,其中在这几个量中________是自变量,_________是因变量.
A
气温
时间
时间
气温
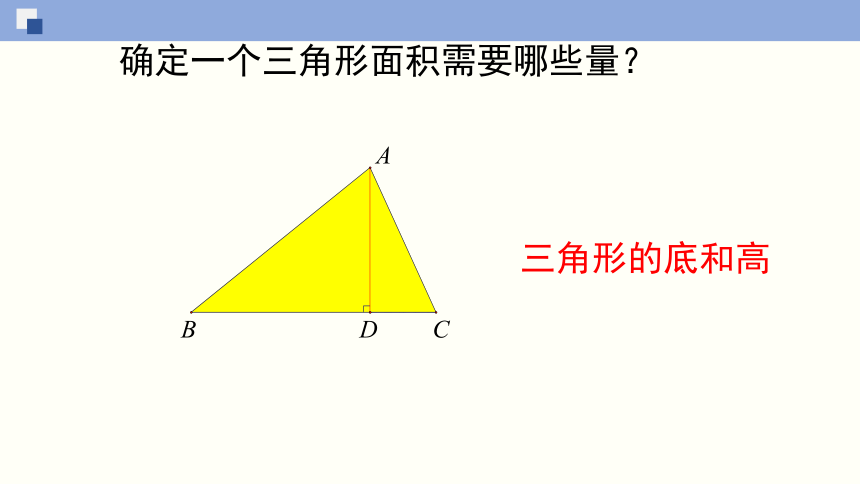
确定一个三角形面积需要哪些量?
D
B
C
A
三角形的底和高
讲授新课
用关系式表示变量间的关系及求值
【例1】如图,△ABC底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
三角形的底边长度,三角形的面积
(2)如果三角形的底边长为x (cm),那么三角形的面积
y (cm2)可以表示为_______.
(3)当底边长从 12 cm变化到 3 cm时,三角形的面积
从______cm2变化到 ______cm2.
y=3x
9
36
知识归纳
1.含义:关系式是我们表示变量之间关系的另一种方法。是指用含有两个变量及数学运算符号的等式来表示的方法;它是用来表示自变量和因变量之间关系的等式。
你能直观地表示这个关系式吗?
y=3x,表示了三角形底边长x 和面积y之间的关系;它是变量y随x变化的关系式。
2.求值:利用关系式,我们可以根据任何一个自变量的值求出相应因变量的值。也可以根据任何一个因变量的值求出相应自变量的值。
解决疑问
1.青蛙的眼睛数和只数有关系吗?能用关系式表达吗?
2.青蛙的腿数和只数有关系吗?能用关系式表达吗?
游戏:数青蛙
若青蛙的眼睛数为y1只,青蛙的只数为n 只,则y1与n的关系式是_______。
若青蛙的腿数为y2只,青蛙的只数为n 只,则y2与n的关系式是_______。
y1=2n
y2=4n
青蛙/只 1 2 3 …
嘴/张
眼睛/只
腿/条 …
1
2
4
24
8
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿……
3
6
12
特别注意
关系式的基本特征是:(书写格式要求)
①等式的左边是因变量,等式的右边是关于自变量、常量的代数式
②等式中只含有自变量和因变量这两个变量,其他的量都是常量
③关系式最后结果要化简,一般不写自变量的取值范围
当堂检测
1. 圆锥的高度是4cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积v(cm3)与r的关系式为 ______________
(3)当底面半径由1cm变化到10cm时,圆锥的体积由 cm3
变化到 cm3 。
圆锥的底面半径
圆锥的体积
h=4
r
(1)在这个变化过程中, 是自变量,
是因变量;
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形,则剩余木板的面积y(m2)与x(m)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
B
3.有一辆汽车储油45升,从某地出发后,每行驶1千米耗油0.1升.若设剩余油量为y(升),行驶的路程为x(千米),则y与x间的关系式为( )
A.y=45-0.1x B.y=45+0.1x C.y=45-x D.y=45+x
A
等量关系:剩余油量=总油量 - 行驶x千米所耗的油量
等量关系:剩余木板面积公式
列关系式的关键:先找出等量关系,然后再把文字换成字母。
4.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下表所示的关系,那么在弹性限度内,弹簧总长y(cm)与所挂重物的质量x(kg)之间的关系式为( )
A.y=x+12 B.y=0.5x+12 C.y=0.5x+10 D.y=x+10.5
x(kg) 0 1 2 3 4 5 6 …
y(cm) 12 12.5 13 13.5 14 14.5 15 …
B
等量关系:弹簧总长度=不挂物体时的弹簧长度+挂物体拉长的长度
总结升华
写两个变量间的关系式常用的等量关系:
(1)利用常见几何图形公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中常见的数量关系,如行程问题中“路程=时间×速度”等;
(3)根据表格与图象中的信息列关系式
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
当堂检测
2.根据程序,计算当输入x=-1时,
输出的结果y是( )
A.-2 B.-1 C.0 D.2
D
3.中国移动在某地的资费标准为包月186元,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸每月电话时长已超出包月总时长,下表是超出部分国内拨打的收费标准:
时间/分 1 2 3 4 5 …
电话费/元 0.36 0.72 1.08 1.44 1.8 …
(1)在这一变化过程中, 是自变量, 是因变量;
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x间的关系式 .
(3)如果打电话超出25分钟,那么这个月小明的爸爸共需付多少电话费?(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
特别提醒
根据关系式求值:
(1)在分段关系式中,必须考虑自变量的范围,只能在允许的范围内任意取值
(2)关系式主要从“式”的角度揭示了两变量间的等量关系,因此,任意知道一个变量的值可以求另一个变量的值。
巩固提升(链接中考)
1.如图,长方形ABCD中,AB=5,AD=3,动点P从点A出发,沿AB、BC边向点C运动(不与C重合);设点P运动的距离为x,△APC的面积为y,如果5<x<8,那么y与x之间的关系式为________.
等量关系:S△APC=S△ABC-S△ABP
变式:去掉“如果5<x<8”,那么y与x之间的关系式为________.
(动点问题)
3.达州市为鼓励居民节约用电,采用分段计费的方法,按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;
月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出当0≤x≤200和x>200时,y与x之间的关系式;
(2)小明家5月份交电费117元,则小明家这个月用电多少度?
(阶梯计费问题)
用关系式表示
变量间的关系
根据关系式求值
含义
根据题意列关系式
已知自变量的值求因变量的值
已知因变量的值求自变量的值
归纳总结,整合提升
课后作业:1、完善相关导学案P23
2、完成练习册P53-54
利用面积、体积、周长公式
根据表格与图象中的信息
利用生活中特定的数量 关系
格式注意:左边是因变量,右边是关于自变量的代数式,其他的量都是常量,结果必须是最简关系式
4. 出生1~6个月的婴儿生长发育得非常快,他们的体重y(g)与月龄x(月)间的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.若一个婴儿出生时的体重是3000 g,则这个婴儿第4个月的体重为( )
A.6000 g B.5800 g C.5000 g D.5100 g
B
3.某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)第______ 年, 年产值是25万元.
y=2x+15
5
导入新课
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
游戏:数青蛙
青蛙/只 1 2 3 … …
嘴/张
眼睛/只
腿/条 … …
1
2
4
24
8
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿……
3
6
12
表格能直观反映?
100
?
?
?
学习目标
知识目标: 1.能根据具体情景,用关系式表示的变量间的关系;
2.并能根据关系式求值,初步体会自变量和因变量的数值对应关系(重点)
能力目标:经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点;(难点)
学科素养:建模思想,数形结合,一一对应
第三章 变量之间的关系
3.2 用关系式表示变量间关系(“式”)
中考考向:关系式是我们学习函数的基础,题型常以选择题、填空题的形式出现;有时会贯穿大题(规律题、应用题、动点问题)的小问进行考查。
知识回顾
在一个变化过程中,主动引起变化的量叫做自变量,
被动引起变化的量叫做因变量,
始终没有变化的量叫做因常量
1.6个月宝宝一天的吃奶情况如下:每天吃x次奶,每次吃150ml,
每天吃奶总量大概在800ml——1000ml,则150ml和x分别是( )
A.常量,变量 B.变量,变量 C.常量,常量 D.变量,常量
2.“早穿皮袄,午穿纱,晚上围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,______随 ______变化而变化,其中在这几个量中________是自变量,_________是因变量.
A
气温
时间
时间
气温
确定一个三角形面积需要哪些量?
D
B
C
A
三角形的底和高
讲授新课
用关系式表示变量间的关系及求值
【例1】如图,△ABC底边BC上的高是6cm,当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?
三角形的底边长度,三角形的面积
(2)如果三角形的底边长为x (cm),那么三角形的面积
y (cm2)可以表示为_______.
(3)当底边长从 12 cm变化到 3 cm时,三角形的面积
从______cm2变化到 ______cm2.
y=3x
9
36
知识归纳
1.含义:关系式是我们表示变量之间关系的另一种方法。是指用含有两个变量及数学运算符号的等式来表示的方法;它是用来表示自变量和因变量之间关系的等式。
你能直观地表示这个关系式吗?
y=3x,表示了三角形底边长x 和面积y之间的关系;它是变量y随x变化的关系式。
2.求值:利用关系式,我们可以根据任何一个自变量的值求出相应因变量的值。也可以根据任何一个因变量的值求出相应自变量的值。
解决疑问
1.青蛙的眼睛数和只数有关系吗?能用关系式表达吗?
2.青蛙的腿数和只数有关系吗?能用关系式表达吗?
游戏:数青蛙
若青蛙的眼睛数为y1只,青蛙的只数为n 只,则y1与n的关系式是_______。
若青蛙的腿数为y2只,青蛙的只数为n 只,则y2与n的关系式是_______。
y1=2n
y2=4n
青蛙/只 1 2 3 …
嘴/张
眼睛/只
腿/条 …
1
2
4
24
8
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿……
3
6
12
特别注意
关系式的基本特征是:(书写格式要求)
①等式的左边是因变量,等式的右边是关于自变量、常量的代数式
②等式中只含有自变量和因变量这两个变量,其他的量都是常量
③关系式最后结果要化简,一般不写自变量的取值范围
当堂检测
1. 圆锥的高度是4cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
(2)如果圆锥底面半径为 r(cm),那么圆锥的体积v(cm3)与r的关系式为 ______________
(3)当底面半径由1cm变化到10cm时,圆锥的体积由 cm3
变化到 cm3 。
圆锥的底面半径
圆锥的体积
h=4
r
(1)在这个变化过程中, 是自变量,
是因变量;
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形,则剩余木板的面积y(m2)与x(m)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
B
3.有一辆汽车储油45升,从某地出发后,每行驶1千米耗油0.1升.若设剩余油量为y(升),行驶的路程为x(千米),则y与x间的关系式为( )
A.y=45-0.1x B.y=45+0.1x C.y=45-x D.y=45+x
A
等量关系:剩余油量=总油量 - 行驶x千米所耗的油量
等量关系:剩余木板面积公式
列关系式的关键:先找出等量关系,然后再把文字换成字母。
4.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下表所示的关系,那么在弹性限度内,弹簧总长y(cm)与所挂重物的质量x(kg)之间的关系式为( )
A.y=x+12 B.y=0.5x+12 C.y=0.5x+10 D.y=x+10.5
x(kg) 0 1 2 3 4 5 6 …
y(cm) 12 12.5 13 13.5 14 14.5 15 …
B
等量关系:弹簧总长度=不挂物体时的弹簧长度+挂物体拉长的长度
总结升华
写两个变量间的关系式常用的等量关系:
(1)利用常见几何图形公式:如图形的周长公式、面积公式、体积公式等;
(2)利用生活中常见的数量关系,如行程问题中“路程=时间×速度”等;
(3)根据表格与图象中的信息列关系式
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
当堂检测
2.根据程序,计算当输入x=-1时,
输出的结果y是( )
A.-2 B.-1 C.0 D.2
D
3.中国移动在某地的资费标准为包月186元,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸每月电话时长已超出包月总时长,下表是超出部分国内拨打的收费标准:
时间/分 1 2 3 4 5 …
电话费/元 0.36 0.72 1.08 1.44 1.8 …
(1)在这一变化过程中, 是自变量, 是因变量;
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x间的关系式 .
(3)如果打电话超出25分钟,那么这个月小明的爸爸共需付多少电话费?(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
特别提醒
根据关系式求值:
(1)在分段关系式中,必须考虑自变量的范围,只能在允许的范围内任意取值
(2)关系式主要从“式”的角度揭示了两变量间的等量关系,因此,任意知道一个变量的值可以求另一个变量的值。
巩固提升(链接中考)
1.如图,长方形ABCD中,AB=5,AD=3,动点P从点A出发,沿AB、BC边向点C运动(不与C重合);设点P运动的距离为x,△APC的面积为y,如果5<x<8,那么y与x之间的关系式为________.
等量关系:S△APC=S△ABC-S△ABP
变式:去掉“如果5<x<8”,那么y与x之间的关系式为________.
(动点问题)
3.达州市为鼓励居民节约用电,采用分段计费的方法,按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;
月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出当0≤x≤200和x>200时,y与x之间的关系式;
(2)小明家5月份交电费117元,则小明家这个月用电多少度?
(阶梯计费问题)
用关系式表示
变量间的关系
根据关系式求值
含义
根据题意列关系式
已知自变量的值求因变量的值
已知因变量的值求自变量的值
归纳总结,整合提升
课后作业:1、完善相关导学案P23
2、完成练习册P53-54
利用面积、体积、周长公式
根据表格与图象中的信息
利用生活中特定的数量 关系
格式注意:左边是因变量,右边是关于自变量的代数式,其他的量都是常量,结果必须是最简关系式
4. 出生1~6个月的婴儿生长发育得非常快,他们的体重y(g)与月龄x(月)间的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.若一个婴儿出生时的体重是3000 g,则这个婴儿第4个月的体重为( )
A.6000 g B.5800 g C.5000 g D.5100 g
B
3.某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)第______ 年, 年产值是25万元.
y=2x+15
5
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
