正弦定理[下学期]
图片预览



文档简介
课件14张PPT。正弦定理猜测:是否对于所有的三角形
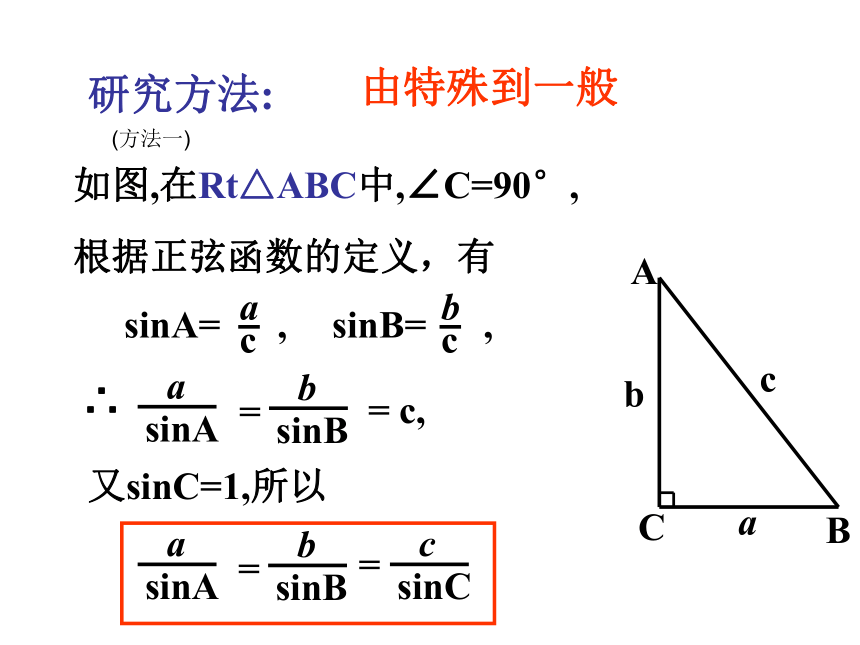
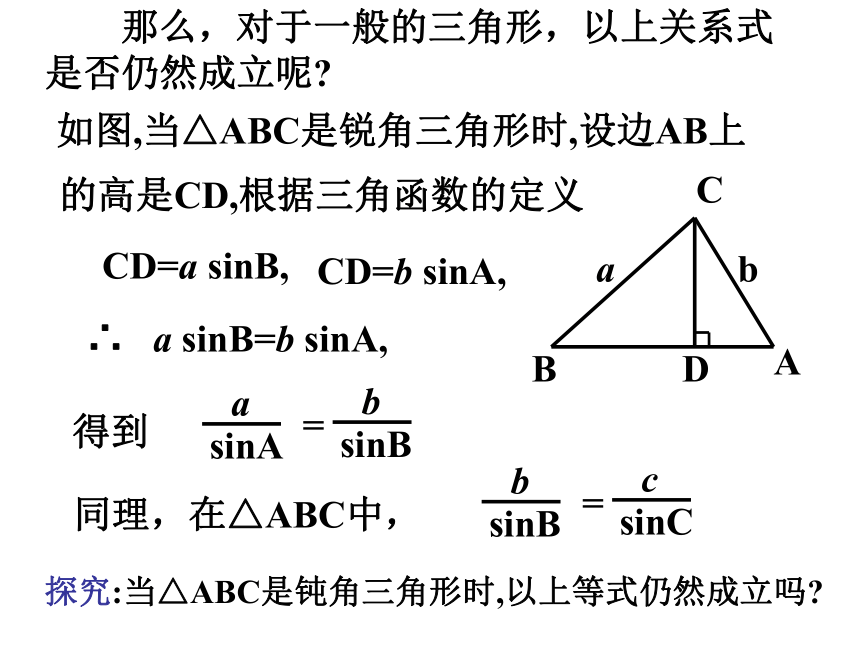
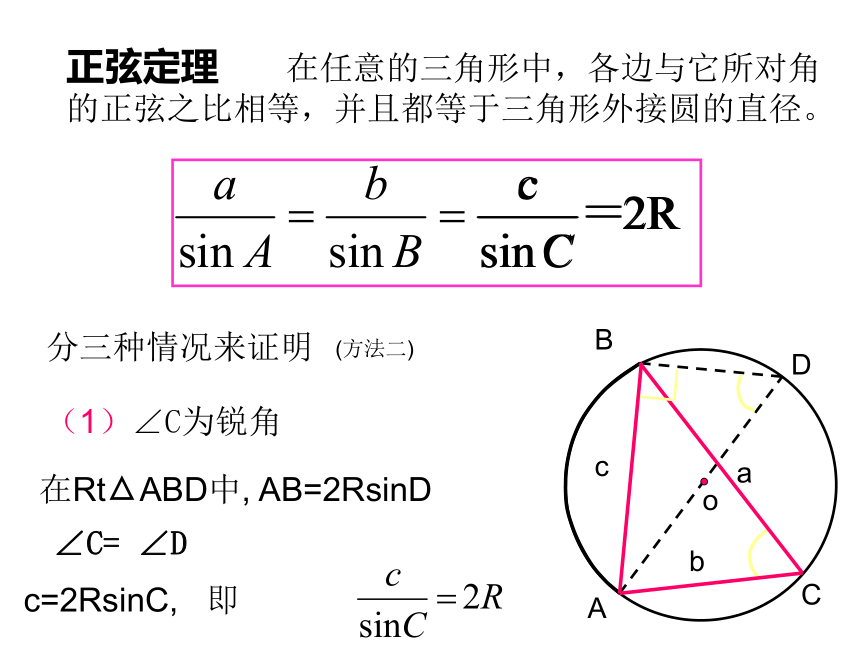
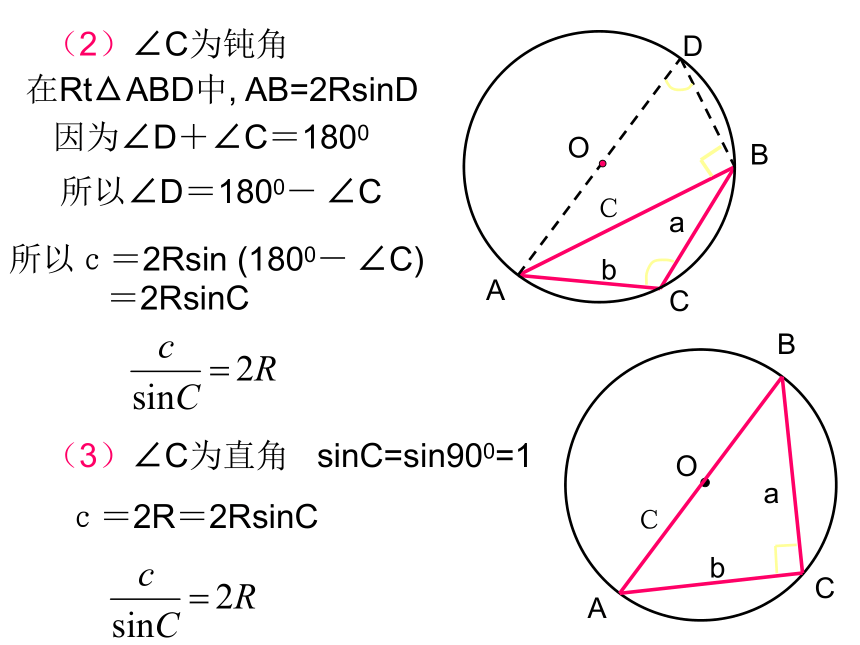
都有 结论成立呢? 观察下列特殊三角形:研究方法:由特殊到一般如图,在Rt△ABC中,∠C=90°,根据正弦函数的定义,有sinA= ,sinB= ,∴== c,又sinC=1,所以==(方法一) 那么,对于一般的三角形,以上关系式是否仍然成立呢?如图,当△ABC是锐角三角形时,设边AB上的高是CD,根据三角函数的定义CD=a sinB,CD=b sinA,∴ a sinB=b sinA,得到同理,在△ABC中,探究:当△ABC是钝角三角形时,以上等式仍然成立吗?正弦定理 在任意的三角形中,各边与它所对角的正弦之比相等,并且都等于三角形外接圆的直径。分三种情况来证明(1)∠C为锐角D c=2RsinC, 即 cba∠C= ∠D(方法二)D(2)∠C为钝角因为∠D+∠C=1800所以∠D=1800- ∠C所以c=2Rsin (1800- ∠C)=2RsinC(3)∠C为直角c=2R=2RsinCsinC=sin900=1同理可证所以方法三:(利用向量知识来证明) 书P6 一般地,把三角形的三个角A、B、C和
它们的对边a、b、c叫做三角形的元素。已知三角形的几个元素求其它元素的过程叫做解三角形.概念介绍思考 我们利用正弦定理可以解
决一些怎样的解三角形的题呢?已知两角和任意一边,可以求出其他两边和一角;
②已知两边和其中一边的对角,可以求出三角形的其他的边和角.例1 如图所示,在 ABC中,已知a=5,∠B=450, ∠C= 1050 ,求∠ A,b,c。cba1050450解:∵ ∠A+∠B+∠C=1800
∴ ∠A = 1800-∠B-∠C
=1800-450-1050 =300由正弦定理得∴≈ =7.07由正弦定理得∴ 而sin1050=sin(1800 -750) =sin750 =0.9659∴≈ =9.659例题2无解练习1小结:
1、用特殊到一般的研究方法证明正弦定理。
它表述了三角形的 边与对角正弦值的关系。
2、定理证明分别从直角、锐角、钝角,运
用分类讨论思想。
3、运用正弦定理求三角形的边和角。Ab作业:课本11页1 2 6
《课课练》
都有 结论成立呢? 观察下列特殊三角形:研究方法:由特殊到一般如图,在Rt△ABC中,∠C=90°,根据正弦函数的定义,有sinA= ,sinB= ,∴== c,又sinC=1,所以==(方法一) 那么,对于一般的三角形,以上关系式是否仍然成立呢?如图,当△ABC是锐角三角形时,设边AB上的高是CD,根据三角函数的定义CD=a sinB,CD=b sinA,∴ a sinB=b sinA,得到同理,在△ABC中,探究:当△ABC是钝角三角形时,以上等式仍然成立吗?正弦定理 在任意的三角形中,各边与它所对角的正弦之比相等,并且都等于三角形外接圆的直径。分三种情况来证明(1)∠C为锐角D c=2RsinC, 即 cba∠C= ∠D(方法二)D(2)∠C为钝角因为∠D+∠C=1800所以∠D=1800- ∠C所以c=2Rsin (1800- ∠C)=2RsinC(3)∠C为直角c=2R=2RsinCsinC=sin900=1同理可证所以方法三:(利用向量知识来证明) 书P6 一般地,把三角形的三个角A、B、C和
它们的对边a、b、c叫做三角形的元素。已知三角形的几个元素求其它元素的过程叫做解三角形.概念介绍思考 我们利用正弦定理可以解
决一些怎样的解三角形的题呢?已知两角和任意一边,可以求出其他两边和一角;
②已知两边和其中一边的对角,可以求出三角形的其他的边和角.例1 如图所示,在 ABC中,已知a=5,∠B=450, ∠C= 1050 ,求∠ A,b,c。cba1050450解:∵ ∠A+∠B+∠C=1800
∴ ∠A = 1800-∠B-∠C
=1800-450-1050 =300由正弦定理得∴≈ =7.07由正弦定理得∴ 而sin1050=sin(1800 -750) =sin750 =0.9659∴≈ =9.659例题2无解练习1小结:
1、用特殊到一般的研究方法证明正弦定理。
它表述了三角形的 边与对角正弦值的关系。
2、定理证明分别从直角、锐角、钝角,运
用分类讨论思想。
3、运用正弦定理求三角形的边和角。Ab作业:课本11页1 2 6
《课课练》
