余弦定理[上学期]
图片预览


文档简介
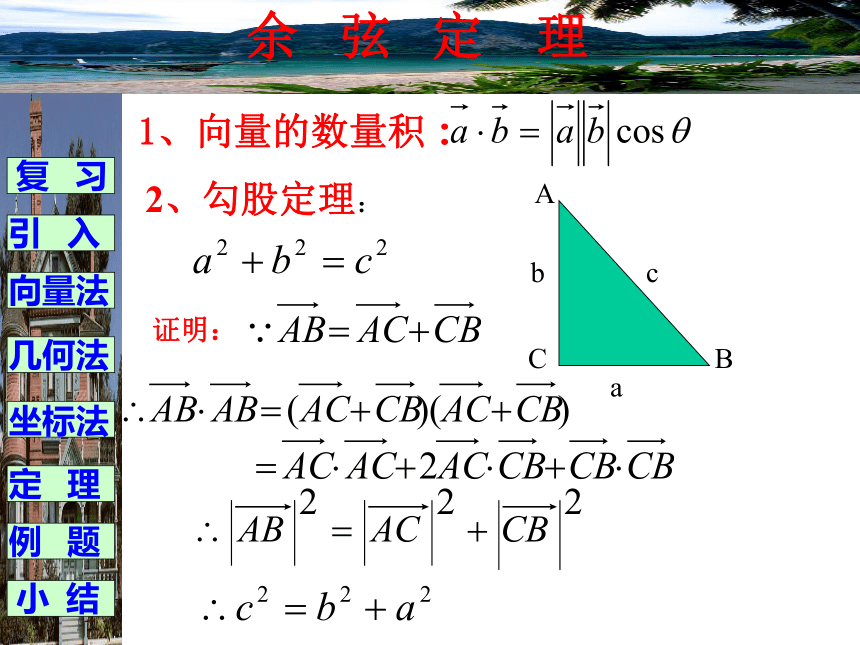
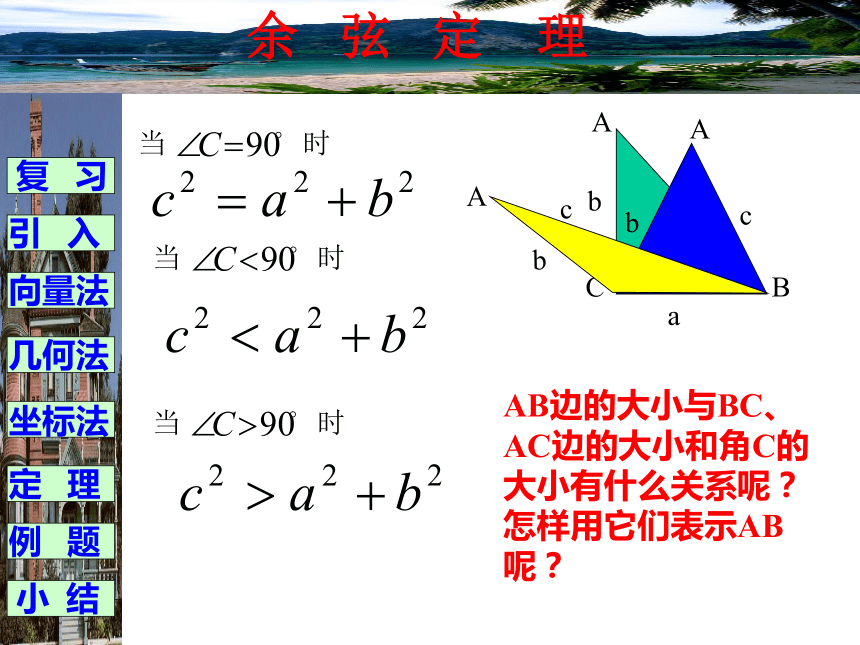
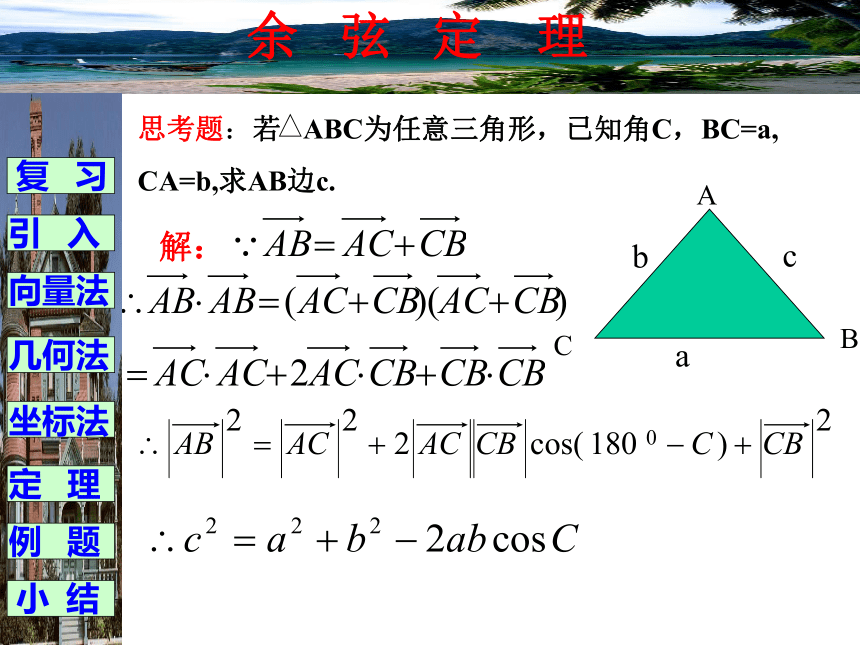
课件12张PPT。余弦定理余 弦 定 理1、向量的数量积:2、勾股定理:证明:复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理当 时当 时当 时AB边的大小与BC、AC边的大小和角C的大小有什么关系呢?怎样用它们表示AB呢?复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理解:复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理定理:三角形任何一边的平方等于其他两边平方的和减 去这两边与它们夹角的余弦的积的两倍。余弦定理可以解决以下两类有关三角形的问题:
(1)已知三边求三个角;
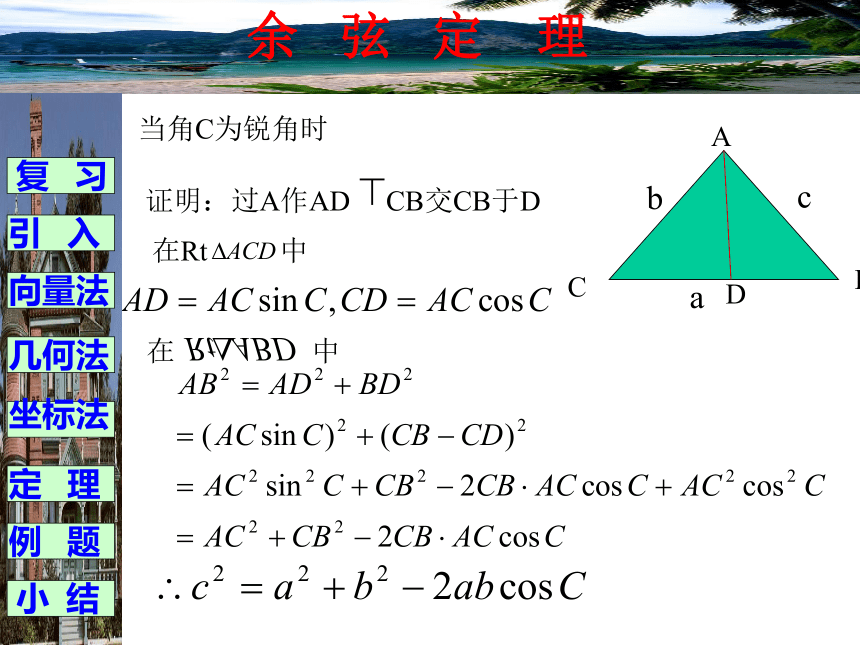
(2)已知两边和它们的夹角,求第三边和其他两个角。复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理D当角C为锐角时证明:过A作AD CB交CB于D在Rt 中在 中复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理当角C为钝角时证明:过A作AD CB交BC的延长线于D在Rt 中在 中D复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理证明:以CB所在的直线为X轴,
过C点垂直于CB的直线为Y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理例题1:在 中例题2:在 中课堂练习:P131,3(1)(2)复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理课堂小结:1、定理:三角形任何一边的平方等于其他两边平方的和减 去这两边与它们夹角的余弦的积的两倍。2、余弦定理可以解决以下两类有关三角形的问题:
(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角。复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理作业:P132:6、8、9复 习引 入向量法几何法坐标法例 题定 理小 结
(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角。复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理D当角C为锐角时证明:过A作AD CB交CB于D在Rt 中在 中复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理当角C为钝角时证明:过A作AD CB交BC的延长线于D在Rt 中在 中D复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理证明:以CB所在的直线为X轴,
过C点垂直于CB的直线为Y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理例题1:在 中例题2:在 中课堂练习:P131,3(1)(2)复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理课堂小结:1、定理:三角形任何一边的平方等于其他两边平方的和减 去这两边与它们夹角的余弦的积的两倍。2、余弦定理可以解决以下两类有关三角形的问题:
(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角。复 习引 入向量法几何法坐标法例 题定 理小 结余 弦 定 理作业:P132:6、8、9复 习引 入向量法几何法坐标法例 题定 理小 结
