湖南省岳阳市岳阳县2021-2022学年八年级下学期期末质量监测数学试题(word版含解析)
文档属性
| 名称 | 湖南省岳阳市岳阳县2021-2022学年八年级下学期期末质量监测数学试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览



文档简介
湖南省岳阳市岳阳县2021-2022 学年八年级下学期期末
质量监测数学试题
一、选择题(每小题 3 分,共 30 分)
1.(3 分)若正比例函数 y=kx 的图象经过点(1,2),则 k 的值为( )
A.﹣ B.﹣2 C. D.2
2.(3 分)在下列所给出坐标的点中在第二象限的是( )
A.(2,3 ) B.(﹣2,3 ) C.(﹣2,﹣3) D.( 2,﹣3) 3.(3 分)在 Rt△ABC 中,∠C=30°,斜边 AC 的长为 5cm,则 AB 的长为( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
4.(3 分)调查某班 30 名同学的跳高成绩时,在收集到的数据中,不足 1.20 米的数出现的频率是 0.82,则达到或超过 1.20 米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
5.(3 分)下列命题中的真命题是( )
A.有一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形D.有一组邻边相等的平行四边形是菱形
6.(3 分)下列长度的三条线段能组成直角三角形的是( )
A.4,5,6 B.2,3,4 C.1,1, D.1,2,2 7.(3 分)已知点 P(2a+4,3a﹣6)在第四象限,那么 a 的取值范围是( )
A.﹣2<a<3 B.a<﹣2 C.a>3 D.﹣2<a<2 8.(3 分)关于 x 的一次函数 y=kx+k2+1 的图象可能正确的是( )
A. B.
C. D.
9.(3 分)如图,已知点 P 到 AE、AD、BC 的距离相等,下列说法:
①点 P 在∠BAC 的平分线上;
②点 P 在∠CBE 的平分线上;
③点 P 在∠BCD 的平分线上;
④点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上. 其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
10.(3 分)如图,矩形 ABCD 中,AB=8,BC=6.点 E 在边 AB 上,点 F 在边 CD 上,点
G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
A.2 B.3 C. D. 二、填空题(每小题 3 分,共 30 分)
11.(3 分)点 P(2,3)关于 x 轴的对称点的坐标为 .
12.(3 分)若直角三角形的一个锐角为 50°,则另一个锐角的度数是 度.
13.(3 分)一个多边形的内角和等于 900°,则它的边数是 .
14.(3 分)若函数 y=2xm+1 是正比例函数,则常数 m 的值是 .
15.(3 分)某班 50 名学生在适应性考试中,分数段在 90~100 分的频率为 0.1,则该班在这个分数段的学生有 人.
16.( 3 分) 已知一个菱形的两条对角线长分别为 6cm 和 8cm , 则这个菱形的面积为
cm2.
17.(3 分)一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,则 k 的取值范围是 .
18.(3 分)把直线 y=﹣2x 向上平移后得到直线 a,直线 a 经过点(m,n),且 2m+n=3,则直线 a 的解析式是 .
19.(3 分)顺次连接四边形 ABCD 各边的中点,得到四边形 EFGH,若四边形 EFGH 是矩
形,则对角线 AC、BD 满足的条件是 .
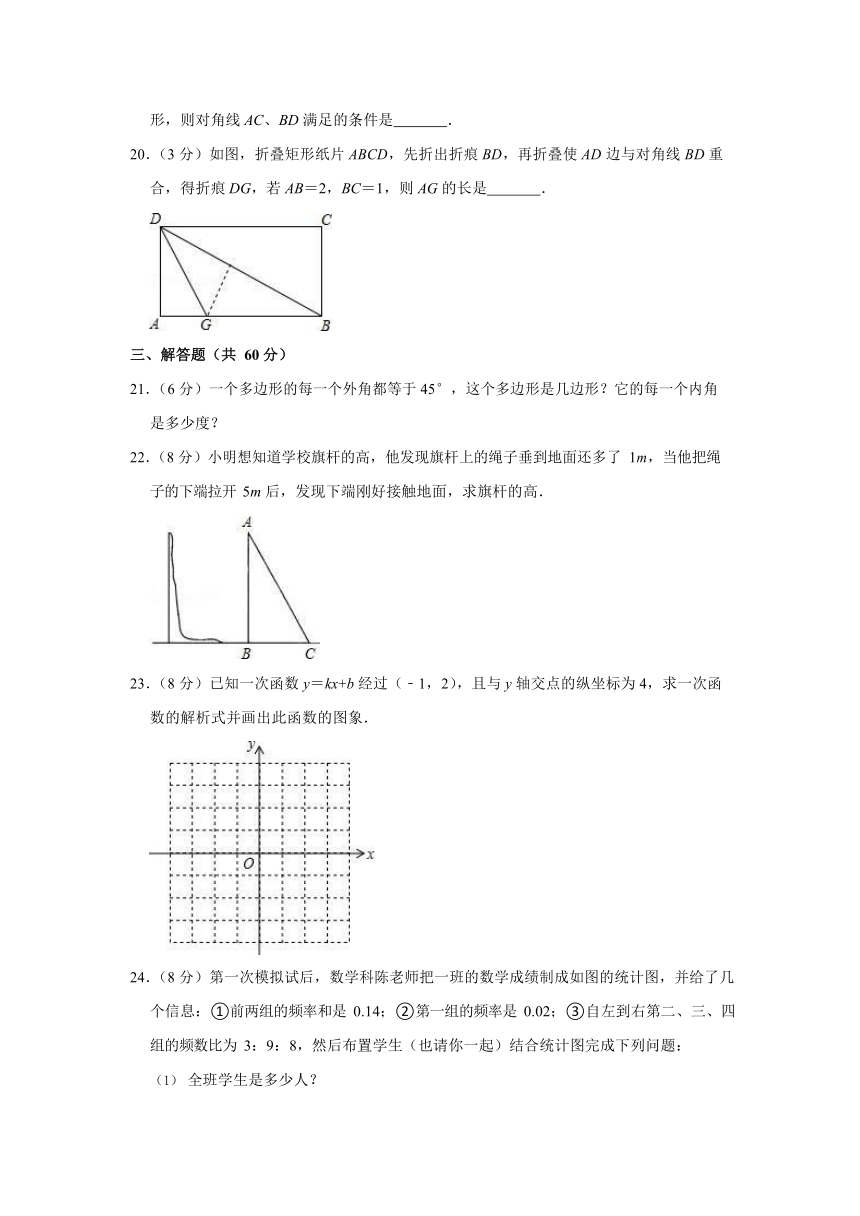
20.(3 分)如图,折叠矩形纸片 ABCD,先折出折痕 BD,再折叠使 AD 边与对角线 BD 重合,得折痕 DG,若 AB=2,BC=1,则 AG 的长是 .
三、解答题(共 60 分)
21.(6 分)一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
22.(8 分)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了 1m,当他把绳子的下端拉开 5m 后,发现下端刚好接触地面,求旗杆的高.
23.(8 分)已知一次函数 y=kx+b 经过(﹣1,2),且与 y 轴交点的纵坐标为 4,求一次函数的解析式并画出此函数的图象.
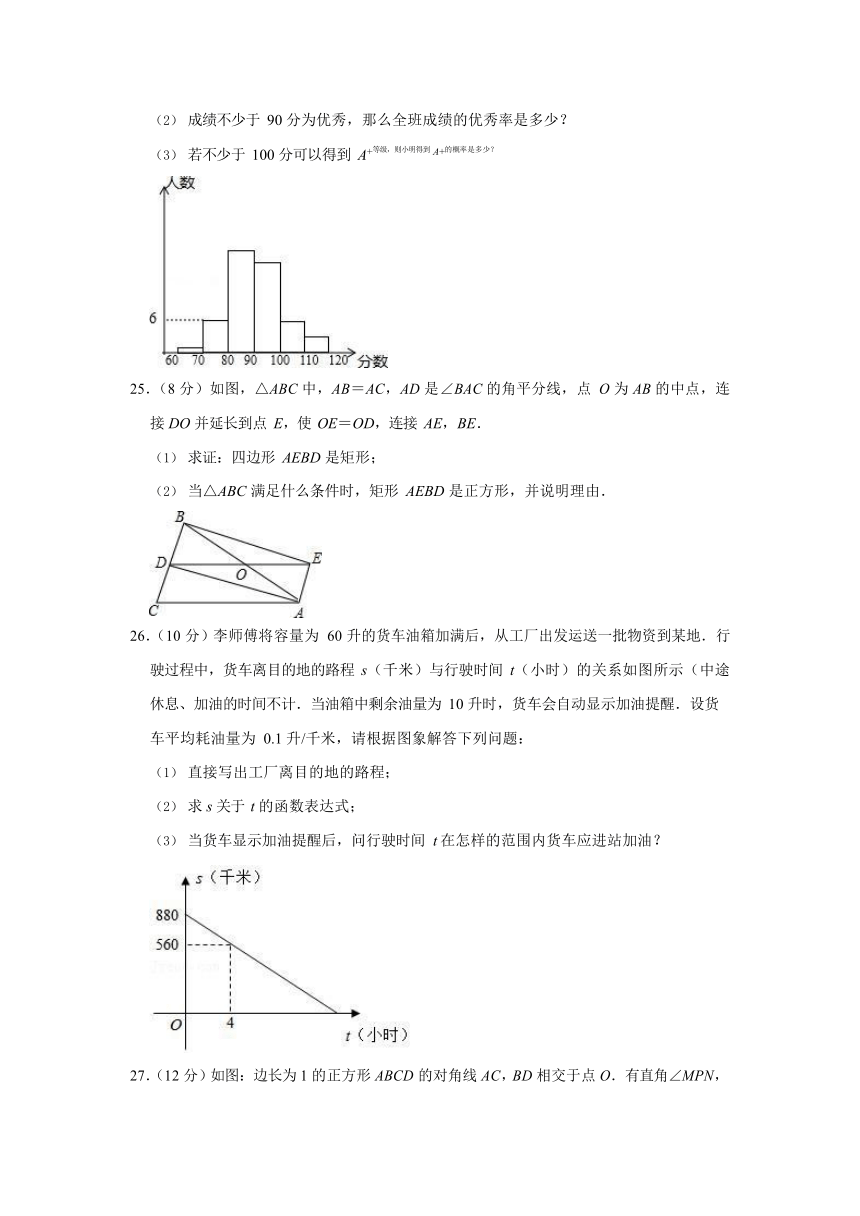
24.(8 分)第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是 0.14;②第一组的频率是 0.02;③自左到右第二、三、四组的频数比为 3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
全班学生是多少人?
成绩不少于 90 分为优秀,那么全班成绩的优秀率是多少?
若不少于 100 分可以得到 A+等级,则小明得到 A+的概率是多少?
25.(8 分)如图,△ABC 中,AB=AC,AD 是∠BAC 的角平分线,点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,连接 AE,BE.
求证:四边形 AEBD 是矩形;
当△ABC 满足什么条件时,矩形 AEBD 是正方形,并说明理由.
26.(10 分)李师傅将容量为 60 升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 s(千米)与行驶时间 t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为 10 升时,货车会自动显示加油提醒.设货
车平均耗油量为 0.1 升/千米,请根据图象解答下列问题:
直接写出工厂离目的地的路程;
求 s 关于 t 的函数表达式;
当货车显示加油提醒后,问行驶时间 t 在怎样的范围内货车应进站加油?
27.(12 分)如图:边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O.有直角∠MPN,
使直角顶点 P 与点 O 重合,直角边 PM,PN 分别与 OA,OB 重合,然后逆时针旋转∠ MPN,旋转角为θ(0o<θ<90o),PM,PN 分别交 AB,BC 于 E,F 两点,连结 EF 交 OB 于点 G.
求证:△BOE≌△COF;
求四边形 OEBF 的面积;
求证:AE2+CF2=2OE2.
湖南省岳阳市岳阳县2021-2022 学年八年级下学期期末质量监测数学试题参考答案与试题解析
一、选择题(每小题 3 分,共 30 分)
1.(3 分)若正比例函数 y=kx 的图象经过点(1,2),则 k 的值为( )
A.﹣ B.﹣2 C. D.2
【分析】把点(1,2)代入已知函数解析式,借助于方程可以求得 k 的值.
【解答】解:∵正比例函数 y=kx 的图象经过点(1,2),
∴2=k,
解得,k=2. 故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.
2.(3 分)在下列所给出坐标的点中在第二象限的是( )
A.(2,3 ) B.(﹣2,3 ) C.(﹣2,﹣3) D.( 2,﹣3)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数解答即可.
【解答】解:∵第二象限内点的横坐标是负数,纵坐标是正数,
∴(2,3)、(﹣2,3)、(﹣2,﹣3)、(2,﹣3)中只有(﹣2,3)在第二象限.故选:B.
【点评】本题考查了点的坐标的知识,解答本题的关键在于记住各象限内点的坐标的符号.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,
﹣);第四象限(+,﹣).
3.(3 分)在 Rt△ABC 中,∠C=30°,斜边 AC 的长为 5cm,则 AB 的长为( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
【分析】由题意可得,∠B 是直角,AB=AC,直接代入即可求得 AB 的长.
【解答】解:∵△ABC 为直角三角形,∠C=30°,
∴AB= AC=2.5cm. 故选:B.
【点评】此题考查的是直角三角形的性质,30°的直角边所对的直角边等于斜边的一半.
4.(3 分)调查某班 30 名同学的跳高成绩时,在收集到的数据中,不足 1.20 米的数出现的频率是 0.82,则达到或超过 1.20 米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
【分析】根据各组的频率之和是 1,进行计算即可解答.
【解答】解:由题意得;
1﹣0.82=0.18,
∴达到或超过 1.20 米的数出现的频率是 0.18, 故选:B.
【点评】本题考查了频数与频率,熟练掌握各组的频率之和是 1 是解题的关键.
5.(3 分)下列命题中的真命题是( ) A.有一组对边平行的四边形是平行四边形B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形D.有一组邻边相等的平行四边形是菱形
【分析】根据平行四边形的判定方法对 A 进行判断;根据矩形的判定方法对 B 进行判断; 根据正方形的判定方法对 C 进行判断;根据菱形的判定方法对 D 进行判断.
【解答】解:A、有两组对边平行的四边形是平行四边形,所以 A 选项错误;
B、有一个角是直角的平行四边形是矩形,所以 B 选项错误;
C、对角线互相垂直平分且相等的四边形是正方形,所以 C 选项错误;
D、有一组邻边相等的平行四边形是菱形,所以 D 选项正确. 故选:D.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
6.(3 分)下列长度的三条线段能组成直角三角形的是( )
A.4,5,6 B.2,3,4 C.1,1, D.1,2,2
【分析】三角形三边满足两个较小边的平方和等于较大边的平方,这个三角形就是直角三角形.
【解答】解:A、52+42≠62,不能作为直角三角形的三边长,故本选项不符合题意.
B、22+32≠42,不能作为直角三角形的三边长,故本选项不符合题意. C、12+12=( )2,能作为直角三角形的三边长,故本选项符合题意. D、12+22≠22,不能作为直角三角形的三边长,故本选项不符合题意. 故选:C.
【点评】本题考查勾股定理的逆定理,关键知道两个较小边的平方和等于较大边的平方, 这个三角形就是直角三角形.
7.(3 分)已知点 P(2a+4,3a﹣6)在第四象限,那么 a 的取值范围是( )
A.﹣2<a<3 B.a<﹣2 C.a>3 D.﹣2<a<2
【分析】根据点在第四象限的条件是:横坐标是正数,纵坐标是负数,把原题转化为解不等式组问题.
【解答】解:∵点 P(2a+4,3a﹣6)在第四象限,
∴ ,
解得:﹣2<a<2, 故选:D.
【点评】坐标平面被两条坐标轴分成了四个象限,每个象限内的点的坐标符号各有特点, 该知识点是中考的常考点,常与不等式、方程结合起来求一些字母的取值范围,比如本题中求 a 的取值范围.
8.(3 分)关于 x 的一次函数 y=kx+k2+1 的图象可能正确的是( )
A. B.
C. D.
【分析】根据图象与 y 轴的交点直接解答即可.
【解答】解:令 x=0,则函数 y=kx+k2+1 的图象与 y 轴交于点(0,k2+1),∵k2+1>0,
∴图象与 y 轴的交点在 y 轴的正半轴上.
故选:C.
【点评】本题考查一次函数的图象,考查学生的分析能力和读图能力.
9.(3 分)如图,已知点 P 到 AE、AD、BC 的距离相等,下列说法:
①点 P 在∠BAC 的平分线上;
②点 P 在∠CBE 的平分线上;
③点 P 在∠BCD 的平分线上;
④点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上. 其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
【分析】根据在角的内部到角的两边距离相等的点在角的平分线上对各小题分析判断即可得解.
【解答】解:∵点 P 到 AE、AD、BC 的距离相等,
∴点 P 在∠BAC 的平分线上,故①正确; 点 P 在∠CBE 的平分线上,故②正确; 点 P 在∠BCD 的平分线上,故③正确;
点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上,故④正确, 综上所述,正确的是①②③④.
故选:A.
【点评】本题考查了角平分线的性质,熟记在角的内部到角的两边距离相等的点在角的平分线上是解题的关键.
10.(3 分)如图,矩形 ABCD 中,AB=8,BC=6.点 E 在边 AB 上,点 F 在边 CD 上,点
G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
A.2 B.3 C. D.
【分析】先连接 EF 交 AC 于 O,由矩形 ABCD 中,四边形 EGFH 是菱形,易证得△CFO
≌△AOE(AAS),即可得 OA=OC,然后由勾股定理求得 AC 的长,继而求得 OA 的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
【解答】解:如图,连接 EF,交 AC 于 O,
∵四边形 EGFH 是菱形,
∴EF⊥AC,OE=OF,
∵四边形 ABCD 是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO 与△AOE 中,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC= =10,
∴AO= AC=5,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴ = ,
∴ = ,
∴AE= . 故选:D.
【点评】此题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角
形的判定与性质,准确作出辅助线是解此题的关键.
二、填空题(每小题 3 分,共 30 分)
11.(3 分)点 P(2,3)关于 x 轴的对称点的坐标为 (2,﹣3) .
【分析】根据关于 x 轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点 P(x, y)关于 x 轴的对称点 P′的坐标是(x,﹣y)得出即可.
【解答】解:∵点 P(2,3)
∴关于 x 轴的对称点的坐标为:(2,﹣3).故答案为:(2,﹣3).
【点评】此题主要考查了关于 x 轴、y 轴对称点的性质,正确记忆坐标规律是解题关键.
12.(3 分)若直角三角形的一个锐角为 50°,则另一个锐角的度数是 40 度.
【分析】根据直角三角形两锐角互余解答.
【解答】解:∵一个锐角为 50°,
∴另一个锐角的度数=90°﹣50°=40°. 故答案为:40°.
【点评】本题利用直角三角形两锐角互余的性质.
13.(3 分)一个多边形的内角和等于 900°,则它的边数是 7 .
【分析】根据 n 边形的内角和为(n﹣2)×180°列出关于 n 的方程式,解方程即可求出边数 n 的值.
【解答】解:设这个多边形的边数是 n, 则:(n﹣2)×180°=900°,
解 得 n=7, 故答案为:7.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,关键在于要根据公式进行正确运算,变形和数据处理.
14.(3 分)若函数 y=2xm+1 是正比例函数,则常数 m 的值是 0 .
【分析】一般地,形如 y=kx(k 是常数,k≠0)的函数叫做正比例函数,依据正比例函数的定义可知,m+1=1,进而得到 m 的值.
【解答】解:∵函数 y=2xm+1 是正比例函数,
∴m+1=1, 解得 m=0,
故答案为:0.
【点评】本题主要考查了正比例函数的定义,正比例函数的定义是从解析式的角度出发的,注意定义中对比例系数的要求:k 是常数,k≠0,k 是正数也可以是负数.
15.(3 分)某班 50 名学生在适应性考试中,分数段在 90~100 分的频率为 0.1,则该班在这个分数段的学生有 5 人.
【分析】由公式:频率= ,得:频数=总人数×频率.
【解答】解:根据题意,得
该班在这个分数段的学生有 50×0.1=5(人).
【点评】能够灵活运用频率= 这一公式是解决本题的关键.
16.(3 分)已知一个菱形的两条对角线长分别为 6cm 和 8cm,则这个菱形的面积为 24 cm2.
【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.
【解答】解:∵一个菱形的两条对角线长分别为 6cm 和 8cm,
∴这个菱形的面积=×6×8=24(cm2).故答案为:24.
【点评】本题考查的是菱形的性质,熟知菱形的面积等于两对角线乘积的一半是解答此题的关键.
17.(3 分)一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,则 k 的取值范围是 0
<k<1 .
【分析】根据一次函数图象与系数的关系得到 k>0 且 k﹣1<0,然后求出两个不等式的公共部分即可.
【解答】解:∵一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,
∴k>0 且 k﹣1<0,
∴0<k<1.
故答案为 0<k<1.
【点评】本题考查了一次函数图象与系数的关系:对于一次函数 y=kx+b,当 k>0,b> 0 y=kx+b 的图象在一、二、三象限;k>0,b<0 y=kx+b 的图象在一、三、四象限; k<0,b>0 y=kx+b 的图象在一、二、四象限;k<0,b<0 y=kx+b 的图象在二、三、四象限.
18.(3 分)把直线 y=﹣2x 向上平移后得到直线 a,直线 a 经过点(m,n),且 2m+n=3,
则直线 a 的解析式是 y=﹣2x+3 .
【分析】根据平移规律“上加下减”得到直线 a 的解析式,然后根据已知条件列出关于
m、n 的方程组,通过解方程组求得系数的值.
【解答】解:设直线 y=﹣2x 向上平移后得到直线 a,则直线 a 的解析式可设为 y=﹣2x+k,把点(m,n)代入得 n=﹣2m+k,则
,
解得 k=3.
∴直线 a 的解析式可设为 y=﹣2x+3. 故答案是:y=﹣2x+3.
【点评】本题考查了一次函数图象与几何变换:一次函数 y=kx+b(k、b 为常数,k≠0) 的图象为直线,当直线平移时 k 不变,当向上平移 m 个单位,则平移后直线的解析式为y=kx+b+m.
19.(3 分)顺次连接四边形 ABCD 各边的中点,得到四边形 EFGH,若四边形 EFGH 是矩形,则对角线 AC、BD 满足的条件是 AC⊥BD .
【分析】根据题意画出相应的图形,如图所示,由四边形 EFGH 为矩形,根据矩形的四个角为直角得到∠FEH=90°,又 EF 为三角形 ABD 的中位线,根据中位线定理得到 EF 与 DB 平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到 EH 与 AC 平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到 AC 与 BD 垂直.
【解答】证明:如图,∵四边形 EFGH 是矩形,
∴∠FEH=90°,
又∵点 E、F、分别是 AD、AB 边的中点,
∴EF 是三角形 ABD 的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点 E、H 分别是 AD、CD 各边的中点,
∴EH 是三角形 ACD 的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即 AC⊥BD.
故答案为:AC⊥BD
【点评】此题考查了矩形的性质,三角形的中位线定理,以及平行线的性质.这类题的一般解法是:借助图形,充分抓住已知条件,找准问题的突破口,由浅入深多角度,多侧面探寻,联想符合题设的有关知识,合理组合发现的新结论,围绕所探结论环环相加, 步步逼近,所探结论便会被“逼出来”.
20.(3 分)如图,折叠矩形纸片 ABCD,先折出折痕 BD,再折叠使 AD 边与对角线 BD 重合,得折痕 DG,若 AB=2,BC=1,则 AG 的长是 .
【分析】已知 AB=2,BC=1,可知 AD=BC=1,在 Rt△ABD 中用勾股定理求 BD;设AG=x,由折叠的性质可知,GH=x,BH=BD﹣DH=BD﹣AD= ﹣1,BG=2﹣x, 在 Rt△BGH 中,用勾股定理列方程求 x 即可.
【解答】解:根据题意:AB=2,AD=BC=1,在 Rt△ABD 中,
BD= = = . 过点 G 作 GH⊥BD,垂足为 H, 由折叠可知:△AGD≌△HGD,
∴AD=DH=1,设 AG 的长为 x,HG=AG=x,BG=2﹣x,BH=﹣1 在 Rt△BGH 中,由勾股定理得 BG2=BH2+HG2,
(2﹣x)2=( ﹣1)2+x2,4﹣4x+x2=5﹣2 +1+x2,
解得 x= ,
即 AG 的长为.
故答案为: .
【点评】本题考查了折叠的性质以及勾股定理等知识,利用折叠性质折叠前后两图形全等,即对应角相等,对应线段相等,对应点的连线段被折痕垂直平分是解题关键.
三、解答题(共 60 分)
21.(6 分)一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
【分析】根据多边形的外角和是 360 度,每个外角都相等,即可求得外角和中外角的个数,即多边形的边数;根据多边形的内角与它相邻的外角互补解答即可.
【解答】解:根据题意,多边形的边数是:360÷45=8, 每一个内角的度数是:180°﹣45°=135°.
故这个多边形是八边形,它的每一个内角是多少度 135°.
【点评】本题主要考查了多边形的内角和定理以及多边形的外角和定理.解题的关键是熟练掌握多边形的内角和定理以及多边形的外角和定理,注意多边形的外角和不随边数的变化而变化,因而把求多边形内角的计算转化为外角的计算,可以使计算简便.
22.(8 分)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了 1m,当他把绳子的下端拉开 5m 后,发现下端刚好接触地面,求旗杆的高.
【分析】根据题意设旗杆的高 AB 为 xm,则绳子 AC 的长为(x+1)m,再利用勾股定理即可求得 AB 的长,即旗杆的高.
【解答】解:设旗杆的高 AB 为 xm,则绳子 AC 的长为(x+1)m 在 Rt△ABC 中,AB2+BC2=AC2
∴x2+52=(x+1)2 解得 x=12
∴AB=12
∴旗杆的高 12m.
【点评】此题考查了学生利用勾股定理解决实际问题的能力.
23.(8 分)已知一次函数 y=kx+b 经过(﹣1,2),且与 y 轴交点的纵坐标为 4,求一次函数的解析式并画出此函数的图象.
【分析】将(﹣1,2)代入一次函数 y=kx+4,求出 k;结合两点确定一条直线作出图形.
【解答】解:依题意可以设该一次函数解析式为 y=kx+4(k≠0).把(﹣1,2)代入得到:2=﹣k+4,
解得 k=2,
所以该函数解析式为:y=2x+4. 其函数图象如图所示:
.
【点评】本题考查了一次函数图象和待定系数法求一次函数解析式.此题属于基础题,
代入求值即可求得系数的值.
24.(8 分)第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是 0.14;②第一组的频率是 0.02;③自左到右第二、三、四组的频数比为 3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
全班学生是多少人?
成绩不少于 90 分为优秀,那么全班成绩的优秀率是多少?
若不少于 100 分可以得到 A+等级,则小明得到 A+的概率是多少?
【分析】(1)首先求得第二组的频率,然后根据第二组的频数是 6,即可求得总人数;
利用 1 减去前三组的频率即可求解;
求得第三、四组的频率,则利用 1 减去前四组的频率即可求解.
【解答】解:(1)第二组的频率是:0.14﹣0.02=0.12,则全班的学生数是:6÷0.12=50;
(2)全班成绩的优秀率是 1﹣0.14﹣0.12×=0.5=50%;
(3)第三、四组的频率是:0.12× =0.68,
则最后两组的频率的和是:1﹣0.14﹣0.68=0.18, 则小明得到 A+的概率是 0.18.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图
获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.(8 分)如图,△ABC 中,AB=AC,AD 是∠BAC 的角平分线,点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,连接 AE,BE.
求证:四边形 AEBD 是矩形;
当△ABC 满足什么条件时,矩形 AEBD 是正方形,并说明理由.
【分析】(1)利用平行四边形的判定首先得出四边形 AEBD 是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出 AD=BD=CD,进而利用正方形的判定得出即可.
【解答】(1)证明:∵点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,
∴四边形 AEBD 是平行四边形,
∵AB=AC,AD 是∠BAC 的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形 AEBD 是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD 是∠BAC 的角平分线,
∴AD=BD=CD,
∵由(1)得四边形 AEBD 是矩形,
∴矩形 AEBD 是正方形.
【点评】此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识, 熟练掌握正方形和矩形的判定是解题关键.
26.(10 分)李师傅将容量为 60 升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 s(千米)与行驶时间 t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为 10 升时,货车会自动显示加油提醒.设货
车平均耗油量为 0.1 升/千米,请根据图象解答下列问题:
直接写出工厂离目的地的路程;
求 s 关于 t 的函数表达式;
当货车显示加油提醒后,问行驶时间 t 在怎样的范围内货车应进站加油?
【分析】(1)由图象直接求出工厂离目的地的路程;
用待定系数法求出函数解析式即可;
当油箱中剩余油量为 10 升时和当油箱中剩余油量为 0 升时,求出 t 的取值即可.
【解答】解:(1)由图象,得 t=0 时,s=880,
∴工厂离目的地的路程为 880 千米,
答:工厂离目的地的路程为 880 千米;
(2)设 s=kt+b(k≠0),
将(0,880)和(4,560)代入 s=kt+b 得,
(
,
解得:
),
∴s 关于 t 的函数表达式:s=﹣80t+880(0≤t≤11), 答:s 关于 t 的函数表达式:s=﹣80t+880(0≤t≤11);
(3)当油箱中剩余油量为 10 升时,
s=880﹣(60﹣10)÷0.1=380(千米),
∴380=﹣80t+880,
解得:t=(小时),
当油箱中剩余油量为 0 升时,
s=880﹣60÷0.1=280(千米),
∴280=﹣80t+880,解得:t=(小时),
∵k=﹣80<0,
∴s 随 t 的增大而减小,
∴t 的取值范围是 ≤t≤ .
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
27.(12 分)如图:边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O.有直角∠MPN,使直角顶点 P 与点 O 重合,直角边 PM,PN 分别与 OA,OB 重合,然后逆时针旋转∠ MPN,旋转角为θ(0o<θ<90o),PM,PN 分别交 AB,BC 于 E,F 两点,连结 EF 交 OB 于点 G.
求证:△BOE≌△COF;
求四边形 OEBF 的面积;
求证:AE2+CF2=2OE2.
【分析】(1)先判断出∠ABO=∠DCO=45°,OB=OC,∠BOC=90°,进而判断出
∠BOE=∠COF,即可判断出结论;
由(1)得出 S△BOE=S△COF,再求出 OB=OC,则可证得结论;
先判断出△OEG∽△OBE,然后由相似三角形的对应边成比例,证得 OG OB=OE2,再利用 OB 与 BD 的关系,OE 与 EF 的关系,即可证得结论.
【解答】(1)证明:∵正方形 ABCD 的对角线 AC,BD 相交于点 O,
∴∠ABO=∠DCO=45°,OB=OC,∠BOC=90°,
∵∠MOP=90°=∠BOC,
∴∠BOE+∠BON=∠COF+∠BON,
∴∠BOE=∠COF, 在△BOE 和△COF 中,
,
∴△BOE≌△COF(ASA);
解:∵边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O,
∴BC=1,OB=OC,∠BOC=90°,
∴OB=OC= ,
由(1)知,△BOE≌△COF,
∴S△BOE=S△COF,
∴S 四边形 OEBF=S△BOE+S△BOF=S△COF+S△BOF=S△BOC=× × = ;
证明:∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OG OB=OE2,
∵OB= BD,OE= EF,
∴OG BD=EF2,
在△BEF 中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
由(1)知,△BOE≌△COF,
∴OE=OF,
在 Rt△EOF 中,EF2=OE2+OF2=2OE2,
∴AE2+CF2=2OE2.
【点评】此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质, 相似三角形的判定和性质,勾股定理,判断出∠BOE=∠COF,是解本题的关键.
质量监测数学试题
一、选择题(每小题 3 分,共 30 分)
1.(3 分)若正比例函数 y=kx 的图象经过点(1,2),则 k 的值为( )
A.﹣ B.﹣2 C. D.2
2.(3 分)在下列所给出坐标的点中在第二象限的是( )
A.(2,3 ) B.(﹣2,3 ) C.(﹣2,﹣3) D.( 2,﹣3) 3.(3 分)在 Rt△ABC 中,∠C=30°,斜边 AC 的长为 5cm,则 AB 的长为( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
4.(3 分)调查某班 30 名同学的跳高成绩时,在收集到的数据中,不足 1.20 米的数出现的频率是 0.82,则达到或超过 1.20 米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
5.(3 分)下列命题中的真命题是( )
A.有一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形D.有一组邻边相等的平行四边形是菱形
6.(3 分)下列长度的三条线段能组成直角三角形的是( )
A.4,5,6 B.2,3,4 C.1,1, D.1,2,2 7.(3 分)已知点 P(2a+4,3a﹣6)在第四象限,那么 a 的取值范围是( )
A.﹣2<a<3 B.a<﹣2 C.a>3 D.﹣2<a<2 8.(3 分)关于 x 的一次函数 y=kx+k2+1 的图象可能正确的是( )
A. B.
C. D.
9.(3 分)如图,已知点 P 到 AE、AD、BC 的距离相等,下列说法:
①点 P 在∠BAC 的平分线上;
②点 P 在∠CBE 的平分线上;
③点 P 在∠BCD 的平分线上;
④点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上. 其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
10.(3 分)如图,矩形 ABCD 中,AB=8,BC=6.点 E 在边 AB 上,点 F 在边 CD 上,点
G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
A.2 B.3 C. D. 二、填空题(每小题 3 分,共 30 分)
11.(3 分)点 P(2,3)关于 x 轴的对称点的坐标为 .
12.(3 分)若直角三角形的一个锐角为 50°,则另一个锐角的度数是 度.
13.(3 分)一个多边形的内角和等于 900°,则它的边数是 .
14.(3 分)若函数 y=2xm+1 是正比例函数,则常数 m 的值是 .
15.(3 分)某班 50 名学生在适应性考试中,分数段在 90~100 分的频率为 0.1,则该班在这个分数段的学生有 人.
16.( 3 分) 已知一个菱形的两条对角线长分别为 6cm 和 8cm , 则这个菱形的面积为
cm2.
17.(3 分)一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,则 k 的取值范围是 .
18.(3 分)把直线 y=﹣2x 向上平移后得到直线 a,直线 a 经过点(m,n),且 2m+n=3,则直线 a 的解析式是 .
19.(3 分)顺次连接四边形 ABCD 各边的中点,得到四边形 EFGH,若四边形 EFGH 是矩
形,则对角线 AC、BD 满足的条件是 .
20.(3 分)如图,折叠矩形纸片 ABCD,先折出折痕 BD,再折叠使 AD 边与对角线 BD 重合,得折痕 DG,若 AB=2,BC=1,则 AG 的长是 .
三、解答题(共 60 分)
21.(6 分)一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
22.(8 分)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了 1m,当他把绳子的下端拉开 5m 后,发现下端刚好接触地面,求旗杆的高.
23.(8 分)已知一次函数 y=kx+b 经过(﹣1,2),且与 y 轴交点的纵坐标为 4,求一次函数的解析式并画出此函数的图象.
24.(8 分)第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是 0.14;②第一组的频率是 0.02;③自左到右第二、三、四组的频数比为 3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
全班学生是多少人?
成绩不少于 90 分为优秀,那么全班成绩的优秀率是多少?
若不少于 100 分可以得到 A+等级,则小明得到 A+的概率是多少?
25.(8 分)如图,△ABC 中,AB=AC,AD 是∠BAC 的角平分线,点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,连接 AE,BE.
求证:四边形 AEBD 是矩形;
当△ABC 满足什么条件时,矩形 AEBD 是正方形,并说明理由.
26.(10 分)李师傅将容量为 60 升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 s(千米)与行驶时间 t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为 10 升时,货车会自动显示加油提醒.设货
车平均耗油量为 0.1 升/千米,请根据图象解答下列问题:
直接写出工厂离目的地的路程;
求 s 关于 t 的函数表达式;
当货车显示加油提醒后,问行驶时间 t 在怎样的范围内货车应进站加油?
27.(12 分)如图:边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O.有直角∠MPN,
使直角顶点 P 与点 O 重合,直角边 PM,PN 分别与 OA,OB 重合,然后逆时针旋转∠ MPN,旋转角为θ(0o<θ<90o),PM,PN 分别交 AB,BC 于 E,F 两点,连结 EF 交 OB 于点 G.
求证:△BOE≌△COF;
求四边形 OEBF 的面积;
求证:AE2+CF2=2OE2.
湖南省岳阳市岳阳县2021-2022 学年八年级下学期期末质量监测数学试题参考答案与试题解析
一、选择题(每小题 3 分,共 30 分)
1.(3 分)若正比例函数 y=kx 的图象经过点(1,2),则 k 的值为( )
A.﹣ B.﹣2 C. D.2
【分析】把点(1,2)代入已知函数解析式,借助于方程可以求得 k 的值.
【解答】解:∵正比例函数 y=kx 的图象经过点(1,2),
∴2=k,
解得,k=2. 故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.
2.(3 分)在下列所给出坐标的点中在第二象限的是( )
A.(2,3 ) B.(﹣2,3 ) C.(﹣2,﹣3) D.( 2,﹣3)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数解答即可.
【解答】解:∵第二象限内点的横坐标是负数,纵坐标是正数,
∴(2,3)、(﹣2,3)、(﹣2,﹣3)、(2,﹣3)中只有(﹣2,3)在第二象限.故选:B.
【点评】本题考查了点的坐标的知识,解答本题的关键在于记住各象限内点的坐标的符号.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,
﹣);第四象限(+,﹣).
3.(3 分)在 Rt△ABC 中,∠C=30°,斜边 AC 的长为 5cm,则 AB 的长为( )
A.2 cm B.2.5 cm C.3 cm D.4 cm
【分析】由题意可得,∠B 是直角,AB=AC,直接代入即可求得 AB 的长.
【解答】解:∵△ABC 为直角三角形,∠C=30°,
∴AB= AC=2.5cm. 故选:B.
【点评】此题考查的是直角三角形的性质,30°的直角边所对的直角边等于斜边的一半.
4.(3 分)调查某班 30 名同学的跳高成绩时,在收集到的数据中,不足 1.20 米的数出现的频率是 0.82,则达到或超过 1.20 米的数出现的频率是( )
A.0.82 B.0.18 C.30 D.1
【分析】根据各组的频率之和是 1,进行计算即可解答.
【解答】解:由题意得;
1﹣0.82=0.18,
∴达到或超过 1.20 米的数出现的频率是 0.18, 故选:B.
【点评】本题考查了频数与频率,熟练掌握各组的频率之和是 1 是解题的关键.
5.(3 分)下列命题中的真命题是( ) A.有一组对边平行的四边形是平行四边形B.有一个角是直角的四边形是矩形
C.对角线互相垂直平分的四边形是正方形D.有一组邻边相等的平行四边形是菱形
【分析】根据平行四边形的判定方法对 A 进行判断;根据矩形的判定方法对 B 进行判断; 根据正方形的判定方法对 C 进行判断;根据菱形的判定方法对 D 进行判断.
【解答】解:A、有两组对边平行的四边形是平行四边形,所以 A 选项错误;
B、有一个角是直角的平行四边形是矩形,所以 B 选项错误;
C、对角线互相垂直平分且相等的四边形是正方形,所以 C 选项错误;
D、有一组邻边相等的平行四边形是菱形,所以 D 选项正确. 故选:D.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
6.(3 分)下列长度的三条线段能组成直角三角形的是( )
A.4,5,6 B.2,3,4 C.1,1, D.1,2,2
【分析】三角形三边满足两个较小边的平方和等于较大边的平方,这个三角形就是直角三角形.
【解答】解:A、52+42≠62,不能作为直角三角形的三边长,故本选项不符合题意.
B、22+32≠42,不能作为直角三角形的三边长,故本选项不符合题意. C、12+12=( )2,能作为直角三角形的三边长,故本选项符合题意. D、12+22≠22,不能作为直角三角形的三边长,故本选项不符合题意. 故选:C.
【点评】本题考查勾股定理的逆定理,关键知道两个较小边的平方和等于较大边的平方, 这个三角形就是直角三角形.
7.(3 分)已知点 P(2a+4,3a﹣6)在第四象限,那么 a 的取值范围是( )
A.﹣2<a<3 B.a<﹣2 C.a>3 D.﹣2<a<2
【分析】根据点在第四象限的条件是:横坐标是正数,纵坐标是负数,把原题转化为解不等式组问题.
【解答】解:∵点 P(2a+4,3a﹣6)在第四象限,
∴ ,
解得:﹣2<a<2, 故选:D.
【点评】坐标平面被两条坐标轴分成了四个象限,每个象限内的点的坐标符号各有特点, 该知识点是中考的常考点,常与不等式、方程结合起来求一些字母的取值范围,比如本题中求 a 的取值范围.
8.(3 分)关于 x 的一次函数 y=kx+k2+1 的图象可能正确的是( )
A. B.
C. D.
【分析】根据图象与 y 轴的交点直接解答即可.
【解答】解:令 x=0,则函数 y=kx+k2+1 的图象与 y 轴交于点(0,k2+1),∵k2+1>0,
∴图象与 y 轴的交点在 y 轴的正半轴上.
故选:C.
【点评】本题考查一次函数的图象,考查学生的分析能力和读图能力.
9.(3 分)如图,已知点 P 到 AE、AD、BC 的距离相等,下列说法:
①点 P 在∠BAC 的平分线上;
②点 P 在∠CBE 的平分线上;
③点 P 在∠BCD 的平分线上;
④点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上. 其中正确的是( )
A.①②③④ B.①②③ C.④ D.②③
【分析】根据在角的内部到角的两边距离相等的点在角的平分线上对各小题分析判断即可得解.
【解答】解:∵点 P 到 AE、AD、BC 的距离相等,
∴点 P 在∠BAC 的平分线上,故①正确; 点 P 在∠CBE 的平分线上,故②正确; 点 P 在∠BCD 的平分线上,故③正确;
点 P 在∠BAC,∠CBE,∠BCD 的平分线的交点上,故④正确, 综上所述,正确的是①②③④.
故选:A.
【点评】本题考查了角平分线的性质,熟记在角的内部到角的两边距离相等的点在角的平分线上是解题的关键.
10.(3 分)如图,矩形 ABCD 中,AB=8,BC=6.点 E 在边 AB 上,点 F 在边 CD 上,点
G、H 在对角线 AC 上.若四边形 EGFH 是菱形,则 AE 的长是( )
A.2 B.3 C. D.
【分析】先连接 EF 交 AC 于 O,由矩形 ABCD 中,四边形 EGFH 是菱形,易证得△CFO
≌△AOE(AAS),即可得 OA=OC,然后由勾股定理求得 AC 的长,继而求得 OA 的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
【解答】解:如图,连接 EF,交 AC 于 O,
∵四边形 EGFH 是菱形,
∴EF⊥AC,OE=OF,
∵四边形 ABCD 是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO 与△AOE 中,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC= =10,
∴AO= AC=5,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴ = ,
∴ = ,
∴AE= . 故选:D.
【点评】此题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角
形的判定与性质,准确作出辅助线是解此题的关键.
二、填空题(每小题 3 分,共 30 分)
11.(3 分)点 P(2,3)关于 x 轴的对称点的坐标为 (2,﹣3) .
【分析】根据关于 x 轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点 P(x, y)关于 x 轴的对称点 P′的坐标是(x,﹣y)得出即可.
【解答】解:∵点 P(2,3)
∴关于 x 轴的对称点的坐标为:(2,﹣3).故答案为:(2,﹣3).
【点评】此题主要考查了关于 x 轴、y 轴对称点的性质,正确记忆坐标规律是解题关键.
12.(3 分)若直角三角形的一个锐角为 50°,则另一个锐角的度数是 40 度.
【分析】根据直角三角形两锐角互余解答.
【解答】解:∵一个锐角为 50°,
∴另一个锐角的度数=90°﹣50°=40°. 故答案为:40°.
【点评】本题利用直角三角形两锐角互余的性质.
13.(3 分)一个多边形的内角和等于 900°,则它的边数是 7 .
【分析】根据 n 边形的内角和为(n﹣2)×180°列出关于 n 的方程式,解方程即可求出边数 n 的值.
【解答】解:设这个多边形的边数是 n, 则:(n﹣2)×180°=900°,
解 得 n=7, 故答案为:7.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,关键在于要根据公式进行正确运算,变形和数据处理.
14.(3 分)若函数 y=2xm+1 是正比例函数,则常数 m 的值是 0 .
【分析】一般地,形如 y=kx(k 是常数,k≠0)的函数叫做正比例函数,依据正比例函数的定义可知,m+1=1,进而得到 m 的值.
【解答】解:∵函数 y=2xm+1 是正比例函数,
∴m+1=1, 解得 m=0,
故答案为:0.
【点评】本题主要考查了正比例函数的定义,正比例函数的定义是从解析式的角度出发的,注意定义中对比例系数的要求:k 是常数,k≠0,k 是正数也可以是负数.
15.(3 分)某班 50 名学生在适应性考试中,分数段在 90~100 分的频率为 0.1,则该班在这个分数段的学生有 5 人.
【分析】由公式:频率= ,得:频数=总人数×频率.
【解答】解:根据题意,得
该班在这个分数段的学生有 50×0.1=5(人).
【点评】能够灵活运用频率= 这一公式是解决本题的关键.
16.(3 分)已知一个菱形的两条对角线长分别为 6cm 和 8cm,则这个菱形的面积为 24 cm2.
【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.
【解答】解:∵一个菱形的两条对角线长分别为 6cm 和 8cm,
∴这个菱形的面积=×6×8=24(cm2).故答案为:24.
【点评】本题考查的是菱形的性质,熟知菱形的面积等于两对角线乘积的一半是解答此题的关键.
17.(3 分)一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,则 k 的取值范围是 0
<k<1 .
【分析】根据一次函数图象与系数的关系得到 k>0 且 k﹣1<0,然后求出两个不等式的公共部分即可.
【解答】解:∵一次函数 y=kx+(k﹣1)的图象经过第一、三、四象限,
∴k>0 且 k﹣1<0,
∴0<k<1.
故答案为 0<k<1.
【点评】本题考查了一次函数图象与系数的关系:对于一次函数 y=kx+b,当 k>0,b> 0 y=kx+b 的图象在一、二、三象限;k>0,b<0 y=kx+b 的图象在一、三、四象限; k<0,b>0 y=kx+b 的图象在一、二、四象限;k<0,b<0 y=kx+b 的图象在二、三、四象限.
18.(3 分)把直线 y=﹣2x 向上平移后得到直线 a,直线 a 经过点(m,n),且 2m+n=3,
则直线 a 的解析式是 y=﹣2x+3 .
【分析】根据平移规律“上加下减”得到直线 a 的解析式,然后根据已知条件列出关于
m、n 的方程组,通过解方程组求得系数的值.
【解答】解:设直线 y=﹣2x 向上平移后得到直线 a,则直线 a 的解析式可设为 y=﹣2x+k,把点(m,n)代入得 n=﹣2m+k,则
,
解得 k=3.
∴直线 a 的解析式可设为 y=﹣2x+3. 故答案是:y=﹣2x+3.
【点评】本题考查了一次函数图象与几何变换:一次函数 y=kx+b(k、b 为常数,k≠0) 的图象为直线,当直线平移时 k 不变,当向上平移 m 个单位,则平移后直线的解析式为y=kx+b+m.
19.(3 分)顺次连接四边形 ABCD 各边的中点,得到四边形 EFGH,若四边形 EFGH 是矩形,则对角线 AC、BD 满足的条件是 AC⊥BD .
【分析】根据题意画出相应的图形,如图所示,由四边形 EFGH 为矩形,根据矩形的四个角为直角得到∠FEH=90°,又 EF 为三角形 ABD 的中位线,根据中位线定理得到 EF 与 DB 平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到 EH 与 AC 平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到 AC 与 BD 垂直.
【解答】证明:如图,∵四边形 EFGH 是矩形,
∴∠FEH=90°,
又∵点 E、F、分别是 AD、AB 边的中点,
∴EF 是三角形 ABD 的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点 E、H 分别是 AD、CD 各边的中点,
∴EH 是三角形 ACD 的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即 AC⊥BD.
故答案为:AC⊥BD
【点评】此题考查了矩形的性质,三角形的中位线定理,以及平行线的性质.这类题的一般解法是:借助图形,充分抓住已知条件,找准问题的突破口,由浅入深多角度,多侧面探寻,联想符合题设的有关知识,合理组合发现的新结论,围绕所探结论环环相加, 步步逼近,所探结论便会被“逼出来”.
20.(3 分)如图,折叠矩形纸片 ABCD,先折出折痕 BD,再折叠使 AD 边与对角线 BD 重合,得折痕 DG,若 AB=2,BC=1,则 AG 的长是 .
【分析】已知 AB=2,BC=1,可知 AD=BC=1,在 Rt△ABD 中用勾股定理求 BD;设AG=x,由折叠的性质可知,GH=x,BH=BD﹣DH=BD﹣AD= ﹣1,BG=2﹣x, 在 Rt△BGH 中,用勾股定理列方程求 x 即可.
【解答】解:根据题意:AB=2,AD=BC=1,在 Rt△ABD 中,
BD= = = . 过点 G 作 GH⊥BD,垂足为 H, 由折叠可知:△AGD≌△HGD,
∴AD=DH=1,设 AG 的长为 x,HG=AG=x,BG=2﹣x,BH=﹣1 在 Rt△BGH 中,由勾股定理得 BG2=BH2+HG2,
(2﹣x)2=( ﹣1)2+x2,4﹣4x+x2=5﹣2 +1+x2,
解得 x= ,
即 AG 的长为.
故答案为: .
【点评】本题考查了折叠的性质以及勾股定理等知识,利用折叠性质折叠前后两图形全等,即对应角相等,对应线段相等,对应点的连线段被折痕垂直平分是解题关键.
三、解答题(共 60 分)
21.(6 分)一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
【分析】根据多边形的外角和是 360 度,每个外角都相等,即可求得外角和中外角的个数,即多边形的边数;根据多边形的内角与它相邻的外角互补解答即可.
【解答】解:根据题意,多边形的边数是:360÷45=8, 每一个内角的度数是:180°﹣45°=135°.
故这个多边形是八边形,它的每一个内角是多少度 135°.
【点评】本题主要考查了多边形的内角和定理以及多边形的外角和定理.解题的关键是熟练掌握多边形的内角和定理以及多边形的外角和定理,注意多边形的外角和不随边数的变化而变化,因而把求多边形内角的计算转化为外角的计算,可以使计算简便.
22.(8 分)小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多了 1m,当他把绳子的下端拉开 5m 后,发现下端刚好接触地面,求旗杆的高.
【分析】根据题意设旗杆的高 AB 为 xm,则绳子 AC 的长为(x+1)m,再利用勾股定理即可求得 AB 的长,即旗杆的高.
【解答】解:设旗杆的高 AB 为 xm,则绳子 AC 的长为(x+1)m 在 Rt△ABC 中,AB2+BC2=AC2
∴x2+52=(x+1)2 解得 x=12
∴AB=12
∴旗杆的高 12m.
【点评】此题考查了学生利用勾股定理解决实际问题的能力.
23.(8 分)已知一次函数 y=kx+b 经过(﹣1,2),且与 y 轴交点的纵坐标为 4,求一次函数的解析式并画出此函数的图象.
【分析】将(﹣1,2)代入一次函数 y=kx+4,求出 k;结合两点确定一条直线作出图形.
【解答】解:依题意可以设该一次函数解析式为 y=kx+4(k≠0).把(﹣1,2)代入得到:2=﹣k+4,
解得 k=2,
所以该函数解析式为:y=2x+4. 其函数图象如图所示:
.
【点评】本题考查了一次函数图象和待定系数法求一次函数解析式.此题属于基础题,
代入求值即可求得系数的值.
24.(8 分)第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是 0.14;②第一组的频率是 0.02;③自左到右第二、三、四组的频数比为 3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题:
全班学生是多少人?
成绩不少于 90 分为优秀,那么全班成绩的优秀率是多少?
若不少于 100 分可以得到 A+等级,则小明得到 A+的概率是多少?
【分析】(1)首先求得第二组的频率,然后根据第二组的频数是 6,即可求得总人数;
利用 1 减去前三组的频率即可求解;
求得第三、四组的频率,则利用 1 减去前四组的频率即可求解.
【解答】解:(1)第二组的频率是:0.14﹣0.02=0.12,则全班的学生数是:6÷0.12=50;
(2)全班成绩的优秀率是 1﹣0.14﹣0.12×=0.5=50%;
(3)第三、四组的频率是:0.12× =0.68,
则最后两组的频率的和是:1﹣0.14﹣0.68=0.18, 则小明得到 A+的概率是 0.18.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图
获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.(8 分)如图,△ABC 中,AB=AC,AD 是∠BAC 的角平分线,点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,连接 AE,BE.
求证:四边形 AEBD 是矩形;
当△ABC 满足什么条件时,矩形 AEBD 是正方形,并说明理由.
【分析】(1)利用平行四边形的判定首先得出四边形 AEBD 是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出 AD=BD=CD,进而利用正方形的判定得出即可.
【解答】(1)证明:∵点 O 为 AB 的中点,连接 DO 并延长到点 E,使 OE=OD,
∴四边形 AEBD 是平行四边形,
∵AB=AC,AD 是∠BAC 的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形 AEBD 是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD 是∠BAC 的角平分线,
∴AD=BD=CD,
∵由(1)得四边形 AEBD 是矩形,
∴矩形 AEBD 是正方形.
【点评】此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识, 熟练掌握正方形和矩形的判定是解题关键.
26.(10 分)李师傅将容量为 60 升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 s(千米)与行驶时间 t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为 10 升时,货车会自动显示加油提醒.设货
车平均耗油量为 0.1 升/千米,请根据图象解答下列问题:
直接写出工厂离目的地的路程;
求 s 关于 t 的函数表达式;
当货车显示加油提醒后,问行驶时间 t 在怎样的范围内货车应进站加油?
【分析】(1)由图象直接求出工厂离目的地的路程;
用待定系数法求出函数解析式即可;
当油箱中剩余油量为 10 升时和当油箱中剩余油量为 0 升时,求出 t 的取值即可.
【解答】解:(1)由图象,得 t=0 时,s=880,
∴工厂离目的地的路程为 880 千米,
答:工厂离目的地的路程为 880 千米;
(2)设 s=kt+b(k≠0),
将(0,880)和(4,560)代入 s=kt+b 得,
(
,
解得:
),
∴s 关于 t 的函数表达式:s=﹣80t+880(0≤t≤11), 答:s 关于 t 的函数表达式:s=﹣80t+880(0≤t≤11);
(3)当油箱中剩余油量为 10 升时,
s=880﹣(60﹣10)÷0.1=380(千米),
∴380=﹣80t+880,
解得:t=(小时),
当油箱中剩余油量为 0 升时,
s=880﹣60÷0.1=280(千米),
∴280=﹣80t+880,解得:t=(小时),
∵k=﹣80<0,
∴s 随 t 的增大而减小,
∴t 的取值范围是 ≤t≤ .
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
27.(12 分)如图:边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O.有直角∠MPN,使直角顶点 P 与点 O 重合,直角边 PM,PN 分别与 OA,OB 重合,然后逆时针旋转∠ MPN,旋转角为θ(0o<θ<90o),PM,PN 分别交 AB,BC 于 E,F 两点,连结 EF 交 OB 于点 G.
求证:△BOE≌△COF;
求四边形 OEBF 的面积;
求证:AE2+CF2=2OE2.
【分析】(1)先判断出∠ABO=∠DCO=45°,OB=OC,∠BOC=90°,进而判断出
∠BOE=∠COF,即可判断出结论;
由(1)得出 S△BOE=S△COF,再求出 OB=OC,则可证得结论;
先判断出△OEG∽△OBE,然后由相似三角形的对应边成比例,证得 OG OB=OE2,再利用 OB 与 BD 的关系,OE 与 EF 的关系,即可证得结论.
【解答】(1)证明:∵正方形 ABCD 的对角线 AC,BD 相交于点 O,
∴∠ABO=∠DCO=45°,OB=OC,∠BOC=90°,
∵∠MOP=90°=∠BOC,
∴∠BOE+∠BON=∠COF+∠BON,
∴∠BOE=∠COF, 在△BOE 和△COF 中,
,
∴△BOE≌△COF(ASA);
解:∵边长为 1 的正方形 ABCD 的对角线 AC,BD 相交于点 O,
∴BC=1,OB=OC,∠BOC=90°,
∴OB=OC= ,
由(1)知,△BOE≌△COF,
∴S△BOE=S△COF,
∴S 四边形 OEBF=S△BOE+S△BOF=S△COF+S△BOF=S△BOC=× × = ;
证明:∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OG OB=OE2,
∵OB= BD,OE= EF,
∴OG BD=EF2,
在△BEF 中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
由(1)知,△BOE≌△COF,
∴OE=OF,
在 Rt△EOF 中,EF2=OE2+OF2=2OE2,
∴AE2+CF2=2OE2.
【点评】此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质, 相似三角形的判定和性质,勾股定理,判断出∠BOE=∠COF,是解本题的关键.
同课章节目录
