§3.3.1函数的单调性与导数 课件(共19张PPT)
文档属性
| 名称 | §3.3.1函数的单调性与导数 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 11:07:57 | ||
图片预览





文档简介
(共19张PPT)
过山车是一项富有刺激性的娱乐工具。那种风驰电掣、有惊无险的感觉令不少人着迷。
复习引入:
1、导数的定义
导数的几何意义
函数在一点处的导数,就是对应的函数图像在该点的切线的斜率。
复习引入:
2、函数的单调性的定义
对于给定区间上的函数f(x),如果对于属于这个区间的任意两个自变量的值x1,x2,
当x1那么f(x)在这个区间上是增函数.
.
即x1-x2与f(x1)-f(x2)同号,即
当x1f (x2),
那么f(x)在这个区间上是减函数
此时x1-x2与f(x1)-f(x2)异号,即
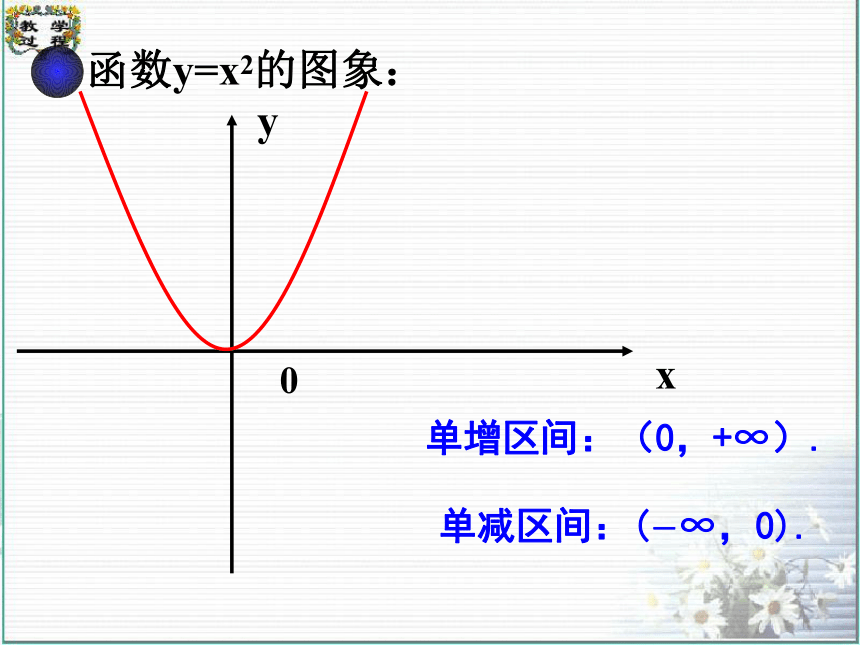
函数y=x2的图象:
y
x
0
单增区间:(0,+∞).
单减区间:(-∞,0).
注意:
如果在某个区间内恒有f′(x)=0,则f(x)为常数函数.
例1、已知导函数的下列信息:
试画出函数 图象的大致形状。
A
B
x
y
o
2
3
题组一、应用导数信息确定函数大致图象
例2:求函数f(x)=2x3-6x2+7的单调区间,
并画出草图.
解:函数的定义域为R,f′(x)=6x2-12x
令6x2-12x>0,解得x<0或x>2,
则f(x)的单增区间为(-∞,0)和
(2,+∞).
再令6x2-12x<0,解得0则f(x)的单减区间(0,2).
注:当x=0或2时, f′(x)=0,即函数在该点单
调性发生改变.
题组二、用导数判定函数的单调区间
巩固练习:求下列函数的单调区间
(3)
(2)
(1)y=sinx-x,x∈(0, π)
0
y
x
1
2
-1
-2
单增区间:(-∞,-1)和
(1,+∞).
单减区间:(-1,0)和
(0,1).
讨论函数 的单调性。
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
题组三、导数图像与原函数图象的关系
(全国卷理)
B
x
y
o
如果函数f(x)在某区间单增,则在该区间内 一定有 ?
结论:
如果函数f(x)在某区间单增,则在该区间内 有
如果在某区间内 ,则函数f(x)在该区间一定单增吗?
总结:根据导数确定函数的单调性
1.确定函数f(x)的定义域.
2.求出函数的导数.
3.解不等式f ′(x)>0,得函数单增区间;解不等式f′(x)<0,得函数单减区间.
作业
课本P26 1题(2)、(4);2题
思考题
(2)函数y=f(x)在定义域 内可导,其图象如图,记y=f(x)
的导函数为y=f′(x),则不等式f′(x)<0的解集为 .
【课后练习】(1)(2015·益阳高二检测)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
解:由已知得
因为函数在(0,1]上单调递增
过山车是一项富有刺激性的娱乐工具。那种风驰电掣、有惊无险的感觉令不少人着迷。
复习引入:
1、导数的定义
导数的几何意义
函数在一点处的导数,就是对应的函数图像在该点的切线的斜率。
复习引入:
2、函数的单调性的定义
对于给定区间上的函数f(x),如果对于属于这个区间的任意两个自变量的值x1,x2,
当x1
.
即x1-x2与f(x1)-f(x2)同号,即
当x1
那么f(x)在这个区间上是减函数
此时x1-x2与f(x1)-f(x2)异号,即
函数y=x2的图象:
y
x
0
单增区间:(0,+∞).
单减区间:(-∞,0).
注意:
如果在某个区间内恒有f′(x)=0,则f(x)为常数函数.
例1、已知导函数的下列信息:
试画出函数 图象的大致形状。
A
B
x
y
o
2
3
题组一、应用导数信息确定函数大致图象
例2:求函数f(x)=2x3-6x2+7的单调区间,
并画出草图.
解:函数的定义域为R,f′(x)=6x2-12x
令6x2-12x>0,解得x<0或x>2,
则f(x)的单增区间为(-∞,0)和
(2,+∞).
再令6x2-12x<0,解得0
注:当x=0或2时, f′(x)=0,即函数在该点单
调性发生改变.
题组二、用导数判定函数的单调区间
巩固练习:求下列函数的单调区间
(3)
(2)
(1)y=sinx-x,x∈(0, π)
0
y
x
1
2
-1
-2
单增区间:(-∞,-1)和
(1,+∞).
单减区间:(-1,0)和
(0,1).
讨论函数 的单调性。
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
题组三、导数图像与原函数图象的关系
(全国卷理)
B
x
y
o
如果函数f(x)在某区间单增,则在该区间内 一定有 ?
结论:
如果函数f(x)在某区间单增,则在该区间内 有
如果在某区间内 ,则函数f(x)在该区间一定单增吗?
总结:根据导数确定函数的单调性
1.确定函数f(x)的定义域.
2.求出函数的导数.
3.解不等式f ′(x)>0,得函数单增区间;解不等式f′(x)<0,得函数单减区间.
作业
课本P26 1题(2)、(4);2题
思考题
(2)函数y=f(x)在定义域 内可导,其图象如图,记y=f(x)
的导函数为y=f′(x),则不等式f′(x)<0的解集为 .
【课后练习】(1)(2015·益阳高二检测)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
解:由已知得
因为函数在(0,1]上单调递增
