人教版八年级上册11.2.1直角三角形 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.1直角三角形 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 339.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 19:41:28 | ||
图片预览



文档简介
(共18张PPT)
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.1 直角三角形
1. 了解直角三角形两个锐角的关系;(重点)
2. 掌握直角三角形的判定;(难点)
3. 会运用直角三角形的性质和判定进行相关计
算.(难点)
教学目标
新课引入
问题:已知△ABC的三个内角有以下关系:
∠B=∠A-40°,∠C=∠A-50°
你认为△ABC是什么三角形?
要记住,有一个角是90°的三角形就是直角三角形!
Rt△ABC
探究新知1
问题1:在刚刚的Rt△ABC中,∠A=90°,那么∠B和∠C呢?
问题2:在任何一个Rt△ABC中,若∠A=90°,∠B和∠C一定是什么角?他们之间又有什么关系呢?
想一想
探究新知1
问题3:是不是所有直角三角形都满足这样的关系呢?
1.直角三角形有一个直角和两个锐角。
2.直角三角形的两个锐角和为90°,即互余。
数学语言
探究新知1
A
B
C
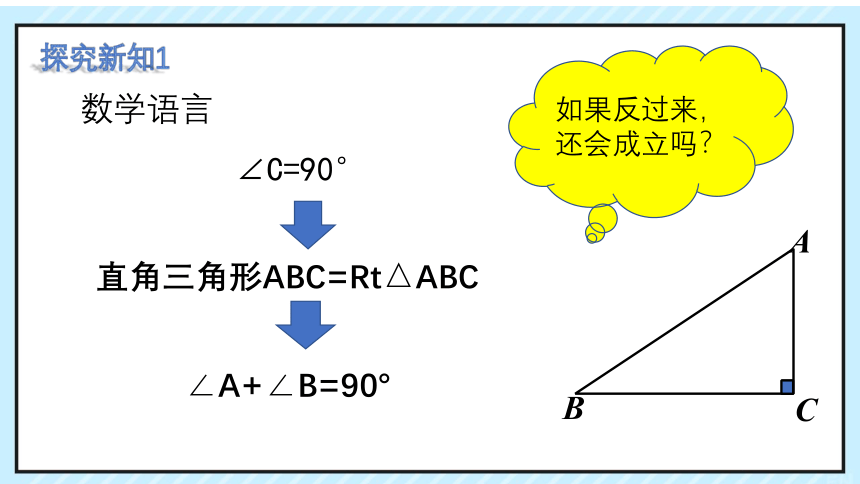
直角三角形ABC=Rt△ABC
∠C=90°
∠A+∠B=90°
如果反过来,还会成立吗?
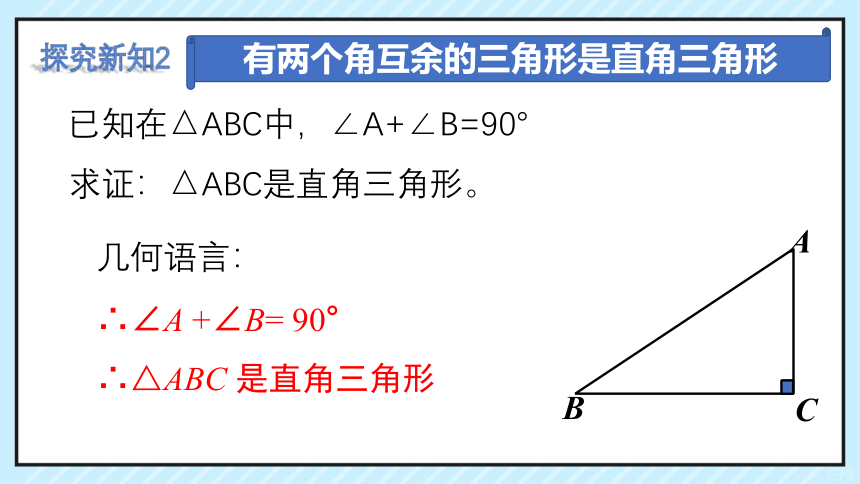
已知在△ABC中,∠A+∠B=90°
求证:△ABC是直角三角形。
探究新知2
A
B
C
有两个角互余的三角形是直角三角形
几何语言:
∴∠A +∠B= 90°
∴△ABC 是直角三角形
巩固新知1
1.(1)请找出一下子图形中,∠1 ,∠2 ,∠3 ,∠4的关系。
由三角形的内角和定理易得∠1 +∠2 =∠3 +∠4.
巩固新知1
(2)以下图形,∠A ,∠B,∠C ,∠D的关系是?
由三角形的内角和定理易得∠A +∠B =∠C +∠D.
巩固新知1
(3)∠A ,∠D关系是?
(4)∠A ,∠C关系是?
(3)∠A =∠D
(4)∠A =∠C
巩固新知1
(5)图中∠CAE,∠DBE的关系是什么?
A
B
C
D
E
∠CAE = ∠DBE
巩固新知1
(6)如图,△ABC 中,CD⊥AB 于 D,BE⊥AC于 E,CD,BE 相交于点 F,∠A 与∠BFC 又有什么关系?为什么?
巩固新知2
(2)如图,CE⊥AD,垂足为 E,
∠A = ∠C,△ABD是直角三角形
吗?为什么?
A
C
B
D
E
(
(
1
2
2.(1)如图,∠C = 90°,∠1 = ∠2,
则△ADE是 三角形。
总结归纳
直角三角形的两个锐角互余
有一个角是90°的三角形是直角三角形
有两个角互余的三角形是直角三角形
巩固练习
1. 在一个直角三角形中,有一个锐角等于 40°,则另一个锐角的度数是( )
A.40° B.50°
C.60° D.70°
B
巩固练习
2. 以下△ABC 中,不是直角三角形的是( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = 2∠B = 3∠C
D
巩固练习
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,CD⊥AB,则与∠1 互余的角有( )
A.∠B B.∠A
C.∠BCD 和 ∠A
D.∠BCD
C
巩固练习
4. 如图,在 Rt△ABC 中,∠ACB = 90°,D 是 AB 上一点,且∠ACD =∠B.求证:△ACD 是直角三角形.
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.1 直角三角形
1. 了解直角三角形两个锐角的关系;(重点)
2. 掌握直角三角形的判定;(难点)
3. 会运用直角三角形的性质和判定进行相关计
算.(难点)
教学目标
新课引入
问题:已知△ABC的三个内角有以下关系:
∠B=∠A-40°,∠C=∠A-50°
你认为△ABC是什么三角形?
要记住,有一个角是90°的三角形就是直角三角形!
Rt△ABC
探究新知1
问题1:在刚刚的Rt△ABC中,∠A=90°,那么∠B和∠C呢?
问题2:在任何一个Rt△ABC中,若∠A=90°,∠B和∠C一定是什么角?他们之间又有什么关系呢?
想一想
探究新知1
问题3:是不是所有直角三角形都满足这样的关系呢?
1.直角三角形有一个直角和两个锐角。
2.直角三角形的两个锐角和为90°,即互余。
数学语言
探究新知1
A
B
C
直角三角形ABC=Rt△ABC
∠C=90°
∠A+∠B=90°
如果反过来,还会成立吗?
已知在△ABC中,∠A+∠B=90°
求证:△ABC是直角三角形。
探究新知2
A
B
C
有两个角互余的三角形是直角三角形
几何语言:
∴∠A +∠B= 90°
∴△ABC 是直角三角形
巩固新知1
1.(1)请找出一下子图形中,∠1 ,∠2 ,∠3 ,∠4的关系。
由三角形的内角和定理易得∠1 +∠2 =∠3 +∠4.
巩固新知1
(2)以下图形,∠A ,∠B,∠C ,∠D的关系是?
由三角形的内角和定理易得∠A +∠B =∠C +∠D.
巩固新知1
(3)∠A ,∠D关系是?
(4)∠A ,∠C关系是?
(3)∠A =∠D
(4)∠A =∠C
巩固新知1
(5)图中∠CAE,∠DBE的关系是什么?
A
B
C
D
E
∠CAE = ∠DBE
巩固新知1
(6)如图,△ABC 中,CD⊥AB 于 D,BE⊥AC于 E,CD,BE 相交于点 F,∠A 与∠BFC 又有什么关系?为什么?
巩固新知2
(2)如图,CE⊥AD,垂足为 E,
∠A = ∠C,△ABD是直角三角形
吗?为什么?
A
C
B
D
E
(
(
1
2
2.(1)如图,∠C = 90°,∠1 = ∠2,
则△ADE是 三角形。
总结归纳
直角三角形的两个锐角互余
有一个角是90°的三角形是直角三角形
有两个角互余的三角形是直角三角形
巩固练习
1. 在一个直角三角形中,有一个锐角等于 40°,则另一个锐角的度数是( )
A.40° B.50°
C.60° D.70°
B
巩固练习
2. 以下△ABC 中,不是直角三角形的是( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = 2∠B = 3∠C
D
巩固练习
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,CD⊥AB,则与∠1 互余的角有( )
A.∠B B.∠A
C.∠BCD 和 ∠A
D.∠BCD
C
巩固练习
4. 如图,在 Rt△ABC 中,∠ACB = 90°,D 是 AB 上一点,且∠ACD =∠B.求证:△ACD 是直角三角形.
