初中数学苏科版(新版)七年级上册5.1丰富的图形世界 同步教学练习 (1)(word版含答案)
文档属性
| 名称 | 初中数学苏科版(新版)七年级上册5.1丰富的图形世界 同步教学练习 (1)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 15:48:55 | ||
图片预览

文档简介
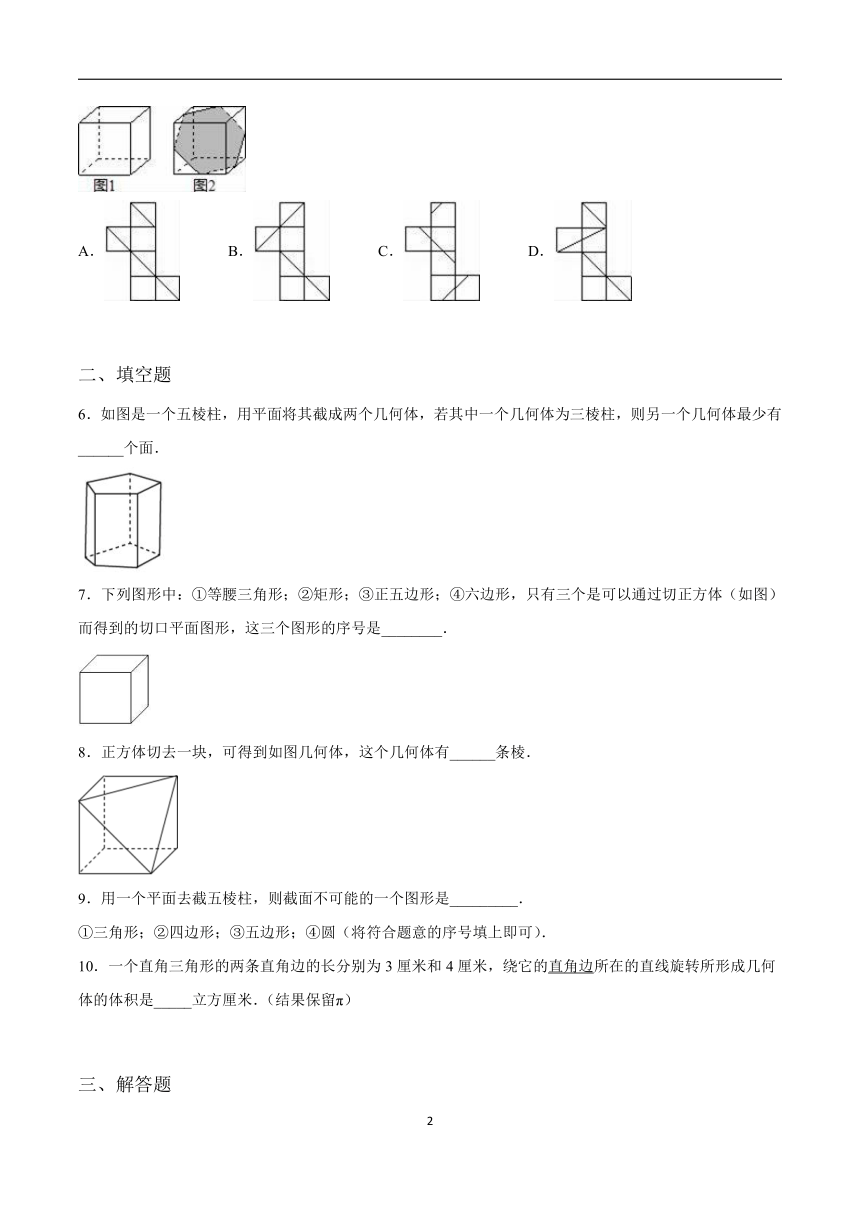
七年级上册5.1丰富的图形世界同步教学练习课堂练习
一、单选题
1.用一个平面截六棱柱,截面的形状不可能是( )
A.等腰三角形 B.梯形 C.五边形 D.九边形
2.如图,一个三棱柱共有侧棱( )
A.3条 B.5条 C.6条 D.9条
3.下列图形中,绕铅垂线旋转一周可得到如图所示几何体的是( )
A. B. C. D.
4.给出下列各说法:
①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( )
A.①② B.②③ C.②④ D.③④
5.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是( )
A. B. C. D.
二、填空题
6.如图是一个五棱柱,用平面将其截成两个几何体,若其中一个几何体为三棱柱,则另一个几何体最少有______个面.
7.下列图形中:①等腰三角形;②矩形;③正五边形;④六边形,只有三个是可以通过切正方体(如图)而得到的切口平面图形,这三个图形的序号是________.
8.正方体切去一块,可得到如图几何体,这个几何体有______条棱.
9.用一个平面去截五棱柱,则截面不可能的一个图形是_________.
①三角形;②四边形;③五边形;④圆(将符合题意的序号填上即可).
10.一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的体积是_____立方厘米.(结果保留π)
三、解答题
11.如图是一张长方形纸片,长为,长为.
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕边所在直线旋转一周,则形成的几何体的体积是____(结果保留);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留).
12.如图,把一个棱长8厘米的正方体的六个面都涂上红色,再将它的棱四等分,然后从等分点把正方体锯开.
(1)能得到多少个棱长为2厘米的小正方体?
(2)三个面有红色的小正方体有多少个?
(3)两个面有红色的小正方体有多少个?
(4)一个面有红色的小正方体有多少个?
(5)有没有各面都没有红色的小正方体?如果有,那么有多少个?
13.欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.
14.如图,第二行的图形绕虚线旋转一周,便能得到第一行的某个几何体.用线连一连.
15.一个六棱柱模型如图所示,它的底面边长都是5,侧棱长是4.观察这个模型,回答下列问题.
(1)这个六棱柱一共有多少个面?它们分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱一共有多少条棱?它们的长度分别是多少?
参考答案与试题解析
1.D
2.A
3.A
4.C
5.C
6.6
7.①②④
8.12
9.④
10.或
11.(1)圆柱;(2);(3)或.
12.(1)64个
(2)8个
(3)24个
(4)24个
(5)有,8个
13.(1)表格详见解析;(2)
14.见解析.
15.(1)8,长方形,正六边形,6个侧面,2个底面;
(2)18, 侧棱长都是4,底边长都是5.
2
一、单选题
1.用一个平面截六棱柱,截面的形状不可能是( )
A.等腰三角形 B.梯形 C.五边形 D.九边形
2.如图,一个三棱柱共有侧棱( )
A.3条 B.5条 C.6条 D.9条
3.下列图形中,绕铅垂线旋转一周可得到如图所示几何体的是( )
A. B. C. D.
4.给出下列各说法:
①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( )
A.①② B.②③ C.②④ D.③④
5.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是( )
A. B. C. D.
二、填空题
6.如图是一个五棱柱,用平面将其截成两个几何体,若其中一个几何体为三棱柱,则另一个几何体最少有______个面.
7.下列图形中:①等腰三角形;②矩形;③正五边形;④六边形,只有三个是可以通过切正方体(如图)而得到的切口平面图形,这三个图形的序号是________.
8.正方体切去一块,可得到如图几何体,这个几何体有______条棱.
9.用一个平面去截五棱柱,则截面不可能的一个图形是_________.
①三角形;②四边形;③五边形;④圆(将符合题意的序号填上即可).
10.一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的体积是_____立方厘米.(结果保留π)
三、解答题
11.如图是一张长方形纸片,长为,长为.
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕边所在直线旋转一周,则形成的几何体的体积是____(结果保留);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留).
12.如图,把一个棱长8厘米的正方体的六个面都涂上红色,再将它的棱四等分,然后从等分点把正方体锯开.
(1)能得到多少个棱长为2厘米的小正方体?
(2)三个面有红色的小正方体有多少个?
(3)两个面有红色的小正方体有多少个?
(4)一个面有红色的小正方体有多少个?
(5)有没有各面都没有红色的小正方体?如果有,那么有多少个?
13.欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数V 4 6 8
棱数E 6 12
面数F 4 5 8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.
14.如图,第二行的图形绕虚线旋转一周,便能得到第一行的某个几何体.用线连一连.
15.一个六棱柱模型如图所示,它的底面边长都是5,侧棱长是4.观察这个模型,回答下列问题.
(1)这个六棱柱一共有多少个面?它们分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱一共有多少条棱?它们的长度分别是多少?
参考答案与试题解析
1.D
2.A
3.A
4.C
5.C
6.6
7.①②④
8.12
9.④
10.或
11.(1)圆柱;(2);(3)或.
12.(1)64个
(2)8个
(3)24个
(4)24个
(5)有,8个
13.(1)表格详见解析;(2)
14.见解析.
15.(1)8,长方形,正六边形,6个侧面,2个底面;
(2)18, 侧棱长都是4,底边长都是5.
2
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
