初中数学苏科版(新版)七年级上册5.1丰富的图形世界 同步教学练习(word版含答案)
文档属性
| 名称 | 初中数学苏科版(新版)七年级上册5.1丰富的图形世界 同步教学练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览

文档简介
七年级上册5.1丰富的图形世界同步教学练习优质练习
一、单选题
1.如图,该几何体的截面形状是( )
A.三角形 B.长方形 C.圆形 D.五边形
2.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
3.给出下列结论:①圆柱由三个面围成,这三个面都是平的;②圆锥由两个面围成,这两个面中,一个面是平的,一个面是曲的;③球仅由一个面围成,这个面是曲的;④长方体由六个面围成,这六个面都是平的其中正确的有( ).
A.①②③ B.①③④ C.②③④ D.①②④
4.下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.③⑥ D.④⑤
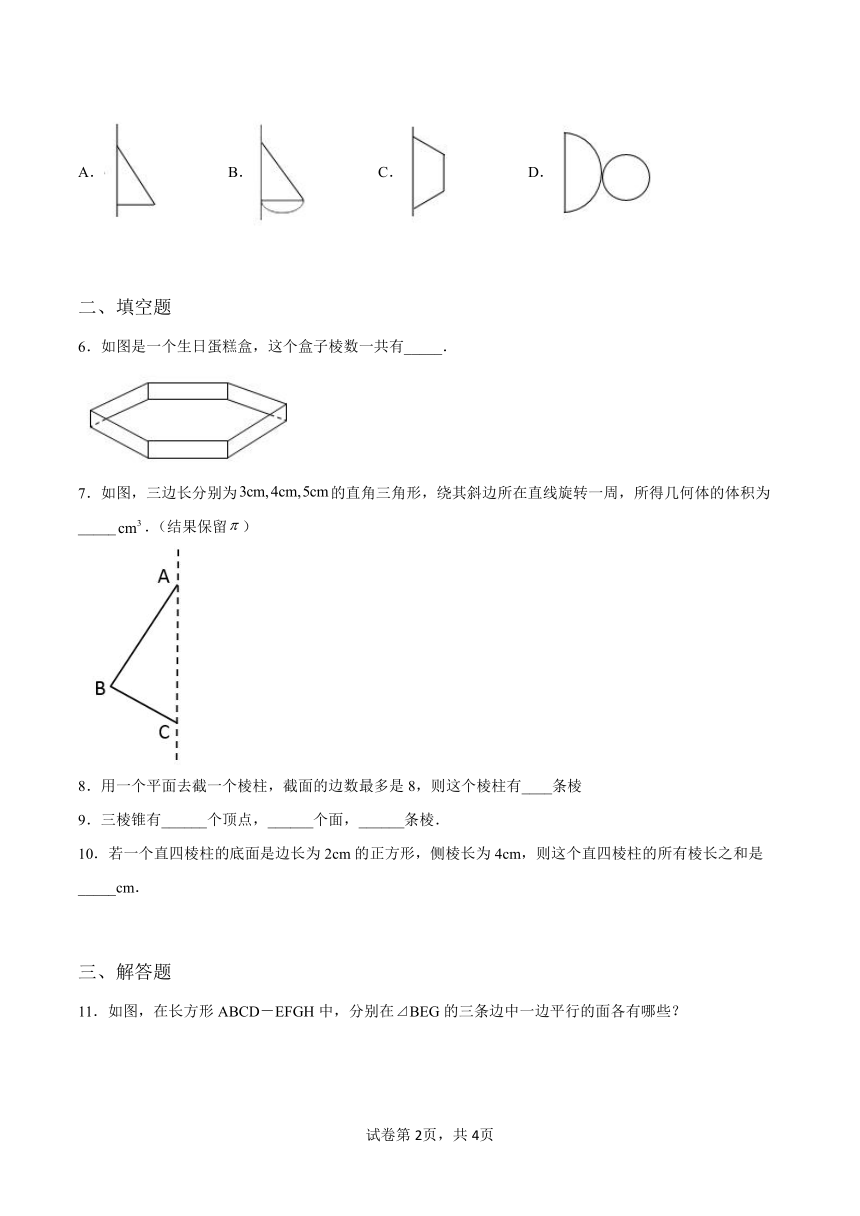
5.下图中的几何体(圆锥)是由下列( )平面图形绕轴旋转一周得到的.
A. B. C. D.
二、填空题
6.如图是一个生日蛋糕盒,这个盒子棱数一共有_____.
7.如图,三边长分别为的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为_____.(结果保留)
8.用一个平面去截一个棱柱,截面的边数最多是8,则这个棱柱有____条棱
9.三棱锥有______个顶点,______个面,______条棱.
10.若一个直四棱柱的底面是边长为2cm的正方形,侧棱长为4cm,则这个直四棱柱的所有棱长之和是_____cm.
三、解答题
11.如图,在长方形ABCD-EFGH中,分别在⊿BEG的三条边中一边平行的面各有哪些?
12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4
长方体 8 12
正八面体 8 12
正十二面体 20 12 30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是___________;
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是___________;
(4)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.该多面体外表面三角形的个数为x个,八边形的个数为y个,求的值.
13.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
14.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
15.数一数,在长方体ABCD-EFGH中,有多少对平行的棱?有多少对相交的棱?有多少对异面的棱?
参考答案与试题解析
1.B
2.B
3.C
4.A
5.A
6.18
7.
8.18
9. 4 4 6
10.32
11.与EG平行的面是面ABCD;与BG平行的面是面ADHE;与BE平行的面是面CDHG.
12.(1)4,6,6,6;(2);(3)20;(4)14
13.答案见解析
14.(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
15.有18对平行的棱,24对相交的棱,24对异面的棱
试卷第4页,共4页
试卷第4页,共4页
一、单选题
1.如图,该几何体的截面形状是( )
A.三角形 B.长方形 C.圆形 D.五边形
2.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
3.给出下列结论:①圆柱由三个面围成,这三个面都是平的;②圆锥由两个面围成,这两个面中,一个面是平的,一个面是曲的;③球仅由一个面围成,这个面是曲的;④长方体由六个面围成,这六个面都是平的其中正确的有( ).
A.①②③ B.①③④ C.②③④ D.①②④
4.下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.③⑥ D.④⑤
5.下图中的几何体(圆锥)是由下列( )平面图形绕轴旋转一周得到的.
A. B. C. D.
二、填空题
6.如图是一个生日蛋糕盒,这个盒子棱数一共有_____.
7.如图,三边长分别为的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为_____.(结果保留)
8.用一个平面去截一个棱柱,截面的边数最多是8,则这个棱柱有____条棱
9.三棱锥有______个顶点,______个面,______条棱.
10.若一个直四棱柱的底面是边长为2cm的正方形,侧棱长为4cm,则这个直四棱柱的所有棱长之和是_____cm.
三、解答题
11.如图,在长方形ABCD-EFGH中,分别在⊿BEG的三条边中一边平行的面各有哪些?
12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4
长方体 8 12
正八面体 8 12
正十二面体 20 12 30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是___________;
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是___________;
(4)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.该多面体外表面三角形的个数为x个,八边形的个数为y个,求的值.
13.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
14.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
15.数一数,在长方体ABCD-EFGH中,有多少对平行的棱?有多少对相交的棱?有多少对异面的棱?
参考答案与试题解析
1.B
2.B
3.C
4.A
5.A
6.18
7.
8.18
9. 4 4 6
10.32
11.与EG平行的面是面ABCD;与BG平行的面是面ADHE;与BE平行的面是面CDHG.
12.(1)4,6,6,6;(2);(3)20;(4)14
13.答案见解析
14.(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
15.有18对平行的棱,24对相交的棱,24对异面的棱
试卷第4页,共4页
试卷第4页,共4页
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
