初中数学人教版七年级下册5.2平行线及其判定 同步课时练习(word版含答案)
文档属性
| 名称 | 初中数学人教版七年级下册5.2平行线及其判定 同步课时练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 16:25:40 | ||
图片预览




文档简介
初中数学人教版七年级下册5.2平行线及其判定同步课时练习
一.选择题
1. 如图,要得到a∥b,则需要条件( )
A.∠1+∠2=180° B.∠1+∠3=180° C.∠2=∠4 D.∠2=∠3
2. 如图所示,AD⊥BC,则∠ADE与∠B的关系满足什么关系时,才能保证DE∥AB ( )
A.相等 B.互补 C.互余 D.不能确定
3. 如图,下列条件: ① : ② ; ③ ; ④ ,其中能判定 的有 ( )
A . 1 个 B . 2 个 C . 4 个 D . 3 个
4.
如图,点 在 的延长线上,下列条件中不能判定 的是( )
A . B .
C . D .
5. 如图,下列条件不能判断 的是( )
A . B . C . D .
6. 如图, ,要使 ,则 的大小是( )
A . B . C . D .
二.填空题
7. 如图,AB//CD,CE平分∠ACD,若∠1=250,那么∠2的度数是 .
8. 对于同一平面内的三条直线..,给出下列五个论断:(1)∥;(2)∥;(3)⊥;(4)∥;(5)⊥。以其中两个论断为条件,一个论断为结论,组成一个你认为正确的题 目 .(写出一组即可)
9. 如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知)。所以AD∥BC( )。
10. 如图,直线a.b都与c相交,给出条件:
①∠1=∠2,②∠3=∠6,③∠4+∠7=180°④∠5+∠8=180°,其中能判断a∥b的条件是 (只填序号)。
11. 如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
∵∠5=∠CDA(已知)
∴ // ( )
∵∠5=∠ABC(已知)
∴ // ( )
∵∠2=∠3(已知)
∴ // ( )
∵∠BAD+∠CDA=180°(已知)
∴ // ( )
∵∠5=∠CDA(已知),又∵∠5与∠BCD互补( )
∠CDA与 互补(邻补角定义)
∴∠BCD=∠6( )
∴ // ( )
三.解答题
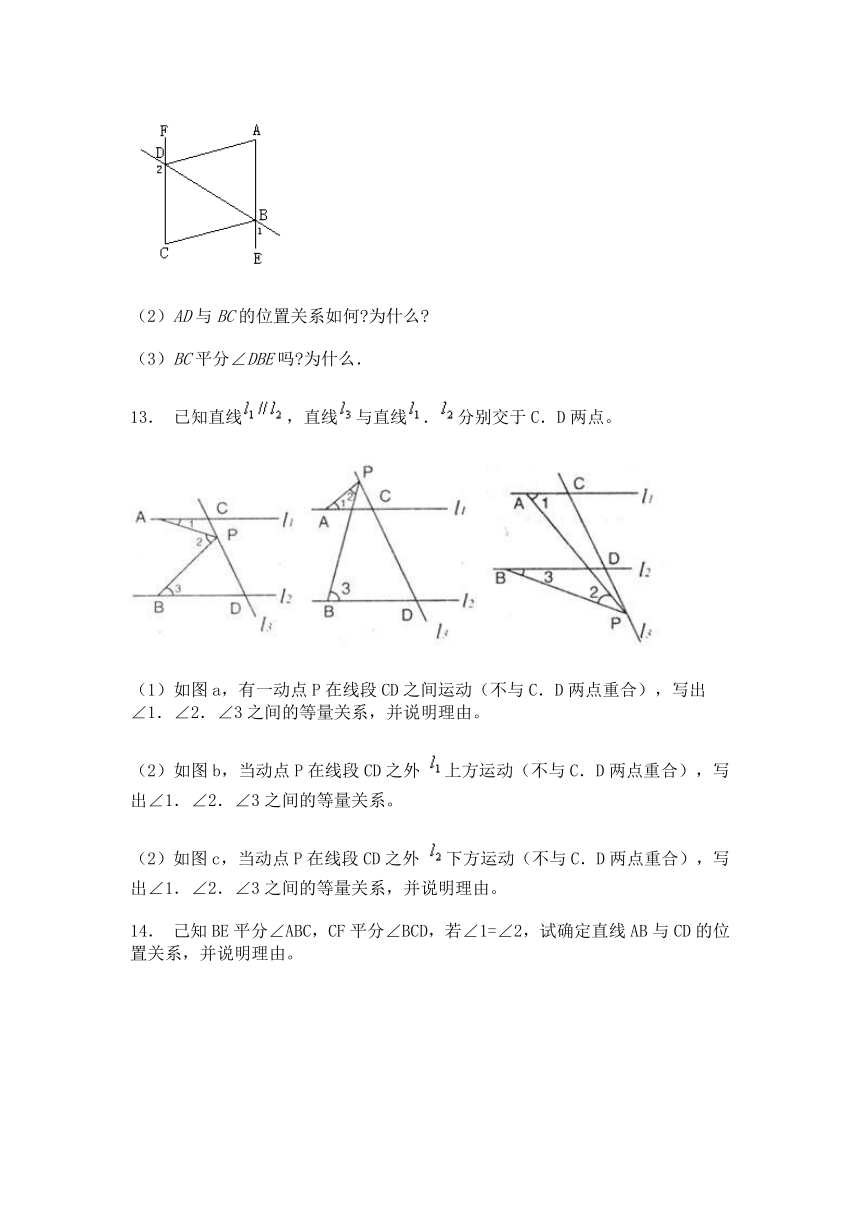
12. 如图∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)BC平分∠DBE吗 为什么.
13. 已知直线,直线与直线.分别交于C.D两点。
(1)如图a,有一动点P在线段CD之间运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系,并说明理由。
(2)如图b,当动点P在线段CD之外 上方运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系。
(2)如图c,当动点P在线段CD之外 下方运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系,并说明理由。
14. 己知BE平分∠ABC,CF平分∠BCD,若∠1=∠2,试确定直线AB与CD的位置关系,并说明理由。
参考答案与试题解析
1. A
2. C
二.填空题
3;
经过直线外一点,有且只有一条 直线与这条直线平行
∠EDA=∠B ∠DAC=∠C ∠DAB+∠B=180
如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
∵∠5=∠CDA(已知)
∴ AD // BE ( 内错角相等,两直线平行 )
∵∠5=∠ABC(已知)
∴ AB //DC ( 同位角相等,两直线平行 )
∵∠2=∠3(已知)
∴ AB // CD ( 内错角相等,两直线平行 )
∵∠BAD+∠CDA=180°(已知)
∴ AB // CD (同旁内角互补,两直线平行 )
∵∠5=∠CDA(已知),
又∵∠5与∠BCD互补( 邻补角定义 )
∠CDA与 ∠6 互补(邻补角定义)
∴∠BCD=∠6( 同角的补角相等 )
∴ AD // BE ( )
①②③④
答案不唯一 .
∠BAC=∠ACD(答案不唯一)
50
∠1=∠2
9
内错角相等,两直线平行;
3. B
4. D
5. C
6. D
7. (1)平行
因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)
所以∠1=∠CDB
所以AE∥FC( 同位角相等两直线平行)
(2)平行,
因为AE∥CF,
所以∠C=∠CBE(两直线平行, 内错角相等)
又∠A=∠C 所以∠A=∠CBE
所以AF∥BC(两直线平行,内错角相等)
(3) 平分
因为DA平分∠BDF,
所以∠FDA=∠ADB
因为AE∥CF,AD∥BC
所以∠FDA=∠A=∠CBE,∠ADB=∠CBD
所以∠EBC=∠CBD
8. 解:(1)∠1.∠2.∠3之间的等量关系为∠1+∠3=∠2。
过P做直线PE//
所以∠1=∠APE
因为所以PE//
所以∠3=∠BPE
所以∠1+∠3=∠APE+∠BPE=∠2
(2)∠1.∠2.∠3之间的等量关系为∠1+∠2=∠3。
(3)∠1.∠2.∠3之间的等量关系为∠3+∠2=∠1。
9. 解:AB//CD
∵BE平分∠ABC CF平分∠BCD
∵∠ABC=2∠1 ∠BCD=2∠2
∴∠1=∠2 ∴∠ABC=∠BCD
∴AB∥CD
一.选择题
1. 如图,要得到a∥b,则需要条件( )
A.∠1+∠2=180° B.∠1+∠3=180° C.∠2=∠4 D.∠2=∠3
2. 如图所示,AD⊥BC,则∠ADE与∠B的关系满足什么关系时,才能保证DE∥AB ( )
A.相等 B.互补 C.互余 D.不能确定
3. 如图,下列条件: ① : ② ; ③ ; ④ ,其中能判定 的有 ( )
A . 1 个 B . 2 个 C . 4 个 D . 3 个
4.
如图,点 在 的延长线上,下列条件中不能判定 的是( )
A . B .
C . D .
5. 如图,下列条件不能判断 的是( )
A . B . C . D .
6. 如图, ,要使 ,则 的大小是( )
A . B . C . D .
二.填空题
7. 如图,AB//CD,CE平分∠ACD,若∠1=250,那么∠2的度数是 .
8. 对于同一平面内的三条直线..,给出下列五个论断:(1)∥;(2)∥;(3)⊥;(4)∥;(5)⊥。以其中两个论断为条件,一个论断为结论,组成一个你认为正确的题 目 .(写出一组即可)
9. 如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知)。所以AD∥BC( )。
10. 如图,直线a.b都与c相交,给出条件:
①∠1=∠2,②∠3=∠6,③∠4+∠7=180°④∠5+∠8=180°,其中能判断a∥b的条件是 (只填序号)。
11. 如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
∵∠5=∠CDA(已知)
∴ // ( )
∵∠5=∠ABC(已知)
∴ // ( )
∵∠2=∠3(已知)
∴ // ( )
∵∠BAD+∠CDA=180°(已知)
∴ // ( )
∵∠5=∠CDA(已知),又∵∠5与∠BCD互补( )
∠CDA与 互补(邻补角定义)
∴∠BCD=∠6( )
∴ // ( )
三.解答题
12. 如图∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)BC平分∠DBE吗 为什么.
13. 已知直线,直线与直线.分别交于C.D两点。
(1)如图a,有一动点P在线段CD之间运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系,并说明理由。
(2)如图b,当动点P在线段CD之外 上方运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系。
(2)如图c,当动点P在线段CD之外 下方运动(不与C.D两点重合),写出∠1.∠2.∠3之间的等量关系,并说明理由。
14. 己知BE平分∠ABC,CF平分∠BCD,若∠1=∠2,试确定直线AB与CD的位置关系,并说明理由。
参考答案与试题解析
1. A
2. C
二.填空题
3;
经过直线外一点,有且只有一条 直线与这条直线平行
∠EDA=∠B ∠DAC=∠C ∠DAB+∠B=180
如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
∵∠5=∠CDA(已知)
∴ AD // BE ( 内错角相等,两直线平行 )
∵∠5=∠ABC(已知)
∴ AB //DC ( 同位角相等,两直线平行 )
∵∠2=∠3(已知)
∴ AB // CD ( 内错角相等,两直线平行 )
∵∠BAD+∠CDA=180°(已知)
∴ AB // CD (同旁内角互补,两直线平行 )
∵∠5=∠CDA(已知),
又∵∠5与∠BCD互补( 邻补角定义 )
∠CDA与 ∠6 互补(邻补角定义)
∴∠BCD=∠6( 同角的补角相等 )
∴ AD // BE ( )
①②③④
答案不唯一 .
∠BAC=∠ACD(答案不唯一)
50
∠1=∠2
9
内错角相等,两直线平行;
3. B
4. D
5. C
6. D
7. (1)平行
因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)
所以∠1=∠CDB
所以AE∥FC( 同位角相等两直线平行)
(2)平行,
因为AE∥CF,
所以∠C=∠CBE(两直线平行, 内错角相等)
又∠A=∠C 所以∠A=∠CBE
所以AF∥BC(两直线平行,内错角相等)
(3) 平分
因为DA平分∠BDF,
所以∠FDA=∠ADB
因为AE∥CF,AD∥BC
所以∠FDA=∠A=∠CBE,∠ADB=∠CBD
所以∠EBC=∠CBD
8. 解:(1)∠1.∠2.∠3之间的等量关系为∠1+∠3=∠2。
过P做直线PE//
所以∠1=∠APE
因为所以PE//
所以∠3=∠BPE
所以∠1+∠3=∠APE+∠BPE=∠2
(2)∠1.∠2.∠3之间的等量关系为∠1+∠2=∠3。
(3)∠1.∠2.∠3之间的等量关系为∠3+∠2=∠1。
9. 解:AB//CD
∵BE平分∠ABC CF平分∠BCD
∵∠ABC=2∠1 ∠BCD=2∠2
∴∠1=∠2 ∴∠ABC=∠BCD
∴AB∥CD
