24.2.2 直线和圆的位置关系(切线的性质定理) 同步跟踪测试(含答案)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(切线的性质定理) 同步跟踪测试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 16:05:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系(切线的性质定理)
一、单选题
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 ( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.20° B.25° C.40° D.50°
2.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
( http: / / www.21cnjy.com / )
A.55° B.70° C.110° D.125°
3.如图,AB为的切线,切点为A,连接AO、BO,,BO与交于点C,延长BO与交于点D,连接AD,若,则的度数为( )www.21-cn-jy.com
A. B. C. D.
4.如图,.分别与相切于.两点,点为上一点,连接.,若,则的度数为( ).【来源:21·世纪·教育·网】
A.; B.; C.; D..
5.如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A.70° B.50° C.45° D.20°
6.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.15° B.30° C.35° D.45°
7.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连结OD,若∠BAC=55°,则∠COD的大小为( )21教育名师原创作品
( http: / / www.21cnjy.com / )
A.70° B.60° C.55° D.35°
9.如图,为的直径,为上一点,和过点的切线互相垂直,垂足为.若,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,等边三角形的边长为8,以上一点为圆心的圆分别与边,相切,则的半径为( ) ( http: / / www.21cnjy.com / )21教育网
A. B.3 C.4 D.
二、填空题
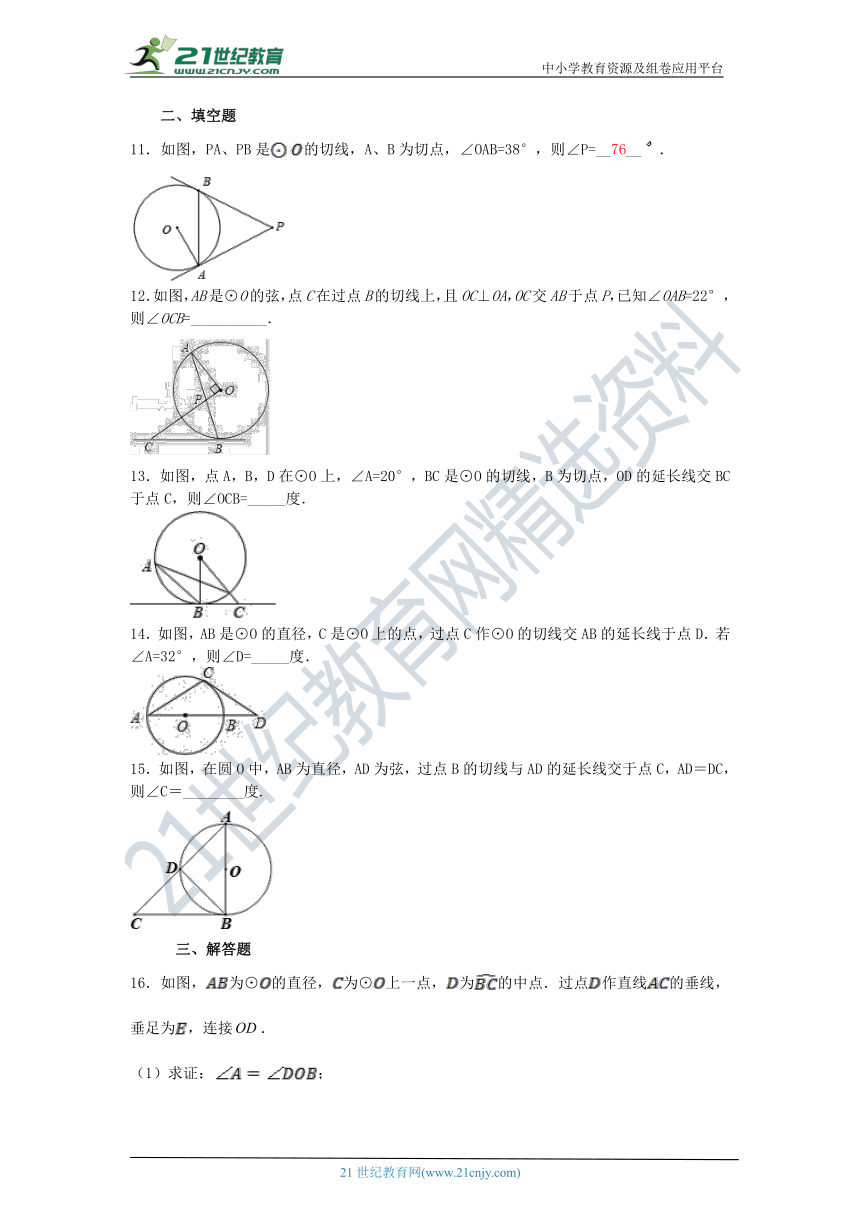
11.如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__76__.
( http: / / www.21cnjy.com / )
12.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
( http: / / www.21cnjy.com / )
13.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=_____度.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
14.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=_____度.
( http: / / www.21cnjy.com / )
15.如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C=________度.
( http: / / www.21cnjy.com / )
三、解答题
16.如图,为⊙的直径,为⊙上一点,为的中点.过点作直线的垂线,垂足为,连接.
(1)求证:;
(2)与⊙有怎样的位置关系?请说明理由.
( http: / / www.21cnjy.com / )
17.如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=(90°﹣∠P)成立.请你写出推理过程.
( http: / / www.21cnjy.com / )
24.2.2 直线和圆的位置关系(切线的性质定理)参考答案
一、单选题
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 ( B )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A.20° B.25° C.40° D.50°
2.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( B )
( http: / / www.21cnjy.com / )
A.55° B.70° C.110° D.125°
3.如图,AB为的切线,切点为A,连接AO、BO,,BO与交于点C,延长BO与交于点D,连接AD,若,则的度数为( D )www-2-1-cnjy-com
A. B. C. D.
4.如图,.分别与相切于.两点,点为上一点,连接.,若,则的度数为( D ).【来源:21cnj*y.co*m】
A.; B.; C.; D..
5.如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( B )
( http: / / www.21cnjy.com / )
A.70° B.50° C.45° D.20°
6.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( C )
( http: / / www.21cnjy.com / )
A.15° B.30° C.35° D.45°
7.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( A )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连结OD,若∠BAC=55°,则∠COD的大小为( A )
( http: / / www.21cnjy.com / )
A.70° B.60° C.55° D.35°
9.如图,为的直径,为上一点,和过点的切线互相垂直,垂足为.若,则的度数为( B )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,等边三角形的边长为8,以上一点为圆心的圆分别与边,相切,则的半径为( A ) ( http: / / www.21cnjy.com / )21cnjy.com
A. B.3 C.4 D.
二、填空题
11.如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__76__.
( http: / / www.21cnjy.com / )
12.如图,AB是⊙O的弦,点C ( http: / / www.21cnjy.com )在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=______44°____.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
13.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=___50__度.21*cnjy*com
( http: / / www.21cnjy.com / )
14.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=___26__度.21*cnjy*com
( http: / / www.21cnjy.com / )
15.如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C=____45____度.
( http: / / www.21cnjy.com / )
三、解答题
16.如图,为⊙的直径,为⊙上一点,为的中点.过点作直线的垂线,垂足为,连接.
(1)求证:;
(2)与⊙有怎样的位置关系?请说明理由.
( http: / / www.21cnjy.com / )
解:(1)连接,为的中点,∴,,
,;
(2)与⊙相切,理由如下: ,,∴∠ODE+∠E=180°,
,∴∠E=90°,∴∠ODE=90°,,
又∵OD是半径,∴DE与⊙相切. ( http: / / www.21cnjy.com / )
17.如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=(90°﹣∠P)成立.请你写出推理过程.
( http: / / www.21cnjy.com / )
解:(1)连接OC, ( http: / / www.21cnjy.com / )
∵AB是直径,∴∠ACB=90°,
又∵∠A=30°,∴∠ABC=90°-30°=60°,
∵OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠COB=60°,
∵PC是⊙O的切线,OC是半径,∴∠OCP=90°,∴∠P=90°-∠BOC=30°,
∴PO=2OC,∴PB=OB,∵AB=2OB,∴AP=AB+PB=3PB;
(2)如图,连接OC, ( http: / / www.21cnjy.com / )
∵AB是直径,∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵PC是⊙O的切线,OC是半径,∴∠OCP=90°,即∠BCP+∠BCO=90°,∴∠BCP=∠ACO,
∵OA=OC,∴∠A=∠ACO,∴∠BCP=∠A,
∵∠A+∠P+∠ACB+∠BCP=180°,且∠ACB=90°,∴2∠BCP=180°﹣∠P,
∴∠BCP= (90°﹣∠P).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.2.2 直线和圆的位置关系(切线的性质定理)
一、单选题
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 ( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.20° B.25° C.40° D.50°
2.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
( http: / / www.21cnjy.com / )
A.55° B.70° C.110° D.125°
3.如图,AB为的切线,切点为A,连接AO、BO,,BO与交于点C,延长BO与交于点D,连接AD,若,则的度数为( )www.21-cn-jy.com
A. B. C. D.
4.如图,.分别与相切于.两点,点为上一点,连接.,若,则的度数为( ).【来源:21·世纪·教育·网】
A.; B.; C.; D..
5.如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A.70° B.50° C.45° D.20°
6.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.15° B.30° C.35° D.45°
7.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连结OD,若∠BAC=55°,则∠COD的大小为( )21教育名师原创作品
( http: / / www.21cnjy.com / )
A.70° B.60° C.55° D.35°
9.如图,为的直径,为上一点,和过点的切线互相垂直,垂足为.若,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,等边三角形的边长为8,以上一点为圆心的圆分别与边,相切,则的半径为( ) ( http: / / www.21cnjy.com / )21教育网
A. B.3 C.4 D.
二、填空题
11.如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__76__.
( http: / / www.21cnjy.com / )
12.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
( http: / / www.21cnjy.com / )
13.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=_____度.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
14.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=_____度.
( http: / / www.21cnjy.com / )
15.如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C=________度.
( http: / / www.21cnjy.com / )
三、解答题
16.如图,为⊙的直径,为⊙上一点,为的中点.过点作直线的垂线,垂足为,连接.
(1)求证:;
(2)与⊙有怎样的位置关系?请说明理由.
( http: / / www.21cnjy.com / )
17.如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=(90°﹣∠P)成立.请你写出推理过程.
( http: / / www.21cnjy.com / )
24.2.2 直线和圆的位置关系(切线的性质定理)参考答案
一、单选题
1.如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为 ( B )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A.20° B.25° C.40° D.50°
2.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( B )
( http: / / www.21cnjy.com / )
A.55° B.70° C.110° D.125°
3.如图,AB为的切线,切点为A,连接AO、BO,,BO与交于点C,延长BO与交于点D,连接AD,若,则的度数为( D )www-2-1-cnjy-com
A. B. C. D.
4.如图,.分别与相切于.两点,点为上一点,连接.,若,则的度数为( D ).【来源:21cnj*y.co*m】
A.; B.; C.; D..
5.如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( B )
( http: / / www.21cnjy.com / )
A.70° B.50° C.45° D.20°
6.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( C )
( http: / / www.21cnjy.com / )
A.15° B.30° C.35° D.45°
7.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( A )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连结OD,若∠BAC=55°,则∠COD的大小为( A )
( http: / / www.21cnjy.com / )
A.70° B.60° C.55° D.35°
9.如图,为的直径,为上一点,和过点的切线互相垂直,垂足为.若,则的度数为( B )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,等边三角形的边长为8,以上一点为圆心的圆分别与边,相切,则的半径为( A ) ( http: / / www.21cnjy.com / )21cnjy.com
A. B.3 C.4 D.
二、填空题
11.如图,PA、PB是的切线,A、B为切点,∠OAB=38°,则∠P=__76__.
( http: / / www.21cnjy.com / )
12.如图,AB是⊙O的弦,点C ( http: / / www.21cnjy.com )在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=______44°____.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
13.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=___50__度.21*cnjy*com
( http: / / www.21cnjy.com / )
14.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D.若∠A=32°,则∠D=___26__度.21*cnjy*com
( http: / / www.21cnjy.com / )
15.如图,在圆O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C,AD=DC,则∠C=____45____度.
( http: / / www.21cnjy.com / )
三、解答题
16.如图,为⊙的直径,为⊙上一点,为的中点.过点作直线的垂线,垂足为,连接.
(1)求证:;
(2)与⊙有怎样的位置关系?请说明理由.
( http: / / www.21cnjy.com / )
解:(1)连接,为的中点,∴,,
,;
(2)与⊙相切,理由如下: ,,∴∠ODE+∠E=180°,
,∴∠E=90°,∴∠ODE=90°,,
又∵OD是半径,∴DE与⊙相切. ( http: / / www.21cnjy.com / )
17.如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
(1)若∠A=30°,求证:PA=3PB;
(2)小明发现,∠A在一定范围内变化时,始终有∠BCP=(90°﹣∠P)成立.请你写出推理过程.
( http: / / www.21cnjy.com / )
解:(1)连接OC, ( http: / / www.21cnjy.com / )
∵AB是直径,∴∠ACB=90°,
又∵∠A=30°,∴∠ABC=90°-30°=60°,
∵OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠COB=60°,
∵PC是⊙O的切线,OC是半径,∴∠OCP=90°,∴∠P=90°-∠BOC=30°,
∴PO=2OC,∴PB=OB,∵AB=2OB,∴AP=AB+PB=3PB;
(2)如图,连接OC, ( http: / / www.21cnjy.com / )
∵AB是直径,∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵PC是⊙O的切线,OC是半径,∴∠OCP=90°,即∠BCP+∠BCO=90°,∴∠BCP=∠ACO,
∵OA=OC,∴∠A=∠ACO,∴∠BCP=∠A,
∵∠A+∠P+∠ACB+∠BCP=180°,且∠ACB=90°,∴2∠BCP=180°﹣∠P,
∴∠BCP= (90°﹣∠P).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
