数学人教A版2019选择性必修第一册2.2.1直线的点斜式方程 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版2019选择性必修第一册2.2.1直线的点斜式方程 课件(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
2.2直线的方程
直线和圆的方程
2.2.1直线的点斜式方程
课程标准
在平面直角坐标系中,根据确定直线位置的几何要素(点+斜率),探索直线的点斜式方程,并掌握直线的点斜式方程。
复习回顾
问题1 如何求直线的斜率?
问题2 如何判断直线的平行与垂直?
通过直线斜率进行判断
l1//l2=.
l1l2=1.
新课导入
导
问题2 如何确定一条直线?
已知两点可以确定一条直线。
已知直线上的一点和直线的倾斜角(斜率)可以确定一条直线。
这样,在平面直角坐标系中,给定一个点和斜率k(或倾斜角),就能唯一确定一条直线.也就是说,这条直线上任意一点的坐标(x,y)与点的坐标和斜率k之间的关系是完全确定的。
那么,我们下面来探究点和斜率k(或倾斜角)之间的关系
一
二
三
教学目标
了解由斜率公式推导直线方程的点斜式的过程
掌握直线的点斜式方程和斜截式方程,并会用它们求直线的方程
会利用直线的点斜式和斜截式方程解决有关的问题
教学目标
难点
重点
新知探究
探究一:过点且斜率为k(或倾斜角为)的直线方程
新知讲解
如图,直线经过点,且斜率为.设是直线上不同于点的任意一点,因为直线l的斜率为k,由斜率公式得
(x,y)
即
追问:点的坐标满足关系式吗?
新知讲解
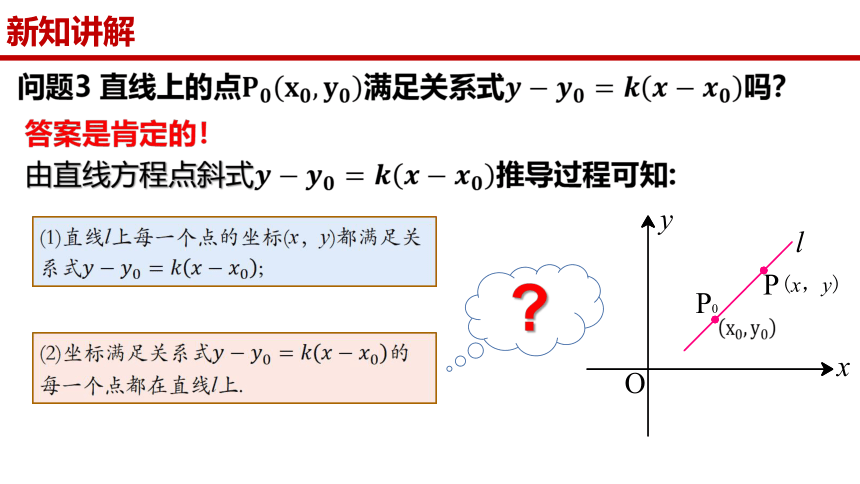
问题3 直线上的点满足关系式吗?
(x,y)
答案是肯定的!
推导过程可知:
(1)直线l上每一个点的坐标(x,y)都满足关系式;
(2)坐标满足关系式的每一个点都在直线l上.
新知讲解
问题4 你可以解释下为什么坐标满足关系式的每一个点都在直线上?
若点的坐标,满足关系式,则,
(1)当时,这时点与重合,显然有点在直线l上;
(2)当时,有,这表明过点,的直线l的斜率为. 因为直线的斜率都为,且都过点P,所以它们重合.所以,点在直线l上.
概念生成
我们把方程称为过点,斜率为k的直线的方程。叫做直线的点斜式方程,简称点斜式.
定点
直线的斜率
坐标满足关系式的点一定在直线上;
直线上任意一点的坐标一定满足关系式.
新知探究
探究二:过点且倾斜角为0°或90°的直线方程
合作探究
(1)当直线的倾斜角为0°时,直线的方程是什么?为什么?
(2)当直线的倾斜角为90°时,直线的方程是什么?为什么?
新知讲解
当直线的倾斜角为时,,即,这时直线l与x轴平行或重合,直线的方程是,即.
新知讲解
当直线的倾斜角为时,由于无意义,直线没有斜率,这时直线与轴平行或重合,它的方程不能用点斜式表示.又因为这时直线上每一点的横坐标都等于,所以它的方程是
,即.
课堂练习
例1 直线经过点,且倾斜角,求直线的点斜式方程,并画出直线
解:直线经过点(-2,3),斜率
,代入点斜式方程得:
.
两点确定一条直线,所以再找一个点即可!
新知探究
探究三:直线的斜截式方程
新知讲解
问题5 下面我们来看点斜式的一种特殊情况:如果斜率为的直线过点,这时 是直线与轴的交点,此时方程如何表示?
将代入直线的点斜式方程,得
概念生成
我们把直线与轴的交点()的纵坐标叫做直线在轴上的截距.这样,方程由直线的斜率k与它在轴上的截距b确定,我们把方程叫做直线的斜截式方程,简称斜截式.
和的几何意义:是直线的斜率,是直线在轴上的截距.
新知讲解
问题6 方程与我们学过的一次函数表达式类似.我们知道,一次函数的图象是一条直线,你如何从直线方程的角度认识一次函数?你能说出一次函数,及图象的特点吗?
对于,从函数的角度看,它表示的是自变量α与因变量y之间的对应关系,
而从直线方程的角度看,它表示的是平面直角坐标系中一条直线上点的坐标所满足的代数关系.
一次函数,及的图象所对应的三条直线,它们的斜率不同,分别为2,3,;它们在y轴上的截距也不同,分别为1,0,3.
课堂练习
例2 已知直线:,: ,试讨论:
(1)的条件是什么
(2) 的条件是什么
解:(1)若,则=,此时,与y轴的交点不同,即≠;反之,若=,且≠,则.
(2)若,则;反之,若,则.
方法小结
对于直线:,: ,
,且≠;
.
只有斜率相等不能保证直线平行,还要说明它们过两个不同的点,否则有可能重合.
随堂练习
1.写出下列直线的点斜式方程:
(1)经过点A(3,),斜率是;
(2)经过点B(,2),倾斜角是30°;
(3)经过点C(0,3),倾斜角是0°;
(4)经过点D,倾斜角是.
解析:(1)
(2),
(3),.
(4),
新知探究
3.写出下列直线的斜截式方程;
(1)斜率是,在y轴上的截距是;
(2)斜率是,在y轴上的截距是4.
小结
1.直线的点斜式方程
由直线上一个定点及该直线的斜率k确定
2.直线的斜截式方程
方程
和的几何意义:是直线的斜率,是直线在轴上的截距.
2.2直线的方程
直线和圆的方程
2.2.1直线的点斜式方程
课程标准
在平面直角坐标系中,根据确定直线位置的几何要素(点+斜率),探索直线的点斜式方程,并掌握直线的点斜式方程。
复习回顾
问题1 如何求直线的斜率?
问题2 如何判断直线的平行与垂直?
通过直线斜率进行判断
l1//l2=.
l1l2=1.
新课导入
导
问题2 如何确定一条直线?
已知两点可以确定一条直线。
已知直线上的一点和直线的倾斜角(斜率)可以确定一条直线。
这样,在平面直角坐标系中,给定一个点和斜率k(或倾斜角),就能唯一确定一条直线.也就是说,这条直线上任意一点的坐标(x,y)与点的坐标和斜率k之间的关系是完全确定的。
那么,我们下面来探究点和斜率k(或倾斜角)之间的关系
一
二
三
教学目标
了解由斜率公式推导直线方程的点斜式的过程
掌握直线的点斜式方程和斜截式方程,并会用它们求直线的方程
会利用直线的点斜式和斜截式方程解决有关的问题
教学目标
难点
重点
新知探究
探究一:过点且斜率为k(或倾斜角为)的直线方程
新知讲解
如图,直线经过点,且斜率为.设是直线上不同于点的任意一点,因为直线l的斜率为k,由斜率公式得
(x,y)
即
追问:点的坐标满足关系式吗?
新知讲解
问题3 直线上的点满足关系式吗?
(x,y)
答案是肯定的!
推导过程可知:
(1)直线l上每一个点的坐标(x,y)都满足关系式;
(2)坐标满足关系式的每一个点都在直线l上.
新知讲解
问题4 你可以解释下为什么坐标满足关系式的每一个点都在直线上?
若点的坐标,满足关系式,则,
(1)当时,这时点与重合,显然有点在直线l上;
(2)当时,有,这表明过点,的直线l的斜率为. 因为直线的斜率都为,且都过点P,所以它们重合.所以,点在直线l上.
概念生成
我们把方程称为过点,斜率为k的直线的方程。叫做直线的点斜式方程,简称点斜式.
定点
直线的斜率
坐标满足关系式的点一定在直线上;
直线上任意一点的坐标一定满足关系式.
新知探究
探究二:过点且倾斜角为0°或90°的直线方程
合作探究
(1)当直线的倾斜角为0°时,直线的方程是什么?为什么?
(2)当直线的倾斜角为90°时,直线的方程是什么?为什么?
新知讲解
当直线的倾斜角为时,,即,这时直线l与x轴平行或重合,直线的方程是,即.
新知讲解
当直线的倾斜角为时,由于无意义,直线没有斜率,这时直线与轴平行或重合,它的方程不能用点斜式表示.又因为这时直线上每一点的横坐标都等于,所以它的方程是
,即.
课堂练习
例1 直线经过点,且倾斜角,求直线的点斜式方程,并画出直线
解:直线经过点(-2,3),斜率
,代入点斜式方程得:
.
两点确定一条直线,所以再找一个点即可!
新知探究
探究三:直线的斜截式方程
新知讲解
问题5 下面我们来看点斜式的一种特殊情况:如果斜率为的直线过点,这时 是直线与轴的交点,此时方程如何表示?
将代入直线的点斜式方程,得
概念生成
我们把直线与轴的交点()的纵坐标叫做直线在轴上的截距.这样,方程由直线的斜率k与它在轴上的截距b确定,我们把方程叫做直线的斜截式方程,简称斜截式.
和的几何意义:是直线的斜率,是直线在轴上的截距.
新知讲解
问题6 方程与我们学过的一次函数表达式类似.我们知道,一次函数的图象是一条直线,你如何从直线方程的角度认识一次函数?你能说出一次函数,及图象的特点吗?
对于,从函数的角度看,它表示的是自变量α与因变量y之间的对应关系,
而从直线方程的角度看,它表示的是平面直角坐标系中一条直线上点的坐标所满足的代数关系.
一次函数,及的图象所对应的三条直线,它们的斜率不同,分别为2,3,;它们在y轴上的截距也不同,分别为1,0,3.
课堂练习
例2 已知直线:,: ,试讨论:
(1)的条件是什么
(2) 的条件是什么
解:(1)若,则=,此时,与y轴的交点不同,即≠;反之,若=,且≠,则.
(2)若,则;反之,若,则.
方法小结
对于直线:,: ,
,且≠;
.
只有斜率相等不能保证直线平行,还要说明它们过两个不同的点,否则有可能重合.
随堂练习
1.写出下列直线的点斜式方程:
(1)经过点A(3,),斜率是;
(2)经过点B(,2),倾斜角是30°;
(3)经过点C(0,3),倾斜角是0°;
(4)经过点D,倾斜角是.
解析:(1)
(2),
(3),.
(4),
新知探究
3.写出下列直线的斜截式方程;
(1)斜率是,在y轴上的截距是;
(2)斜率是,在y轴上的截距是4.
小结
1.直线的点斜式方程
由直线上一个定点及该直线的斜率k确定
2.直线的斜截式方程
方程
和的几何意义:是直线的斜率,是直线在轴上的截距.
