数学人教A版2019必修第一册5.6 函数y=Asin(ωx+φ) 课件(共43张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册5.6 函数y=Asin(ωx+φ) 课件(共43张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 15:59:28 | ||
图片预览




文档简介
(共43张PPT)
5.6函数y=Asin(ωx+φ)
5.6.1匀速圆周运动的数学模型
预备知识1:数学模型
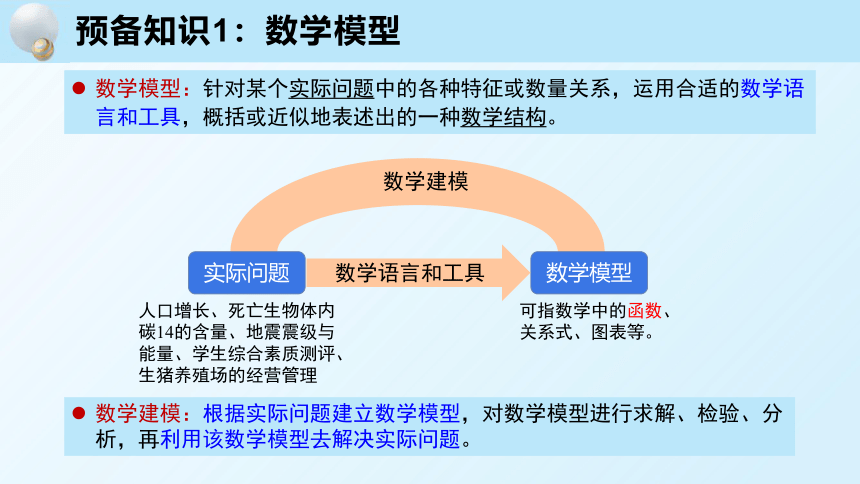
数学模型:针对某个实际问题中的各种特征或数量关系,运用合适的数学语言和工具,概括或近似地表述出的一种数学结构。
可指数学中的函数、关系式、图表等。
实际问题
数学模型
数学建模
人口增长、死亡生物体内碳14的含量、地震震级与能量、学生综合素质测评、生猪养殖场的经营管理
数学语言和工具
数学建模:根据实际问题建立数学模型,对数学模型进行求解、检验、分析,再利用该数学模型去解决实际问题。
预备知识2:三角函数的定义
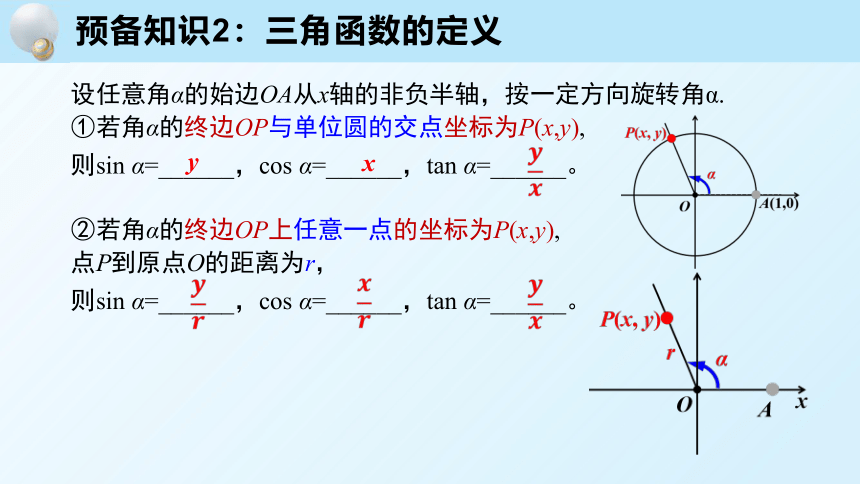
设任意角α的始边OA从x轴的非负半轴,按一定方向旋转角α.
①若角α的终边OP与单位圆的交点坐标为P(x,y),
则sin α=______,cos α=______,tan α=______。
y
x
②若角α的终边OP上任意一点的坐标为P(x,y),
点P到原点O的距离为r,
则sin α=______,cos α=______,tan α=______。
预备知识3:单位圆上的匀速圆周运动
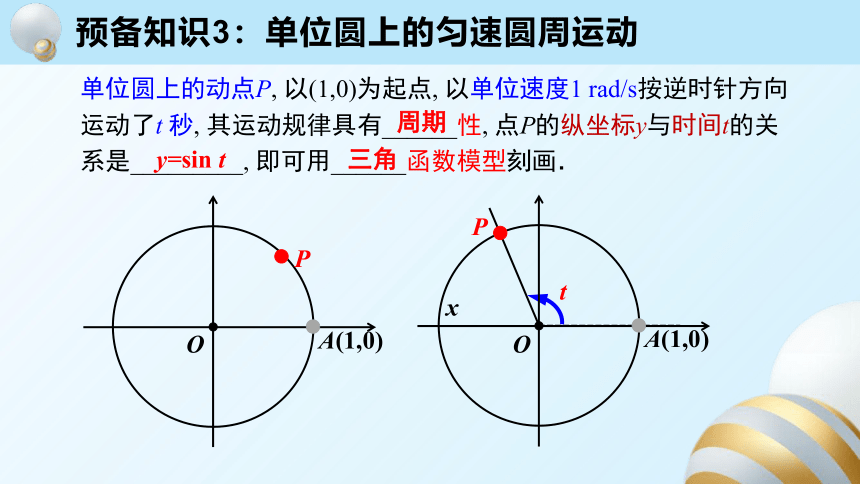
单位圆上的动点P, 以(1,0)为起点, 以单位速度1 rad/s按逆时针方向运动了t 秒, 其运动规律具有______性, 点P的纵坐标y与时间t的关系是_________, 即可用______函数模型刻画.
y=sin t
t
P
A(1,0)
O
x
三角
P
A(1,0)
O
周期
提出问题:一般的匀速圆周运动
生活中一般的匀速圆周运动与上述运动有什么异同点?
可用怎样的数学模型刻画?
摩天轮上的观光车厢
自行车轮上的某点
筒车上的盛水筒
不同:圆的半径、角速度、起点位置等
相同:周期性等
可用三角函数模型刻画
筒车是我国古代发明的一种以水流作动力,取水灌田的水利灌溉工具,它既节省人力,又经济环保。
轮周斜装若干竹木制的盛水筒,利用水流推动主轮时,轮周小筒按次序入水舀满, 至顶倾出, 接以木槽, 导入渠田。
实际问题
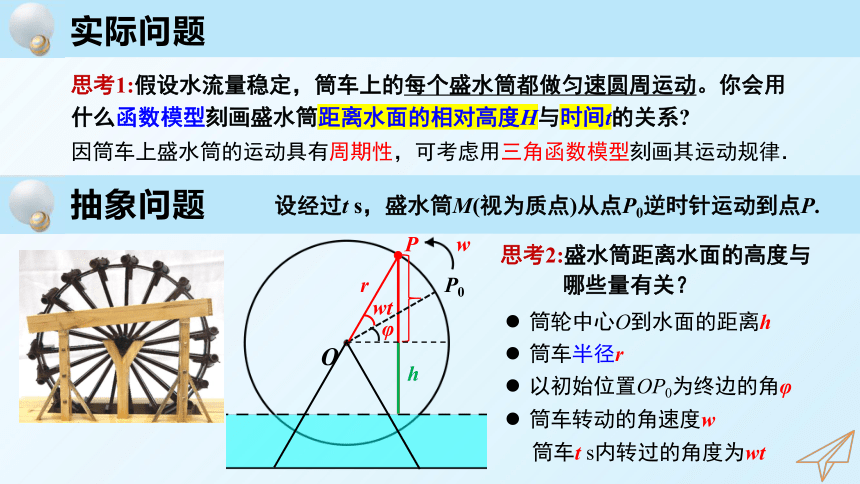
思考1:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动。你会用
什么函数模型刻画盛水筒距离水面的相对高度H与时间t的关系
因筒车上盛水筒的运动具有周期性,可考虑用三角函数模型刻画其运动规律.
实际问题
wt
抽象问题
思考2:盛水筒距离水面的高度与
哪些量有关?
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P.
P0
P
筒轮中心O到水面的距离h
筒车半径r
以初始位置OP0为终边的角φ
O
r
h
筒车转动的角速度w
w
φ
筒车t s内转过的角度为wt
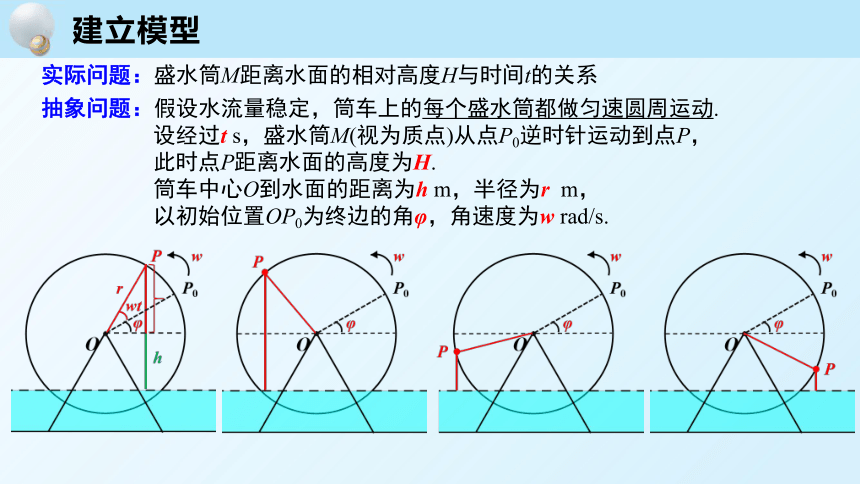
建立模型
抽象问题:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动.
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P,
此时点P距离水面的高度为H.
筒车中心O到水面的距离为h m,半径为r m,
以初始位置OP0为终边的角φ,角速度为w rad/s.
实际问题:盛水筒M距离水面的相对高度H与时间t的关系
抽象问题:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动.
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P,
此时点P距离水面的高度为H.
筒车中心O到水面的距离为h m,半径为r m,
以初始位置OP0为终边的角φ,角速度为w rad/s.
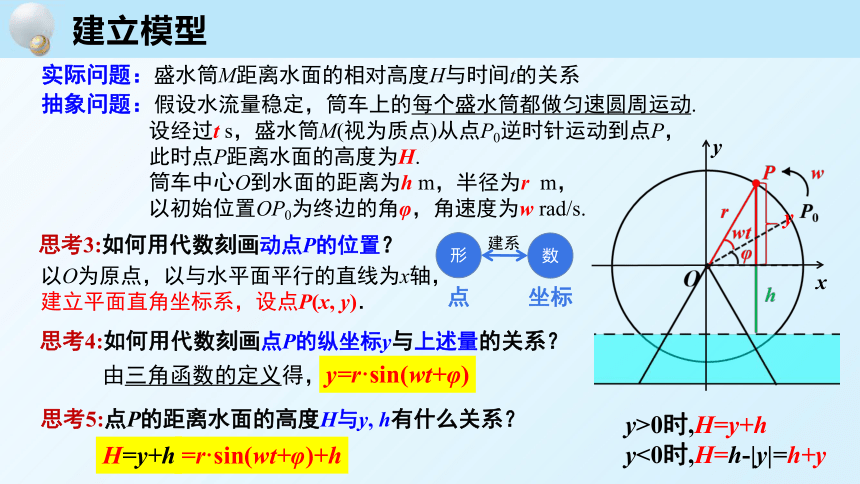
建立模型
思考3:如何用代数刻画动点P的位置?
以O为原点,以与水平面平行的直线为x轴,
建立平面直角坐标系,设点P(x, y).
x
y
思考4:如何用代数刻画点P的纵坐标y与上述量的关系?
y=r·sin(wt+φ)
由三角函数的定义得,
思考5:点P的距离水面的高度H与y, h有什么关系?
H=y+h
=r·sin(wt+φ)+h
形
数
点
坐标
建系
y>0时,H=y+h
y<0时,H=h-|y|=h+y
y
实际问题:盛水筒M距离水面的相对高度H与时间t的关系
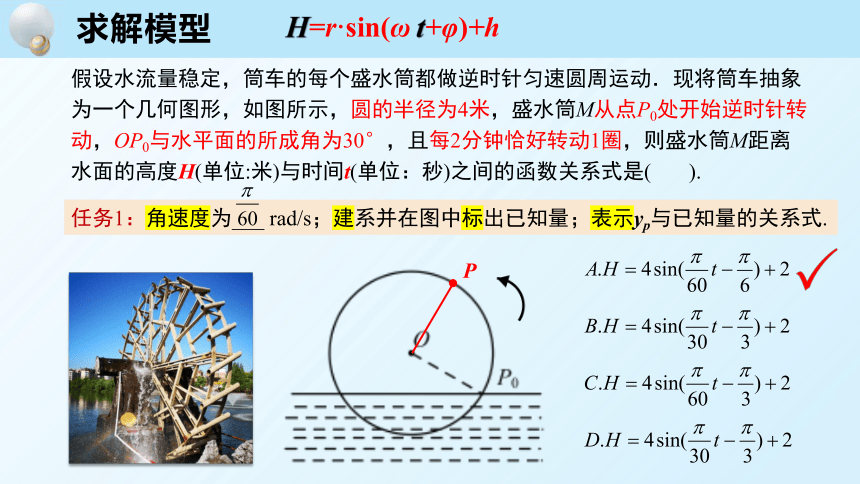
求解模型
假设水流量稳定,筒车的每个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒M从点P0处开始逆时针转动,OP0与水平面的所成角为30°,且每2分钟恰好转动1圈,则盛水筒M距离水面的高度H(单位:米)与时间t(单位:秒)之间的函数关系式是( ).
P
任务1:角速度为___ rad/s;建系并在图中标出已知量;表示yp与已知量的关系式.
H=r·sin(ωt+φ)+h
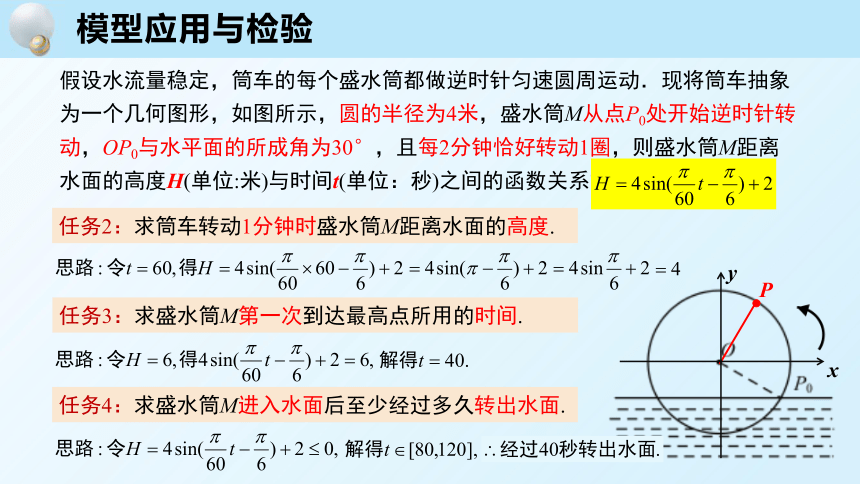
模型应用与检验
假设水流量稳定,筒车的每个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒M从点P0处开始逆时针转动,OP0与水平面的所成角为30°,且每2分钟恰好转动1圈,则盛水筒M距离水面的高度H(单位:米)与时间t(单位:秒)之间的函数关系式是
P
任务2:求筒车转动1分钟时盛水筒M距离水面的高度.
x
y
任务3:求盛水筒M第一次到达最高点所用的时间.
任务4:求盛水筒M进入水面后至少经过多久转出水面.
匀速圆周运动的
数学模型
实际
问题
抽象问题
建立模型
求解模型
模型应用
与检验
课堂小结
筒车的运动规律
筒车上的盛水筒做匀速圆周运动,研究盛水筒距离水面的高度H与时间t的关系。
画图,建系,找量
将需要用到的变量和常量代数化,数形结合。
建立函数模型
利用三角函数的定义、平面几何等数学工具来刻画各变量、常量间的数学关系。
H=r·sin(ωt+φ)+h
收集数据,求解模型
利用获取的数据资料,对模型的所有参数做出计算。
借助模型,解决实际问题
将模型计算经过与实际情形进行比较,以此验证模型的准确性和适用性。若模型与实际较吻合,则要对计算结果给出实际含义。
数学源于生活,用于生活!
数学建模是联系数学与实际问题的桥梁!
问题延伸与思考
2.本节课我们研究了筒车的盛水筒的运动规律,得出了一个新的函数模型:y=Asin(ωx+φ)+k,根据研究指数函数、对数函数等函数的经验,接下来应该研究什么?
y=Asin(ωx+φ)+k的图象和性质
1.若筒车上均匀分布着12个盛水筒,求相邻两个盛水筒的高度差的解析式,并利用已学的和差化积的方法或辅助角公式对该解析式进行变形化简,并求其最大值.
5.6.2函数y=Asin(ωx+φ)的图象
1.参数φ对y=sin(x+φ)的图象的影响
2.参数ω对y=sin(ωx+φ)图象的影响(ω>0)
3.参数A对y=Asin(ωx+φ)图象的影响(A>0)
方法梳理:y=Asin(ωx+φ)的图象
(法1:先平移后伸缩)
(法2:先伸缩后平移)
运用:y=Asin(ωx+φ)的图象
P239
画简图
标五点
运用:y=Asin(ωx+φ)的图象
P239
运用:y=Asin(ωx+φ)的图象
P239
运用:y=Asin(ωx+φ)的图象
P239
[变式]P240-1 C A D
y=Asin(ωx+φ)的图象
y=Asin(ωx+φ)的性质(A>0)
(原理:令y=±A,三角函数在对称轴取得最值)
(原理:令y=0)
▲求指定区间上的值域
y=Asin(ωx+φ)的性质(A>0)
运算易出错,注意检查
y=Atan(ωx+φ)的性质(A>0)
▲求指定区间上的值域
课后作业
1.课本P240-2(3)(4)、P255-第21、22题
提示:二倍角公式、辅助角公式、结合y=sin t的图象
三角函数的图象和性质
综合运用
要点1:由图象求解析式/求值
(法1:代最值点)
(代特殊点)
要点1:由图象求解析式/求值
(法2:代零点)
(代特殊点)
A:看最值
w:看周期
φ:代最值点
代零点:需区分“升零点”or“降零点”.
要点1:由图象求解析式/求值
(代最值点)
要点1:由图象求解析式/求值
(代最值点)
要点1:由图象求解析式/求值
要点2:由解析式定性质
BCD
(0,1)是递增时的点
要点3:知性质求参数(ω)
(法1)
(法2)
要点3:知性质求参数(ω)
(法1)
(法2)
要点3:知性质求参数(ω)
析:
B
要点4:知性质求参数(ω)
析:
A
法2:特殊值排除法
2
-2
要点5:图象与交点(零点)问题
方程的解
图象的交点
要点5:图象与交点(零点)问题
方程的解
图象的交点
换元
2
-2
Thanks
好学数学
数学好学
学好数学
hào
hǎo
hǎo
5.6函数y=Asin(ωx+φ)
5.6.1匀速圆周运动的数学模型
预备知识1:数学模型
数学模型:针对某个实际问题中的各种特征或数量关系,运用合适的数学语言和工具,概括或近似地表述出的一种数学结构。
可指数学中的函数、关系式、图表等。
实际问题
数学模型
数学建模
人口增长、死亡生物体内碳14的含量、地震震级与能量、学生综合素质测评、生猪养殖场的经营管理
数学语言和工具
数学建模:根据实际问题建立数学模型,对数学模型进行求解、检验、分析,再利用该数学模型去解决实际问题。
预备知识2:三角函数的定义
设任意角α的始边OA从x轴的非负半轴,按一定方向旋转角α.
①若角α的终边OP与单位圆的交点坐标为P(x,y),
则sin α=______,cos α=______,tan α=______。
y
x
②若角α的终边OP上任意一点的坐标为P(x,y),
点P到原点O的距离为r,
则sin α=______,cos α=______,tan α=______。
预备知识3:单位圆上的匀速圆周运动
单位圆上的动点P, 以(1,0)为起点, 以单位速度1 rad/s按逆时针方向运动了t 秒, 其运动规律具有______性, 点P的纵坐标y与时间t的关系是_________, 即可用______函数模型刻画.
y=sin t
t
P
A(1,0)
O
x
三角
P
A(1,0)
O
周期
提出问题:一般的匀速圆周运动
生活中一般的匀速圆周运动与上述运动有什么异同点?
可用怎样的数学模型刻画?
摩天轮上的观光车厢
自行车轮上的某点
筒车上的盛水筒
不同:圆的半径、角速度、起点位置等
相同:周期性等
可用三角函数模型刻画
筒车是我国古代发明的一种以水流作动力,取水灌田的水利灌溉工具,它既节省人力,又经济环保。
轮周斜装若干竹木制的盛水筒,利用水流推动主轮时,轮周小筒按次序入水舀满, 至顶倾出, 接以木槽, 导入渠田。
实际问题
思考1:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动。你会用
什么函数模型刻画盛水筒距离水面的相对高度H与时间t的关系
因筒车上盛水筒的运动具有周期性,可考虑用三角函数模型刻画其运动规律.
实际问题
wt
抽象问题
思考2:盛水筒距离水面的高度与
哪些量有关?
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P.
P0
P
筒轮中心O到水面的距离h
筒车半径r
以初始位置OP0为终边的角φ
O
r
h
筒车转动的角速度w
w
φ
筒车t s内转过的角度为wt
建立模型
抽象问题:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动.
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P,
此时点P距离水面的高度为H.
筒车中心O到水面的距离为h m,半径为r m,
以初始位置OP0为终边的角φ,角速度为w rad/s.
实际问题:盛水筒M距离水面的相对高度H与时间t的关系
抽象问题:假设水流量稳定,筒车上的每个盛水筒都做匀速圆周运动.
设经过t s,盛水筒M(视为质点)从点P0逆时针运动到点P,
此时点P距离水面的高度为H.
筒车中心O到水面的距离为h m,半径为r m,
以初始位置OP0为终边的角φ,角速度为w rad/s.
建立模型
思考3:如何用代数刻画动点P的位置?
以O为原点,以与水平面平行的直线为x轴,
建立平面直角坐标系,设点P(x, y).
x
y
思考4:如何用代数刻画点P的纵坐标y与上述量的关系?
y=r·sin(wt+φ)
由三角函数的定义得,
思考5:点P的距离水面的高度H与y, h有什么关系?
H=y+h
=r·sin(wt+φ)+h
形
数
点
坐标
建系
y>0时,H=y+h
y<0时,H=h-|y|=h+y
y
实际问题:盛水筒M距离水面的相对高度H与时间t的关系
求解模型
假设水流量稳定,筒车的每个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒M从点P0处开始逆时针转动,OP0与水平面的所成角为30°,且每2分钟恰好转动1圈,则盛水筒M距离水面的高度H(单位:米)与时间t(单位:秒)之间的函数关系式是( ).
P
任务1:角速度为___ rad/s;建系并在图中标出已知量;表示yp与已知量的关系式.
H=r·sin(ωt+φ)+h
模型应用与检验
假设水流量稳定,筒车的每个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒M从点P0处开始逆时针转动,OP0与水平面的所成角为30°,且每2分钟恰好转动1圈,则盛水筒M距离水面的高度H(单位:米)与时间t(单位:秒)之间的函数关系式是
P
任务2:求筒车转动1分钟时盛水筒M距离水面的高度.
x
y
任务3:求盛水筒M第一次到达最高点所用的时间.
任务4:求盛水筒M进入水面后至少经过多久转出水面.
匀速圆周运动的
数学模型
实际
问题
抽象问题
建立模型
求解模型
模型应用
与检验
课堂小结
筒车的运动规律
筒车上的盛水筒做匀速圆周运动,研究盛水筒距离水面的高度H与时间t的关系。
画图,建系,找量
将需要用到的变量和常量代数化,数形结合。
建立函数模型
利用三角函数的定义、平面几何等数学工具来刻画各变量、常量间的数学关系。
H=r·sin(ωt+φ)+h
收集数据,求解模型
利用获取的数据资料,对模型的所有参数做出计算。
借助模型,解决实际问题
将模型计算经过与实际情形进行比较,以此验证模型的准确性和适用性。若模型与实际较吻合,则要对计算结果给出实际含义。
数学源于生活,用于生活!
数学建模是联系数学与实际问题的桥梁!
问题延伸与思考
2.本节课我们研究了筒车的盛水筒的运动规律,得出了一个新的函数模型:y=Asin(ωx+φ)+k,根据研究指数函数、对数函数等函数的经验,接下来应该研究什么?
y=Asin(ωx+φ)+k的图象和性质
1.若筒车上均匀分布着12个盛水筒,求相邻两个盛水筒的高度差的解析式,并利用已学的和差化积的方法或辅助角公式对该解析式进行变形化简,并求其最大值.
5.6.2函数y=Asin(ωx+φ)的图象
1.参数φ对y=sin(x+φ)的图象的影响
2.参数ω对y=sin(ωx+φ)图象的影响(ω>0)
3.参数A对y=Asin(ωx+φ)图象的影响(A>0)
方法梳理:y=Asin(ωx+φ)的图象
(法1:先平移后伸缩)
(法2:先伸缩后平移)
运用:y=Asin(ωx+φ)的图象
P239
画简图
标五点
运用:y=Asin(ωx+φ)的图象
P239
运用:y=Asin(ωx+φ)的图象
P239
运用:y=Asin(ωx+φ)的图象
P239
[变式]P240-1 C A D
y=Asin(ωx+φ)的图象
y=Asin(ωx+φ)的性质(A>0)
(原理:令y=±A,三角函数在对称轴取得最值)
(原理:令y=0)
▲求指定区间上的值域
y=Asin(ωx+φ)的性质(A>0)
运算易出错,注意检查
y=Atan(ωx+φ)的性质(A>0)
▲求指定区间上的值域
课后作业
1.课本P240-2(3)(4)、P255-第21、22题
提示:二倍角公式、辅助角公式、结合y=sin t的图象
三角函数的图象和性质
综合运用
要点1:由图象求解析式/求值
(法1:代最值点)
(代特殊点)
要点1:由图象求解析式/求值
(法2:代零点)
(代特殊点)
A:看最值
w:看周期
φ:代最值点
代零点:需区分“升零点”or“降零点”.
要点1:由图象求解析式/求值
(代最值点)
要点1:由图象求解析式/求值
(代最值点)
要点1:由图象求解析式/求值
要点2:由解析式定性质
BCD
(0,1)是递增时的点
要点3:知性质求参数(ω)
(法1)
(法2)
要点3:知性质求参数(ω)
(法1)
(法2)
要点3:知性质求参数(ω)
析:
B
要点4:知性质求参数(ω)
析:
A
法2:特殊值排除法
2
-2
要点5:图象与交点(零点)问题
方程的解
图象的交点
要点5:图象与交点(零点)问题
方程的解
图象的交点
换元
2
-2
Thanks
好学数学
数学好学
学好数学
hào
hǎo
hǎo
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
