数学人教A版2019必修第一册5.1 任意角和弧度制 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册5.1 任意角和弧度制 课件(共33张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 16:03:48 | ||
图片预览









文档简介
(共33张PPT)
第五章《三角函数》
5.1.1 任意角
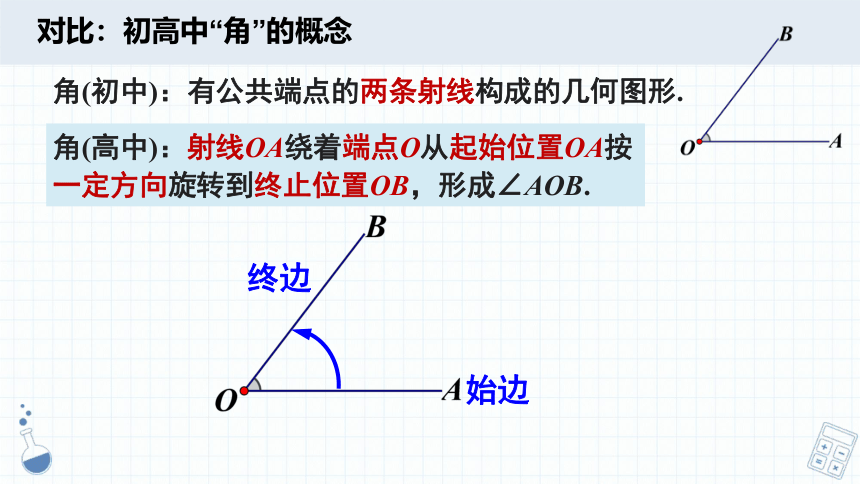
对比:初高中“角”的概念
角(高中):射线OA绕着端点O从起始位置OA按一定方向旋转到终止位置OB,形成∠AOB.
始边
终边
角(初中):有公共端点的两条射线构成的几何图形.
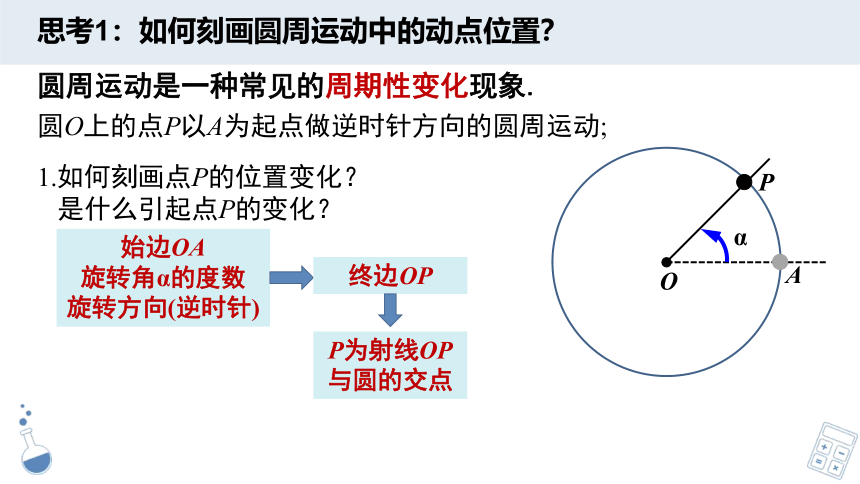
思考1:如何刻画圆周运动中的动点位置?
圆周运动是一种常见的周期性变化现象.
P
A
O
圆O上的点P以A为起点做逆时针方向的圆周运动;
1.如何刻画点P的位置变化?
是什么引起点P的变化?
始边OA
旋转角α的度数
旋转方向(逆时针)
终边OP
P为射线OP
与圆的交点
α
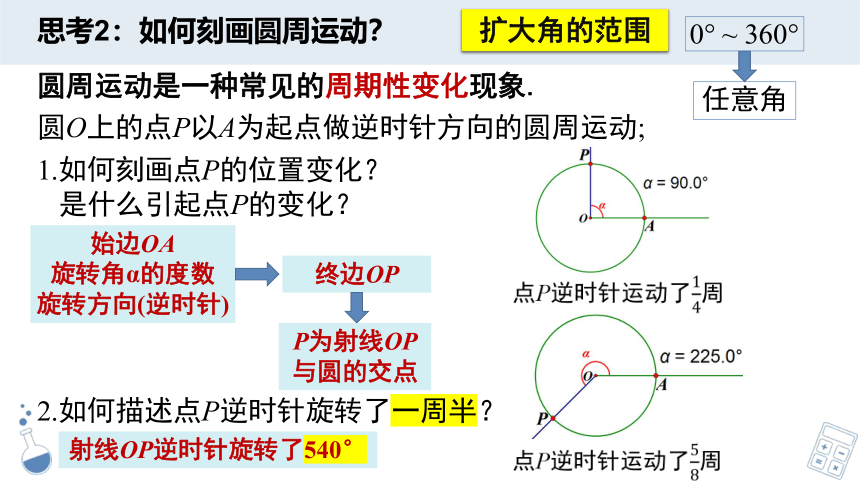
思考2:如何刻画圆周运动?
圆周运动是一种常见的周期性变化现象.
圆O上的点P以A为起点做逆时针方向的圆周运动;
1.如何刻画点P的位置变化?
是什么引起点P的变化?
始边OA
旋转角α的度数
旋转方向(逆时针)
终边OP
P为射线OP
与圆的交点
2.如何描述点P逆时针旋转了一周半?
射线OP逆时针旋转了540°
扩大角的范围
任意角
生活中的任意角
时钟慢了1小时10分钟,
校准时分针要___时针旋转____°
顺
420
体操运动员单手侧空翻转体540°
体操运动员前空翻转体720°
主动轮逆时针旋转80°
被动轮顺时针旋转80°
旋转的方向
旋转的度数
新知1:任意角的定义
正角:
负角:
一条射线绕其端点顺时针旋转形成的角.
如:α=﹣540 ,α=﹣120 .
一条射线绕其端点逆时针旋转形成的角.
如:α=60 ,α=425 .
零角:
一条射线没作任何旋转.
(零角的始边与终边重合)
任意角
已知一条射线的起始位置OA:
[注]①在不引起混淆的情况下,“角 ”或“∠ ”可以简写成“ ”;
②角的表示:A,B,C,…或α,β,θ,… ;
③角的“±”表示旋转方向:“﹢逆﹣顺” ( 与﹣ 互为相反角) ;
④角的加法:规定,把角α的终边旋转角β,此时终边对应的角是α+β.
⑤角的减法:α-β=α+(﹣β )
巩固:任意角的定义
①经过过1小时,时针旋转形成的角为30°.( )
②终边与始边重合的角是零角.( )
③小于90°的角是锐角.( )
[练习1]判断正误:
顺时针旋转30°,即为﹣30°
始边终边重合的角可为0°, 360°, 720°, -360°等,即k·360°
小于90°的角可为45°,-120°,0°等;
锐角是大于0°小于90°的角.
新知2:象限角的定义
我们通常在直角坐标系内讨论角。
使角的顶点与原点重合,角的始边与x轴非负半轴重合,则
角的终边在第几象限,就说该角是第几象限角。
如:α=﹣130°的终边在第三象限,则α是第三象限角.
锐角是第一象限角,钝角是第二象限角.
角的终边在坐标轴上,则认为此角不属于任何一个象限.
[练习2]已知A={第一象限的角},B={锐角},C={小于90 的角},
则下列正确的是( )
A. A=B=C
B. B∪C=A
C. A∩C=B
D. B∪C=C
D
新知3:终边相同的角
思考:在直角坐标系中,
给定一个角,则该角对应的终边唯一确定;
反之,若给定终边位置OB,则该终边对应的角唯一吗?
与45°终边相同的角为____________________
45°+k·360°(k∈Z)
y
x
o
45°
与角α终边相同的所有角组成的集合:
巩固:终边相同的角
判定α为第几象限角:先将其化为终边相同且在0°~360°内的角,再判断终边所在象限.
巩固:终边相同的角
例2.写出终边在y轴上的角的集合.
①终边在y轴正半轴的角的集合:
②终边在y轴负半轴的角的集合:
则终边在y轴上的角的集合:
[变式1]写出终边在x轴上的角的集合.
[变式2]写出终边在直线y=x上的角的集合.
巩固:象限角与终边相同的角
第一象限角:
第二象限角:
第三象限角:
第四象限角:
[练习3]若角α的终边在如图所示的阴影部分(包括边界),请指出角α的取值范围.
巩固:象限角与终边相同的角
D
C
y
x
巩固:象限角与终边相同的角
二等分
逆时针标1-4
三等分
第五章《三角函数》
5.1.2 弧度制
新知引入:多样的单位制
度量长度:米、英尺、码等单位制
度量重量:千克、磅等单位制
度量角:角度、……
角的度量是否也能用不同的单位制?
能否用十进制的实数来度量角?
度/分/秒的换算:六十进制 1度=60分 1分=60秒
角度制
角度(°)
实数
换算
探究:角度与弧长的关系
如图,对于同一圆心角α=60°,
若半径r不同,则所对圆弧长l也不同.
半径r r=1 r=2 r=3 r=4
圆弧长l
探究:角度与弧长的关系
如图,对于同一圆心角α=45°,
若半径r不同,则所对圆弧长l也不同.
半径r r=1 r=2 r=3 r=4
圆弧长l
探究:角度与弧长的关系
结论 : 同一圆心角α所对的圆弧长l与半径r之比为同一常数.
α的角度数
确定的常数l/r
称为“α的弧度数”
新知1:弧度制的定义
规定:长度等于半径的圆弧长所对的圆心角叫做1弧度的角,
记作1 rad表示,读作1弧度。
②今后用弧度制表示角时,“弧度”或“rad”可略去不写,如:α=1,β=2π
即:对于圆心角α,若l=r,则|α|=l/r=1 rad.
l=3r
|α|=l/r=3 rad
l=2πr
|α|=l/r=2π rad
正角的弧度数是正数
负角的弧度数是负数
零角的弧度数是0
新知1:弧度制的定义
规定:长度等于半径的圆弧长所对的圆心角叫做1弧度的角,
记作1 rad表示,读作1弧度。
即:对于圆心角α,若l=r,则|α|=l/r=1 rad.
弧度与角度的换算
新知2:弧度与角度的换算P174
角度(°)
弧度 (rad) 0
巩固:弧度与角度的换算P174
(3)与α终边相同的角的集合
(4)终边在直线y=x上的角的集合
注:角度和弧度不能混用
巩固:判断角的终边所在象限
二
三
二
课外知识——度量角的单位制
军事上还常用“密位制”
密位的写法是在百位上的数与十位上的数之间画一条短线“-”。如:
7密位:0-07(读作零,零七)
312密位:3-12
3000密位:30-00
007是风靡全球的一系列谍战电影。
007不仅是影片的名称,更是主人公特工詹姆斯·邦德的代号。
在故事里,邦德是英国情报机构军情六处的间谍,代号007,被授予可以除去任何妨碍行动的人的权力。
新知3:扇形计算公式的推导
新知3:扇形计算公式的推导
扇形的弧长:
扇形的面积:
新知3:扇形计算公式的运用
新知3:扇形计算公式的运用
已知一个扇形的周长为20cm,
(1)若扇形面积为9cm2,则该扇形的圆心角的弧度数是多少?
(2)当圆心角α的弧度数是多少时,该扇形面积最大?
新知3:扇形计算公式的运用
P176-12已知相互啮(niè)合的两个齿轮,大轮有48齿,小轮有20齿.
(1)当大轮转动1周时,小轮转动的角是____rad.
(2)如果大轮的转速为180 r/min(转/分),小轮的半径为10.5 cm,那么小轮周上一点每1 s转过的弧长是______cm.
大轮的转速为3 r/s(转/秒)
151.2π
151.2π
新知3:扇形计算公式的运用
谢 谢
第五章《三角函数》
5.1.1 任意角
对比:初高中“角”的概念
角(高中):射线OA绕着端点O从起始位置OA按一定方向旋转到终止位置OB,形成∠AOB.
始边
终边
角(初中):有公共端点的两条射线构成的几何图形.
思考1:如何刻画圆周运动中的动点位置?
圆周运动是一种常见的周期性变化现象.
P
A
O
圆O上的点P以A为起点做逆时针方向的圆周运动;
1.如何刻画点P的位置变化?
是什么引起点P的变化?
始边OA
旋转角α的度数
旋转方向(逆时针)
终边OP
P为射线OP
与圆的交点
α
思考2:如何刻画圆周运动?
圆周运动是一种常见的周期性变化现象.
圆O上的点P以A为起点做逆时针方向的圆周运动;
1.如何刻画点P的位置变化?
是什么引起点P的变化?
始边OA
旋转角α的度数
旋转方向(逆时针)
终边OP
P为射线OP
与圆的交点
2.如何描述点P逆时针旋转了一周半?
射线OP逆时针旋转了540°
扩大角的范围
任意角
生活中的任意角
时钟慢了1小时10分钟,
校准时分针要___时针旋转____°
顺
420
体操运动员单手侧空翻转体540°
体操运动员前空翻转体720°
主动轮逆时针旋转80°
被动轮顺时针旋转80°
旋转的方向
旋转的度数
新知1:任意角的定义
正角:
负角:
一条射线绕其端点顺时针旋转形成的角.
如:α=﹣540 ,α=﹣120 .
一条射线绕其端点逆时针旋转形成的角.
如:α=60 ,α=425 .
零角:
一条射线没作任何旋转.
(零角的始边与终边重合)
任意角
已知一条射线的起始位置OA:
[注]①在不引起混淆的情况下,“角 ”或“∠ ”可以简写成“ ”;
②角的表示:A,B,C,…或α,β,θ,… ;
③角的“±”表示旋转方向:“﹢逆﹣顺” ( 与﹣ 互为相反角) ;
④角的加法:规定,把角α的终边旋转角β,此时终边对应的角是α+β.
⑤角的减法:α-β=α+(﹣β )
巩固:任意角的定义
①经过过1小时,时针旋转形成的角为30°.( )
②终边与始边重合的角是零角.( )
③小于90°的角是锐角.( )
[练习1]判断正误:
顺时针旋转30°,即为﹣30°
始边终边重合的角可为0°, 360°, 720°, -360°等,即k·360°
小于90°的角可为45°,-120°,0°等;
锐角是大于0°小于90°的角.
新知2:象限角的定义
我们通常在直角坐标系内讨论角。
使角的顶点与原点重合,角的始边与x轴非负半轴重合,则
角的终边在第几象限,就说该角是第几象限角。
如:α=﹣130°的终边在第三象限,则α是第三象限角.
锐角是第一象限角,钝角是第二象限角.
角的终边在坐标轴上,则认为此角不属于任何一个象限.
[练习2]已知A={第一象限的角},B={锐角},C={小于90 的角},
则下列正确的是( )
A. A=B=C
B. B∪C=A
C. A∩C=B
D. B∪C=C
D
新知3:终边相同的角
思考:在直角坐标系中,
给定一个角,则该角对应的终边唯一确定;
反之,若给定终边位置OB,则该终边对应的角唯一吗?
与45°终边相同的角为____________________
45°+k·360°(k∈Z)
y
x
o
45°
与角α终边相同的所有角组成的集合:
巩固:终边相同的角
判定α为第几象限角:先将其化为终边相同且在0°~360°内的角,再判断终边所在象限.
巩固:终边相同的角
例2.写出终边在y轴上的角的集合.
①终边在y轴正半轴的角的集合:
②终边在y轴负半轴的角的集合:
则终边在y轴上的角的集合:
[变式1]写出终边在x轴上的角的集合.
[变式2]写出终边在直线y=x上的角的集合.
巩固:象限角与终边相同的角
第一象限角:
第二象限角:
第三象限角:
第四象限角:
[练习3]若角α的终边在如图所示的阴影部分(包括边界),请指出角α的取值范围.
巩固:象限角与终边相同的角
D
C
y
x
巩固:象限角与终边相同的角
二等分
逆时针标1-4
三等分
第五章《三角函数》
5.1.2 弧度制
新知引入:多样的单位制
度量长度:米、英尺、码等单位制
度量重量:千克、磅等单位制
度量角:角度、……
角的度量是否也能用不同的单位制?
能否用十进制的实数来度量角?
度/分/秒的换算:六十进制 1度=60分 1分=60秒
角度制
角度(°)
实数
换算
探究:角度与弧长的关系
如图,对于同一圆心角α=60°,
若半径r不同,则所对圆弧长l也不同.
半径r r=1 r=2 r=3 r=4
圆弧长l
探究:角度与弧长的关系
如图,对于同一圆心角α=45°,
若半径r不同,则所对圆弧长l也不同.
半径r r=1 r=2 r=3 r=4
圆弧长l
探究:角度与弧长的关系
结论 : 同一圆心角α所对的圆弧长l与半径r之比为同一常数.
α的角度数
确定的常数l/r
称为“α的弧度数”
新知1:弧度制的定义
规定:长度等于半径的圆弧长所对的圆心角叫做1弧度的角,
记作1 rad表示,读作1弧度。
②今后用弧度制表示角时,“弧度”或“rad”可略去不写,如:α=1,β=2π
即:对于圆心角α,若l=r,则|α|=l/r=1 rad.
l=3r
|α|=l/r=3 rad
l=2πr
|α|=l/r=2π rad
正角的弧度数是正数
负角的弧度数是负数
零角的弧度数是0
新知1:弧度制的定义
规定:长度等于半径的圆弧长所对的圆心角叫做1弧度的角,
记作1 rad表示,读作1弧度。
即:对于圆心角α,若l=r,则|α|=l/r=1 rad.
弧度与角度的换算
新知2:弧度与角度的换算P174
角度(°)
弧度 (rad) 0
巩固:弧度与角度的换算P174
(3)与α终边相同的角的集合
(4)终边在直线y=x上的角的集合
注:角度和弧度不能混用
巩固:判断角的终边所在象限
二
三
二
课外知识——度量角的单位制
军事上还常用“密位制”
密位的写法是在百位上的数与十位上的数之间画一条短线“-”。如:
7密位:0-07(读作零,零七)
312密位:3-12
3000密位:30-00
007是风靡全球的一系列谍战电影。
007不仅是影片的名称,更是主人公特工詹姆斯·邦德的代号。
在故事里,邦德是英国情报机构军情六处的间谍,代号007,被授予可以除去任何妨碍行动的人的权力。
新知3:扇形计算公式的推导
新知3:扇形计算公式的推导
扇形的弧长:
扇形的面积:
新知3:扇形计算公式的运用
新知3:扇形计算公式的运用
已知一个扇形的周长为20cm,
(1)若扇形面积为9cm2,则该扇形的圆心角的弧度数是多少?
(2)当圆心角α的弧度数是多少时,该扇形面积最大?
新知3:扇形计算公式的运用
P176-12已知相互啮(niè)合的两个齿轮,大轮有48齿,小轮有20齿.
(1)当大轮转动1周时,小轮转动的角是____rad.
(2)如果大轮的转速为180 r/min(转/分),小轮的半径为10.5 cm,那么小轮周上一点每1 s转过的弧长是______cm.
大轮的转速为3 r/s(转/秒)
151.2π
151.2π
新知3:扇形计算公式的运用
谢 谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
