第24章《解直角三角形》单元测试卷(困难)(含答案)
文档属性
| 名称 | 第24章《解直角三角形》单元测试卷(困难)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 521.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 09:38:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
华师大版初中数学九年级上册第24章《解直角三角形》单元测试卷
考试范围:第24章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图,在一斜边长的直角三角形木板即中截取一个正方形,点在边上,点在斜边上,点在边上,若::,则这块木板截取正方形后,剩余部分的面积为( )
A. B. C. D.
如图,一个斜边长为的红色直角三角形纸片,一个斜边长为的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红、蓝两张纸片的面积之和是( )
A. B. C. D.
如图,有一块直角边,的的铁片,现要把它加工成一个正方形加工中的损耗忽略不计,则正方形的边长为( )
A. B. C. D.
在 中,、、,于点,点、分别是、的中点,连接、、、,则下列结论错误的是( )
A. B.
C. D.
如图,四边形中.,,为的平分线,,、分别是、的中点,则的长为( )
A. B. C. D.
如图,在中,,,点在上,且,点是上的动点,连结,点,分别是和的中点,连结,,当时,线段长为( )
A. B. C. D.
如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形,连结并延长交于点若,则的长为( )
A. B.
C. D.
如图,在矩形中,,,点,分别是边,上的动点,点不与,重合,且,是五边形内一点,且.
点为中点时,
点到,的距离一定相等
点到边的距离最大为
点到边的距离可能为
则以上说法正确的个数是( )
A. 个 B. 个 C. 个 D. 个
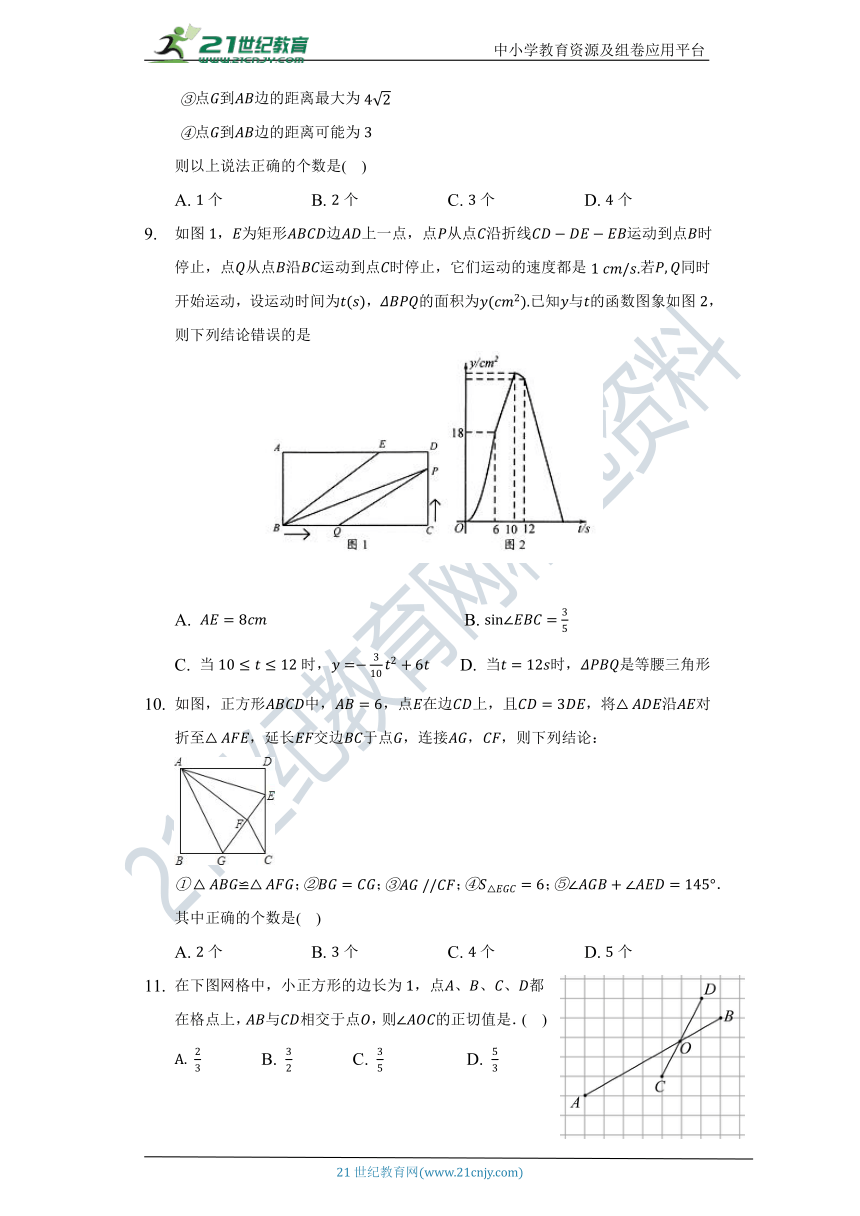
如图,为矩形边上一点,点从点沿折线运动到点时停止,点从点沿运动到点时停止,它们运动的速度都是若同时开始运动,设运动时间为,的面积为已知与的函数图象如图,则下列结论错误的是
A. B.
C. 当时, D. 当时,是等腰三角形
如图,正方形中,,点在边上,且,将沿对折至,延长交边于点,连接,,则下列结论:
≌;;;;.
其中正确的个数是( )
A. 个 B. 个 C. 个 D. 个
在下图网格中,小正方形的边长为,点、、、都在格点上,与相交于点,则的正切值是.( )
B. C. D.
如图,在矩形中,是边的中点,,垂足为点,连接,有下列五个结论:∽;;;;::其中正确结论的个数是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图所示的是古代一种可以远程攻击的投石车,图是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点,重锤挂在点,点为支点,点是水平底板上的一点,米,米.
投石车准备时,点恰好与点重合,此时和垂直,则______米.
投石车投石瞬间,的延长线交线段于点,若::,则点的上升高度为______米.
如图,在以为斜边的两个直角和中,,,,则______.
如图,在中,,,,点是边上一动点.连接,将沿折叠,点落在处,当点在内部不含边界时,长度的取值范围是____.
如图,在正方形中,点,点,点分别在边上,边上,边上,将正方形纸片沿折叠,使点与点重合,连接,,,若,,下列结论:≌;四边形是菱形;;的周长是;其中正确的是______只填写序号.
三、解答题(本大题共9小题,共72分)
如图,一位同学想利用树影测量树的高度,他在某一时刻测得高为米的竹竿直立时影长为米,此时,因树靠近一幢建筑物,影子不全落在地面上有一部分影子落在了墙上处,他先测得落在墙上的影子高为米,又测得地面部分的影长为米,则他测得的树高应为多少米?
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点,在近岸取点和,使点、、共线且直线与河垂直,接着再过点且与垂直的直线上选择适当的点,确定与过点且垂直的直线的交点如果测得,,,求河的宽度.
阅读以下文字并解答问题:
在“测量物体的高度”活动中,某数学兴趣小组的名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为米的竹竿的影长为米,甲树的影长为米如图.
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上如图,墙壁上的影长为米,落在地面上的影长为米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上如图,测得此影子长为米,一级台阶高为米,落在地面上的影长为米.
小明:测得丁树落在地面上的影长为米,落在坡面上影长为米如图身高是的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为.
在横线上直接填写甲树的高度为______米.
画出测量乙树高度的示意图,并求出乙树的高度.
请选择丙树的高度为______
A.米米米米
你能计算出丁树的高度吗?试试看.
已知,点为平面内一点,于.
如图,直接写出和之间的数量关系____;
如图,过点作于点,求证:;
如图,在问的条件下,点、在上,连接、、,平分,平分,若,,求的度数.
如图,中,,为的中点,四边形为平行四边形,,相交于连接,.
试确定四边形的形状,并说明理由.
若,,求四边形的面积.
当满足什么条件时,四边形为正方形?请给予证明.
李想是一位善于思考的学生,在一次数学活动课上,他将一块含有的直角三角板摆放在一组平行线上展开探究.已知直线,直角三角板中,,,点为直线上一定点.将直角三角板绕点转动,当点在直线上时,点也恰好在直线上.
如图,求的度数;
如图,若点在直线上方,点在下方,与交于点,作的角平分线并反向延长与的角平分线交于点在直角三角板绕点转动的过程中,的度数是否保持不变?若不变,求出的度数;否则,请说明理由;
如图,直角三角板绕点转动,若点在直线,之间不含,上,点在下方,,分别与交于点,设,是否存在正整数和,使得若存在,请求出和的值;若不存在,请说明理由.
矩形中,,分别以,所在直线为轴,轴,建立如图所示的平面直角坐标系.是边上一个动点不与,重合,过点的反比例函数的图象与边交于点.
当点运动到边的中点时,求点的坐标;
连接,求的正切值;
如图,将沿折叠,点恰好落在边上的点处,求此时反比例函数的解析式.
在平面直角坐标系中,已知抛物线与轴分别交于、两点,且点在点的左侧.
求出点、的坐标.
记抛物线的顶点为,连接,,当为等腰直角三角形时,在抛物线上是否存在一点,使得若存在,请直接写出点的坐标若不存在,请说明理由.
如图,矩形中,,,点是的中点,点在的延长线上,且一动点从点出发,以每秒个单位长度的速度沿匀速运动,到达点后,立即以原速度沿返回;另一动点从点出发,以每秒个单位长度的速度沿射线匀速运动,点、同时出发,当两点相遇时停止运动,在点、的运动过程中,以为边作等边,使和矩形在射线的同侧.设运动的时间为秒.
当等边的边恰好经过点时,求运动时间的值;
在整个运动过程中,设等边和矩形重叠部分的面积为,请直接写出与之间的函数关系式和相应的自变量的取值范围;
设与矩形的对角线的交点为,是否存在这样的,使是等腰三角形?若存在,求出对应的的值;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了相似三角形的应用:常常构造“”型或“”型相似图,利用对应边成比例求相应线段的长.也考查了正方形的性质.
设,则,利用正方形的性质得,,再证明∽,利用相似比得到,所以,则,解得,然后用的面积减去正方形的面积得到剩余部分的面积.
【解答】
解:设,则,
四边形为正方形,
,,
,
∽,
,
,
在中,,
,解得,
,,
剩余部分的面积
故选:.
2.【答案】
【解析】
【分析】
本题考查了相似三角形的应用,正方形的性质,勾股定理,熟记相似三角形的性质并求出直角三角形的两直角边的关系是解题的关键,也是本题的难点标注字母,根据两直线平行,同位角相等可得,然后求出和相似,根据相似三角形对应边成比例求出,即,设,表示出,再表示出、,利用勾股定理列出方程求出的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
【解答】
解:如图
正方形的边
∽
∽
设,则,
在中,
即
解得
红、蓝两张纸片的面积之和
.
故选:.
3.【答案】
【解析】解:如图,中,,,
可知,
过点作,垂足为,交于.
,
.
,
,,
∽,
.
设,则有:,
解得,
故选:.
中,求出,过点作,垂足为,交于,三角形的面积公式求出的长度,由相似三角形的判定定理得出∽,设边长,根据相似三角形的对应边成比例求出的长度可得.
本题主要考查把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出边长,熟练掌握对应高的比等于相似比是关键.
4.【答案】
【解析】解:四边形是平行四边形,
,,,
点、分别是、的中点,
,,
,
,
四边形是平行四边形,
,
,
;故选项A不符合题意;
,
,
,
,
,,
,
,
四边形是平行四边形,
四边形是菱形,
,故选项B不符合题意;
延长,交延长线于,
四边形是平行四边形,
,
,
为中点,
,
在和中,
,
≌,
,,
,
,
,
,
,
故选项C不符合题意;
四边形是菱形,
,
,,
,故选项D符合题意;
故选:.
根据平行四边形的性质得到,,,根据三角形中位线的性质得到,,根据平行线的性质得到;故选项A不符合题意;根据菱形的判定定理得到四边形是菱形,根据菱形的性质得到,故选项B不符合题意;延长,交延长线于,根据全等三角形的性质得到,,求得,故选项C不符合题意;根据菱形的性质得到,推出,故选项D符合题意.
本题考查了平行四边形的性质,菱形的判定,平行线的性质,全等三角形的性质和判定,等腰三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.
5.【答案】
【解析】解:,
,
,.
,
,
,
为的平分线,
,
,
,
连接并延长交于,
,
,
是的中点,
,
在和中,
,
≌,
,,
,
是的中点,
.
故选:.
根据勾股定理得到,根据平行线的性质和角平分线的定义得到,求得,连接并延长交于,根据全等三角形的性质得到,,求得,根据三角形中位线定理即可得到结论.
此题考查了三角形的中位线定理,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
6.【答案】
【解析】解:如图,分别过点,作的垂线,垂足为,,过点作于点,
四边形是矩形,
,,
,,
,
又点和点分别是线段和的中点,
和分别是和的中位线,
,,
,,
,
,,
设,
,,
在中,,
在中,,
,
,
解得,即,
在中,.
故选:.
分别过点,作的垂线,垂足为,,过点作于点,由中位线定理及勾股定理可分别表示出线段和的长,建立等式可求出结论.
本题主要考查中位线定理,勾股定理等,构造中位线是解题过程中常见思路.
7.【答案】
【解析】
【分析】
本题考查了正方形的性质、勾股定理、锐角三角函数、等腰三角形的性质、正确作出辅助线是解决本题的关键.
由大正方形是由四个全等的直角三角形和一个小正方形组成,可得,可得,过点作于点,由三角形为等腰直角三角形可证得三角形也为等腰直角三角形,设,则,由,可解得,进而可得,即可求出
【解析】
解:由图可知,,
则,,
大正方形是由四个全等的直角三角形和一个小正方形组成,
故AE
则
则在中,有,
即
过点作于点,如图所示.
四边形为正方形,为对角线,
为等腰直角三角形,
,
故为等腰直角三角形.
设,则,
解得:.
8.【答案】
【解析】
【分析】
本题考查了矩形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、锐角三角函数、含角的直角三角形、角的计算等知识.
当点为中点时,作于点,首先利用矩形的性质和在直角三角形中若直角边等于斜边的一半知;然后利用等腰直角三角形的性质和角的和差计算即可求出,从而知结论正确;
证明即可知结论正确;
分析可知当时,点到的距离最大为值,利用等腰直角三角形性质即可知结论正确;
分析知点始终在上运动,且在由到的运动过程中,点到的距离越来越大,所以假设当点与点重合时距离最短,求出最短距离即可知结论错误.
【解答】
解:如图,当点为中点时,作于点,
由矩形中知
点为中点,,
,
在中,,,
,
,
且,
是等腰直角三角形,,
,
故结论正确;
如图,过点作于点,于点,则,
,,
,
,
由题知,
在和中,
,
,故结论正确;
是等腰直角三角形,,
,
分析可知当时,点到的距离最大,最大值为,故结论正确;
由题意可知,点始终在上运动,且在由到的运动过程中,点到的距离越来越大,所以假设当点与点重合时距离最短,如图,作,则,
由知,且,
,
点不与,重合,
点到的距离大于,故结论错误.
综上所述,结论正确.
故选C.
9.【答案】
【解析】解:观察图象可知:点在上运动的时间为,在上运动的时间为,点在上运动的时间为,
所以,,,
,
,
,故A正确,
在中,,,
,
,故B正确,
当时,点在上,,又易知此时的,
中边上的高,
,故C正确,
故选:.
由图中信息一一判断即可解决问题.
本题考查动点问题的函数图象,解题的关键是理解题意,读懂图象信息,灵活运用所学知识解决问题,是中考选择题中的压轴题.
10.【答案】
【解析】
【分析】
本题考查了翻折变换、全等三角形的判定与性质、正方形的性质,解决本题的关键是综合运用以上知识.
根据四边形是正方形,和翻折即可证明正确;
结合和翻折的性质,利用勾股定理可得,进而根据三角形内角和可得正确;
根据,的值即可判定正确;
根据
即可计算,可以判断错误;
根据已知求得,,即可判断错误.
【解答】
解:四边形是正方形,
,,
由翻折可知:
,,
,,
在和中,
≌,
所以正确;
≌,
,,
,
,
,
在中,,
,
,
根据勾股定理,得
,
即,
解得,
,
,
所以正确;
由得,,
由得≌,
,
,
是等腰三角形,
,
≌
,
,
,
,故正确,
,故正确
,,
又,
,
.
所以错误.
所以其中正确的是,一共个.
故选:.
11.【答案】
【解析】
【分析】
本题考查解直角三角形,平行线的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
如图取格点,连接,则过点作于利用面积法求出,再利用勾股定理求出即可解决问题.
【解答】
解:如图取格点,连接,则.
过点作于.
,,
,
,
,
,
,
故选A.
12.【答案】
【解析】解:在矩形中,,,,
,
,垂足为点,
,
,
∽,故正确;
,
∽,
,
为的中点,
,
,
,故正确;
过作,交于,则,
,
四边形为平行四边形,
,即为的中点,
为的中点,
,故正确;
根据已知条件无法判断,故无法得到,故错误;
设,则,
∽,
,
,
:::,
,
,
,
:::,故正确.
综上,正确个数有个.
故选:.
结合矩形的性质证明,,可证明;证明∽,利用相似三角形的性质可证明;过作,于,则,证明为的中点,可证明;根据已知条件无法证明;设,则,由相似三角形的性质可求解相关三角形的面积,进而可求得,即可证明.
本题主要考查相似三角形的判定与性质,矩形的性质,解直角三角形等知识的综合运用.
13.【答案】;
.
【解析】
【分析】
本题主要考查了等腰三角形的性质、相似三角形的性质与判定、勾股定理等,解题关键是正确作出辅助线构造直角三角形和相似三角形.
过作于,证明∽,得出,根据等腰三角形的性质和勾股定理求出、,即可进行解答;
过作于,过作于,根据等腰三角形性质结合已知条件和勾股定理分别求出和的长,再证明∽,,代入数据可计算出的长即为点上升的高度.
【解答】
解:过作于,
,
,
,
∽,
,
米,米,
米,
米,
,
米,
故答案为:;
过作于,过作于,则,
米,::,
米,
米,
米,
,
∽,
,
即,
米,
故G点上升的高度为米.
故答案为:.
14.【答案】
【解析】解:如图所示,取的中点,连接,,
,
,
又,,
,
,
是等边三角形,
,
,
,,
,,
即,,
,
中,,
故答案为:.
取的中点,连接,,依据直角三角形斜边上中线的性质,即可得到是等边三角形,进而得出,再根据三角形外角性质以及三角形内角和定理,即可得到的度数.
本题主要考查了直角三角形斜边上中线的性质,即在直角三角形中,斜边上的中线等于斜边的一半.解决问题的关键是利用三角形外角性质得到,.
15.【答案】
【解析】
【分析】
本题考查了翻折变换,勾股定理,锐角三角函数等知识,求出点落在和上时的值是本题的关键.由勾股定理可而且的长,分别求出当点落在上时和当点落在上时,的长,即可求解.
【解答】
解:,,,
,
当点落在上时,如图,
将沿折叠,点落在处,
,
,
,
当点落在上时,如图,过点作于,
将沿折叠,点落在处,
,
,
,
,
,
,
,
,,
,
当点在内部不含边界时,长度的取值范围为.
16.【答案】
【解析】解:根据题意可知:,,
在和中,
,
≌,故正确;
在正方形中,
,,
,
点在边上,
,
,
四边形是姜形,故错误;
如图,过点作于点,
,,
,
,
设,,
,,
,,
,,
,
,
,
在中,根据勾股定理得:
,
,
在中,根据勾股定理得:
,
,
,
整理得,
在中,根据勾股定理得:
,
,
整理得,
,
解得或舍去,
,
,,
,,,故正确;
,
,
的周长是,故错误;
如图,连接交于点,
垂直平分,
,
,
,
,故正确;
所以正确的结论有.
故答案为:.
根据折叠的性质可得≌即可判断正确;再根据正方形的性质可得,进而可以判断错误;过点作于点,则,,可得,设,,则,,根据勾股定理即可判断正确;再利用公股定理计算的周长是,进而可以判断错误;然后连接交于点,则垂直平分,利用勾股定理和锐角三角函数,可以判断正确.
本题主要考查了正方形的性质,图形的折叠,勾股定理,解直角三角形,熟练掌握正方形的性质,图形的折叠,勾股定理,正确作出辅助线,构造直角三角形是解题的关键.
17.【答案】解:如图,过点作于,
则四边形是矩形,
所以,米,
米,
由题意得,,
所以,米,
树高米.
【解析】过点作于,根据同时同地物高与影长成正比列比例式求出的长度,再根据矩形的对边相等可得,然后根据计算即可得解.
本题考查了相似三角形的应用,熟记同时同地物高与影长成正比并列出比例式是解题的关键,难点在于作辅助线构造出三角形.
18.【答案】解:根据题意得出:,
则∽,
故,
,,,
,
解得:,
河的宽度为米.
【解析】根据相似三角形的性质得出,进而代入求出即可.
此题主要考查了相似三角形的判定与性质,根据已知得出∽是解题关键.
19.【答案】解:;
如图:设为乙树的高度,米,
四边形是平行四边形,
米
由题意得:,
解得:米,
故乙树的高度米;
;
如图:设为丁树的高度,米,米,
四边形是平行四边形,
,
由题意得:,解得:米,
,解得米,
故AE米,
故丁树的高度米.
【解析】
【分析】
本题考查了相似三角形的应用,解题的关键是从复杂的数学问题中整理出三角形并利用相似三角形求解,考查了同学们的建模能力.
直接利用同一时刻物体的影长与实际高度比值不,变进而得出答案;
直接利用平行四边形的性质得出的长,进而得出答案;
首先画出基本图形,进而分别求出,的长,即可得出答案;
首先画出基本图形,进而分别求出,的长,即可得出答案.
【解答】
解:一根长为米的竹竿的影长为米,甲树的影长为米,
甲树的高度为:米.
故答案为:;
见答案;
如图,
设为丙树的高度,米,由题意得:,米,
则米,
四边形是平行四边形,
米,
又由题意得,
米,
米,
故选:.
见答案.
20.【答案】解:;
如图,过点作,
,
,即,
又,
,
,
,,
,
,
;
如图,过点作,
平分,平分,
,,
由可得,
,
设,,则
,,,,
,
,,
,
中,由,可得
,整理得:,
由,可得
,整理得:,
由解得,
,
.
【解析】
【分析】
本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角补角相等进行推导.余角和补角计算的应用常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.
根据平行线的性质以及直角三角形的性质进行证明即可;
先过点作,根据同角的余角相等,得出,再根据平行线的性质,得出,即可得到;
先过点作,根据角平分线的定义,得出,再设,,根据,可得,根据,可得,最后解方程组即可得到,进而得出.
【解答】
解:如图,,
,
,
,
,
故答案为:;
见答案;
见答案.
21.【答案】证明:平行四边形,
,,
为中点,
,
,,
四边形为平行四边形,
又,
,
,
故四边形为菱形;
在中,,,
,
为中点,也为的中点,
,
四边形的面积;
应添加条件.
证明:,为中点,
三线合一的性质,即.
四边形为平行四边形,四边形为平行四边形,
,.
四边形为正方形.对角线互相垂直且相等的四边形是正方形
【解析】由题意容易证明平行且等于,又知,所以得到四边形为菱形;
根据解三角形的知识求出和的长,然后根据菱形的面积公式求出四边形的面积;
应添加条件,证明且相等即可.
本题主要考查正方形的判定、菱形的判定与性质和勾股定理等知识点,此题是道综合体,有一定的难度,解答的关键还是要能熟练掌握各种四边形的基本性质.
22.【答案】解:
;
的度数不变.
平分,平分
,
又
.
过作,
又
,
存在原因如下:
当点在直线上时如图,
当点在直线上时如图,
点在直线,之间不含在,上
,
,
若,
则
,,为正整数
解得
,,或
当时,
当时,,不合题意,舍去
当时,
当时,.
综上所述,存在正整数,,,满足题意.
【解析】此题考查了平行线的性质,角的平分线,一元一次不等式组的应用,角的计算等.
根据平行线的性质,可得到,再根据,再根据代入可得到的度数;
根据角的平分线定义,平行线的性质可得到,再根据对顶角定义得到,进而得到,再使用平行线的性质即可得到的度数;
可分情况:当点在直线上时如图,;当点在直线上时如图,,列出相应的一元一次不等式组,再分别求得对应的和的值,根据实际进行讨论取合适的值.
23.【答案】解:,,
,,
是的中点,
,
在反比例函数图象上,
,
反比例函数的解析式为,
点的纵坐标为,
;
点的横坐标为,
,
,
的纵坐标为,
,
,
在中,,
如图,由知,,
,,
过点作于,
,,
,
由折叠知,,,,
,
,
,
∽,
,
,
,
在中,,
,
,
反比例函数解析式为.
【解析】此题是反比例函数综合题,主要考查了待定系数法,中点坐标公式,相似三角形的判定和性质,锐角三角函数,求出:是解本题的关键.
先确定出点坐标,进而得出点坐标,即可得出结论;
先确定出点的横坐标,进而表示出点的坐标,得出,同理表示出,即可得出结论;
先判断出∽,即可求出,最后用勾股定理求出,即可得出结论.
24.【答案】解:,,
令可得:,
解得:,,
点在点的左侧,
点的坐标为,点的坐标为;
由可知,且为抛物线的顶点,如图,过点作,则.
当为等腰直角三角形时,,,
点的坐标为,
,
点的坐标为.
将点代入中,得,
抛物线表达式为.
当时,则有,设点的坐标为,
过点作轴的垂线,进而有,
当时,即,
,
此方程无解;
当时,即,
,
,
解得,,
将时,;
将时,.
综上所述,点的坐标为或
【解析】本题主要考查了二次函数与等腰直角三角形、锐角三角函数的综合,熟练掌握二次函数的图象与性质以及等腰直角三角形的性质是解决本题的关键.
先将二次函数一般式化为交点式,再令得出关于的一元二次方程并求解,最后根据、的位置即可确定坐标;
先求出的长,再作出图象并过点作,根据直角三角形斜边上的中线等于斜边的一半可知,再根据等腰直角三角形的性质结合锐角三角函数的定义与可分别求得点、的坐标,从而利用待定系数法可确定二次函数解析式,进而设点的坐标为,过点作轴的垂线,根据锐角三角函数的定义与可得关于的含绝对值的方程,最后分类讨论解此含绝对值的方程即可解决问题.
25.【答案】解:如图,当边恰好经过点时,
是等边三角形,
,
,
在中,
,,
,
解得,即,
,
当边恰好经过点时,;
如图,过点作于,
当时,
,
,
,,
,
;
如图,当时,
,,
,
四边形是矩形,
,
∽,
,
,
,,,
;
如图,当时,
,,
,
,
,
;
当时,
,
高为:,
;
存在.
在中,,
,
,
,
或,
如图,当时,
过点作与,
则,
在中,
,即,
,
即或;
或;
如图,当时,,
,
,,
,
,即或,
或;
如图,当时,
,
,
点和点重合,
,
当刚开始时,,
当返回时,
,舍去,
综上所述当,,,,时,是等腰三角形.
【解析】此题是四边形的综合题目,主要涉及知识点矩形的性质和判定以及解直角三角形的知识和等腰三角形的判定.
当边恰好经过点时,由得,在中,根据三角函数求得的值;
根据运动的时间为不同的取值范围,求等边和矩形重叠部分的面积为的值,当时,重叠部分是直角梯形,面积等于梯形的面积,
当时,重叠部分是,当时,重叠部分是,当时,重叠部分是正三角形的面积;
当时,,在中,由即,得,即或,求出或;
当时,,又因为得到,再由,求出,即或,求出或;
当时,所以,得到点和点重合,从而求出的值.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
华师大版初中数学九年级上册第24章《解直角三角形》单元测试卷
考试范围:第24章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
如图,在一斜边长的直角三角形木板即中截取一个正方形,点在边上,点在斜边上,点在边上,若::,则这块木板截取正方形后,剩余部分的面积为( )
A. B. C. D.
如图,一个斜边长为的红色直角三角形纸片,一个斜边长为的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红、蓝两张纸片的面积之和是( )
A. B. C. D.
如图,有一块直角边,的的铁片,现要把它加工成一个正方形加工中的损耗忽略不计,则正方形的边长为( )
A. B. C. D.
在 中,、、,于点,点、分别是、的中点,连接、、、,则下列结论错误的是( )
A. B.
C. D.
如图,四边形中.,,为的平分线,,、分别是、的中点,则的长为( )
A. B. C. D.
如图,在中,,,点在上,且,点是上的动点,连结,点,分别是和的中点,连结,,当时,线段长为( )
A. B. C. D.
如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形,连结并延长交于点若,则的长为( )
A. B.
C. D.
如图,在矩形中,,,点,分别是边,上的动点,点不与,重合,且,是五边形内一点,且.
点为中点时,
点到,的距离一定相等
点到边的距离最大为
点到边的距离可能为
则以上说法正确的个数是( )
A. 个 B. 个 C. 个 D. 个
如图,为矩形边上一点,点从点沿折线运动到点时停止,点从点沿运动到点时停止,它们运动的速度都是若同时开始运动,设运动时间为,的面积为已知与的函数图象如图,则下列结论错误的是
A. B.
C. 当时, D. 当时,是等腰三角形
如图,正方形中,,点在边上,且,将沿对折至,延长交边于点,连接,,则下列结论:
≌;;;;.
其中正确的个数是( )
A. 个 B. 个 C. 个 D. 个
在下图网格中,小正方形的边长为,点、、、都在格点上,与相交于点,则的正切值是.( )
B. C. D.
如图,在矩形中,是边的中点,,垂足为点,连接,有下列五个结论:∽;;;;::其中正确结论的个数是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图所示的是古代一种可以远程攻击的投石车,图是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点,重锤挂在点,点为支点,点是水平底板上的一点,米,米.
投石车准备时,点恰好与点重合,此时和垂直,则______米.
投石车投石瞬间,的延长线交线段于点,若::,则点的上升高度为______米.
如图,在以为斜边的两个直角和中,,,,则______.
如图,在中,,,,点是边上一动点.连接,将沿折叠,点落在处,当点在内部不含边界时,长度的取值范围是____.
如图,在正方形中,点,点,点分别在边上,边上,边上,将正方形纸片沿折叠,使点与点重合,连接,,,若,,下列结论:≌;四边形是菱形;;的周长是;其中正确的是______只填写序号.
三、解答题(本大题共9小题,共72分)
如图,一位同学想利用树影测量树的高度,他在某一时刻测得高为米的竹竿直立时影长为米,此时,因树靠近一幢建筑物,影子不全落在地面上有一部分影子落在了墙上处,他先测得落在墙上的影子高为米,又测得地面部分的影长为米,则他测得的树高应为多少米?
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点,在近岸取点和,使点、、共线且直线与河垂直,接着再过点且与垂直的直线上选择适当的点,确定与过点且垂直的直线的交点如果测得,,,求河的宽度.
阅读以下文字并解答问题:
在“测量物体的高度”活动中,某数学兴趣小组的名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为米的竹竿的影长为米,甲树的影长为米如图.
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上如图,墙壁上的影长为米,落在地面上的影长为米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上如图,测得此影子长为米,一级台阶高为米,落在地面上的影长为米.
小明:测得丁树落在地面上的影长为米,落在坡面上影长为米如图身高是的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为.
在横线上直接填写甲树的高度为______米.
画出测量乙树高度的示意图,并求出乙树的高度.
请选择丙树的高度为______
A.米米米米
你能计算出丁树的高度吗?试试看.
已知,点为平面内一点,于.
如图,直接写出和之间的数量关系____;
如图,过点作于点,求证:;
如图,在问的条件下,点、在上,连接、、,平分,平分,若,,求的度数.
如图,中,,为的中点,四边形为平行四边形,,相交于连接,.
试确定四边形的形状,并说明理由.
若,,求四边形的面积.
当满足什么条件时,四边形为正方形?请给予证明.
李想是一位善于思考的学生,在一次数学活动课上,他将一块含有的直角三角板摆放在一组平行线上展开探究.已知直线,直角三角板中,,,点为直线上一定点.将直角三角板绕点转动,当点在直线上时,点也恰好在直线上.
如图,求的度数;
如图,若点在直线上方,点在下方,与交于点,作的角平分线并反向延长与的角平分线交于点在直角三角板绕点转动的过程中,的度数是否保持不变?若不变,求出的度数;否则,请说明理由;
如图,直角三角板绕点转动,若点在直线,之间不含,上,点在下方,,分别与交于点,设,是否存在正整数和,使得若存在,请求出和的值;若不存在,请说明理由.
矩形中,,分别以,所在直线为轴,轴,建立如图所示的平面直角坐标系.是边上一个动点不与,重合,过点的反比例函数的图象与边交于点.
当点运动到边的中点时,求点的坐标;
连接,求的正切值;
如图,将沿折叠,点恰好落在边上的点处,求此时反比例函数的解析式.
在平面直角坐标系中,已知抛物线与轴分别交于、两点,且点在点的左侧.
求出点、的坐标.
记抛物线的顶点为,连接,,当为等腰直角三角形时,在抛物线上是否存在一点,使得若存在,请直接写出点的坐标若不存在,请说明理由.
如图,矩形中,,,点是的中点,点在的延长线上,且一动点从点出发,以每秒个单位长度的速度沿匀速运动,到达点后,立即以原速度沿返回;另一动点从点出发,以每秒个单位长度的速度沿射线匀速运动,点、同时出发,当两点相遇时停止运动,在点、的运动过程中,以为边作等边,使和矩形在射线的同侧.设运动的时间为秒.
当等边的边恰好经过点时,求运动时间的值;
在整个运动过程中,设等边和矩形重叠部分的面积为,请直接写出与之间的函数关系式和相应的自变量的取值范围;
设与矩形的对角线的交点为,是否存在这样的,使是等腰三角形?若存在,求出对应的的值;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了相似三角形的应用:常常构造“”型或“”型相似图,利用对应边成比例求相应线段的长.也考查了正方形的性质.
设,则,利用正方形的性质得,,再证明∽,利用相似比得到,所以,则,解得,然后用的面积减去正方形的面积得到剩余部分的面积.
【解答】
解:设,则,
四边形为正方形,
,,
,
∽,
,
,
在中,,
,解得,
,,
剩余部分的面积
故选:.
2.【答案】
【解析】
【分析】
本题考查了相似三角形的应用,正方形的性质,勾股定理,熟记相似三角形的性质并求出直角三角形的两直角边的关系是解题的关键,也是本题的难点标注字母,根据两直线平行,同位角相等可得,然后求出和相似,根据相似三角形对应边成比例求出,即,设,表示出,再表示出、,利用勾股定理列出方程求出的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
【解答】
解:如图
正方形的边
∽
∽
设,则,
在中,
即
解得
红、蓝两张纸片的面积之和
.
故选:.
3.【答案】
【解析】解:如图,中,,,
可知,
过点作,垂足为,交于.
,
.
,
,,
∽,
.
设,则有:,
解得,
故选:.
中,求出,过点作,垂足为,交于,三角形的面积公式求出的长度,由相似三角形的判定定理得出∽,设边长,根据相似三角形的对应边成比例求出的长度可得.
本题主要考查把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出边长,熟练掌握对应高的比等于相似比是关键.
4.【答案】
【解析】解:四边形是平行四边形,
,,,
点、分别是、的中点,
,,
,
,
四边形是平行四边形,
,
,
;故选项A不符合题意;
,
,
,
,
,,
,
,
四边形是平行四边形,
四边形是菱形,
,故选项B不符合题意;
延长,交延长线于,
四边形是平行四边形,
,
,
为中点,
,
在和中,
,
≌,
,,
,
,
,
,
,
故选项C不符合题意;
四边形是菱形,
,
,,
,故选项D符合题意;
故选:.
根据平行四边形的性质得到,,,根据三角形中位线的性质得到,,根据平行线的性质得到;故选项A不符合题意;根据菱形的判定定理得到四边形是菱形,根据菱形的性质得到,故选项B不符合题意;延长,交延长线于,根据全等三角形的性质得到,,求得,故选项C不符合题意;根据菱形的性质得到,推出,故选项D符合题意.
本题考查了平行四边形的性质,菱形的判定,平行线的性质,全等三角形的性质和判定,等腰三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.
5.【答案】
【解析】解:,
,
,.
,
,
,
为的平分线,
,
,
,
连接并延长交于,
,
,
是的中点,
,
在和中,
,
≌,
,,
,
是的中点,
.
故选:.
根据勾股定理得到,根据平行线的性质和角平分线的定义得到,求得,连接并延长交于,根据全等三角形的性质得到,,求得,根据三角形中位线定理即可得到结论.
此题考查了三角形的中位线定理,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
6.【答案】
【解析】解:如图,分别过点,作的垂线,垂足为,,过点作于点,
四边形是矩形,
,,
,,
,
又点和点分别是线段和的中点,
和分别是和的中位线,
,,
,,
,
,,
设,
,,
在中,,
在中,,
,
,
解得,即,
在中,.
故选:.
分别过点,作的垂线,垂足为,,过点作于点,由中位线定理及勾股定理可分别表示出线段和的长,建立等式可求出结论.
本题主要考查中位线定理,勾股定理等,构造中位线是解题过程中常见思路.
7.【答案】
【解析】
【分析】
本题考查了正方形的性质、勾股定理、锐角三角函数、等腰三角形的性质、正确作出辅助线是解决本题的关键.
由大正方形是由四个全等的直角三角形和一个小正方形组成,可得,可得,过点作于点,由三角形为等腰直角三角形可证得三角形也为等腰直角三角形,设,则,由,可解得,进而可得,即可求出
【解析】
解:由图可知,,
则,,
大正方形是由四个全等的直角三角形和一个小正方形组成,
故AE
则
则在中,有,
即
过点作于点,如图所示.
四边形为正方形,为对角线,
为等腰直角三角形,
,
故为等腰直角三角形.
设,则,
解得:.
8.【答案】
【解析】
【分析】
本题考查了矩形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、锐角三角函数、含角的直角三角形、角的计算等知识.
当点为中点时,作于点,首先利用矩形的性质和在直角三角形中若直角边等于斜边的一半知;然后利用等腰直角三角形的性质和角的和差计算即可求出,从而知结论正确;
证明即可知结论正确;
分析可知当时,点到的距离最大为值,利用等腰直角三角形性质即可知结论正确;
分析知点始终在上运动,且在由到的运动过程中,点到的距离越来越大,所以假设当点与点重合时距离最短,求出最短距离即可知结论错误.
【解答】
解:如图,当点为中点时,作于点,
由矩形中知
点为中点,,
,
在中,,,
,
,
且,
是等腰直角三角形,,
,
故结论正确;
如图,过点作于点,于点,则,
,,
,
,
由题知,
在和中,
,
,故结论正确;
是等腰直角三角形,,
,
分析可知当时,点到的距离最大,最大值为,故结论正确;
由题意可知,点始终在上运动,且在由到的运动过程中,点到的距离越来越大,所以假设当点与点重合时距离最短,如图,作,则,
由知,且,
,
点不与,重合,
点到的距离大于,故结论错误.
综上所述,结论正确.
故选C.
9.【答案】
【解析】解:观察图象可知:点在上运动的时间为,在上运动的时间为,点在上运动的时间为,
所以,,,
,
,
,故A正确,
在中,,,
,
,故B正确,
当时,点在上,,又易知此时的,
中边上的高,
,故C正确,
故选:.
由图中信息一一判断即可解决问题.
本题考查动点问题的函数图象,解题的关键是理解题意,读懂图象信息,灵活运用所学知识解决问题,是中考选择题中的压轴题.
10.【答案】
【解析】
【分析】
本题考查了翻折变换、全等三角形的判定与性质、正方形的性质,解决本题的关键是综合运用以上知识.
根据四边形是正方形,和翻折即可证明正确;
结合和翻折的性质,利用勾股定理可得,进而根据三角形内角和可得正确;
根据,的值即可判定正确;
根据
即可计算,可以判断错误;
根据已知求得,,即可判断错误.
【解答】
解:四边形是正方形,
,,
由翻折可知:
,,
,,
在和中,
≌,
所以正确;
≌,
,,
,
,
,
在中,,
,
,
根据勾股定理,得
,
即,
解得,
,
,
所以正确;
由得,,
由得≌,
,
,
是等腰三角形,
,
≌
,
,
,
,故正确,
,故正确
,,
又,
,
.
所以错误.
所以其中正确的是,一共个.
故选:.
11.【答案】
【解析】
【分析】
本题考查解直角三角形,平行线的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
如图取格点,连接,则过点作于利用面积法求出,再利用勾股定理求出即可解决问题.
【解答】
解:如图取格点,连接,则.
过点作于.
,,
,
,
,
,
,
故选A.
12.【答案】
【解析】解:在矩形中,,,,
,
,垂足为点,
,
,
∽,故正确;
,
∽,
,
为的中点,
,
,
,故正确;
过作,交于,则,
,
四边形为平行四边形,
,即为的中点,
为的中点,
,故正确;
根据已知条件无法判断,故无法得到,故错误;
设,则,
∽,
,
,
:::,
,
,
,
:::,故正确.
综上,正确个数有个.
故选:.
结合矩形的性质证明,,可证明;证明∽,利用相似三角形的性质可证明;过作,于,则,证明为的中点,可证明;根据已知条件无法证明;设,则,由相似三角形的性质可求解相关三角形的面积,进而可求得,即可证明.
本题主要考查相似三角形的判定与性质,矩形的性质,解直角三角形等知识的综合运用.
13.【答案】;
.
【解析】
【分析】
本题主要考查了等腰三角形的性质、相似三角形的性质与判定、勾股定理等,解题关键是正确作出辅助线构造直角三角形和相似三角形.
过作于,证明∽,得出,根据等腰三角形的性质和勾股定理求出、,即可进行解答;
过作于,过作于,根据等腰三角形性质结合已知条件和勾股定理分别求出和的长,再证明∽,,代入数据可计算出的长即为点上升的高度.
【解答】
解:过作于,
,
,
,
∽,
,
米,米,
米,
米,
,
米,
故答案为:;
过作于,过作于,则,
米,::,
米,
米,
米,
,
∽,
,
即,
米,
故G点上升的高度为米.
故答案为:.
14.【答案】
【解析】解:如图所示,取的中点,连接,,
,
,
又,,
,
,
是等边三角形,
,
,
,,
,,
即,,
,
中,,
故答案为:.
取的中点,连接,,依据直角三角形斜边上中线的性质,即可得到是等边三角形,进而得出,再根据三角形外角性质以及三角形内角和定理,即可得到的度数.
本题主要考查了直角三角形斜边上中线的性质,即在直角三角形中,斜边上的中线等于斜边的一半.解决问题的关键是利用三角形外角性质得到,.
15.【答案】
【解析】
【分析】
本题考查了翻折变换,勾股定理,锐角三角函数等知识,求出点落在和上时的值是本题的关键.由勾股定理可而且的长,分别求出当点落在上时和当点落在上时,的长,即可求解.
【解答】
解:,,,
,
当点落在上时,如图,
将沿折叠,点落在处,
,
,
,
当点落在上时,如图,过点作于,
将沿折叠,点落在处,
,
,
,
,
,
,
,
,,
,
当点在内部不含边界时,长度的取值范围为.
16.【答案】
【解析】解:根据题意可知:,,
在和中,
,
≌,故正确;
在正方形中,
,,
,
点在边上,
,
,
四边形是姜形,故错误;
如图,过点作于点,
,,
,
,
设,,
,,
,,
,,
,
,
,
在中,根据勾股定理得:
,
,
在中,根据勾股定理得:
,
,
,
整理得,
在中,根据勾股定理得:
,
,
整理得,
,
解得或舍去,
,
,,
,,,故正确;
,
,
的周长是,故错误;
如图,连接交于点,
垂直平分,
,
,
,
,故正确;
所以正确的结论有.
故答案为:.
根据折叠的性质可得≌即可判断正确;再根据正方形的性质可得,进而可以判断错误;过点作于点,则,,可得,设,,则,,根据勾股定理即可判断正确;再利用公股定理计算的周长是,进而可以判断错误;然后连接交于点,则垂直平分,利用勾股定理和锐角三角函数,可以判断正确.
本题主要考查了正方形的性质,图形的折叠,勾股定理,解直角三角形,熟练掌握正方形的性质,图形的折叠,勾股定理,正确作出辅助线,构造直角三角形是解题的关键.
17.【答案】解:如图,过点作于,
则四边形是矩形,
所以,米,
米,
由题意得,,
所以,米,
树高米.
【解析】过点作于,根据同时同地物高与影长成正比列比例式求出的长度,再根据矩形的对边相等可得,然后根据计算即可得解.
本题考查了相似三角形的应用,熟记同时同地物高与影长成正比并列出比例式是解题的关键,难点在于作辅助线构造出三角形.
18.【答案】解:根据题意得出:,
则∽,
故,
,,,
,
解得:,
河的宽度为米.
【解析】根据相似三角形的性质得出,进而代入求出即可.
此题主要考查了相似三角形的判定与性质,根据已知得出∽是解题关键.
19.【答案】解:;
如图:设为乙树的高度,米,
四边形是平行四边形,
米
由题意得:,
解得:米,
故乙树的高度米;
;
如图:设为丁树的高度,米,米,
四边形是平行四边形,
,
由题意得:,解得:米,
,解得米,
故AE米,
故丁树的高度米.
【解析】
【分析】
本题考查了相似三角形的应用,解题的关键是从复杂的数学问题中整理出三角形并利用相似三角形求解,考查了同学们的建模能力.
直接利用同一时刻物体的影长与实际高度比值不,变进而得出答案;
直接利用平行四边形的性质得出的长,进而得出答案;
首先画出基本图形,进而分别求出,的长,即可得出答案;
首先画出基本图形,进而分别求出,的长,即可得出答案.
【解答】
解:一根长为米的竹竿的影长为米,甲树的影长为米,
甲树的高度为:米.
故答案为:;
见答案;
如图,
设为丙树的高度,米,由题意得:,米,
则米,
四边形是平行四边形,
米,
又由题意得,
米,
米,
故选:.
见答案.
20.【答案】解:;
如图,过点作,
,
,即,
又,
,
,
,,
,
,
;
如图,过点作,
平分,平分,
,,
由可得,
,
设,,则
,,,,
,
,,
,
中,由,可得
,整理得:,
由,可得
,整理得:,
由解得,
,
.
【解析】
【分析】
本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角补角相等进行推导.余角和补角计算的应用常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.
根据平行线的性质以及直角三角形的性质进行证明即可;
先过点作,根据同角的余角相等,得出,再根据平行线的性质,得出,即可得到;
先过点作,根据角平分线的定义,得出,再设,,根据,可得,根据,可得,最后解方程组即可得到,进而得出.
【解答】
解:如图,,
,
,
,
,
故答案为:;
见答案;
见答案.
21.【答案】证明:平行四边形,
,,
为中点,
,
,,
四边形为平行四边形,
又,
,
,
故四边形为菱形;
在中,,,
,
为中点,也为的中点,
,
四边形的面积;
应添加条件.
证明:,为中点,
三线合一的性质,即.
四边形为平行四边形,四边形为平行四边形,
,.
四边形为正方形.对角线互相垂直且相等的四边形是正方形
【解析】由题意容易证明平行且等于,又知,所以得到四边形为菱形;
根据解三角形的知识求出和的长,然后根据菱形的面积公式求出四边形的面积;
应添加条件,证明且相等即可.
本题主要考查正方形的判定、菱形的判定与性质和勾股定理等知识点,此题是道综合体,有一定的难度,解答的关键还是要能熟练掌握各种四边形的基本性质.
22.【答案】解:
;
的度数不变.
平分,平分
,
又
.
过作,
又
,
存在原因如下:
当点在直线上时如图,
当点在直线上时如图,
点在直线,之间不含在,上
,
,
若,
则
,,为正整数
解得
,,或
当时,
当时,,不合题意,舍去
当时,
当时,.
综上所述,存在正整数,,,满足题意.
【解析】此题考查了平行线的性质,角的平分线,一元一次不等式组的应用,角的计算等.
根据平行线的性质,可得到,再根据,再根据代入可得到的度数;
根据角的平分线定义,平行线的性质可得到,再根据对顶角定义得到,进而得到,再使用平行线的性质即可得到的度数;
可分情况:当点在直线上时如图,;当点在直线上时如图,,列出相应的一元一次不等式组,再分别求得对应的和的值,根据实际进行讨论取合适的值.
23.【答案】解:,,
,,
是的中点,
,
在反比例函数图象上,
,
反比例函数的解析式为,
点的纵坐标为,
;
点的横坐标为,
,
,
的纵坐标为,
,
,
在中,,
如图,由知,,
,,
过点作于,
,,
,
由折叠知,,,,
,
,
,
∽,
,
,
,
在中,,
,
,
反比例函数解析式为.
【解析】此题是反比例函数综合题,主要考查了待定系数法,中点坐标公式,相似三角形的判定和性质,锐角三角函数,求出:是解本题的关键.
先确定出点坐标,进而得出点坐标,即可得出结论;
先确定出点的横坐标,进而表示出点的坐标,得出,同理表示出,即可得出结论;
先判断出∽,即可求出,最后用勾股定理求出,即可得出结论.
24.【答案】解:,,
令可得:,
解得:,,
点在点的左侧,
点的坐标为,点的坐标为;
由可知,且为抛物线的顶点,如图,过点作,则.
当为等腰直角三角形时,,,
点的坐标为,
,
点的坐标为.
将点代入中,得,
抛物线表达式为.
当时,则有,设点的坐标为,
过点作轴的垂线,进而有,
当时,即,
,
此方程无解;
当时,即,
,
,
解得,,
将时,;
将时,.
综上所述,点的坐标为或
【解析】本题主要考查了二次函数与等腰直角三角形、锐角三角函数的综合,熟练掌握二次函数的图象与性质以及等腰直角三角形的性质是解决本题的关键.
先将二次函数一般式化为交点式,再令得出关于的一元二次方程并求解,最后根据、的位置即可确定坐标;
先求出的长,再作出图象并过点作,根据直角三角形斜边上的中线等于斜边的一半可知,再根据等腰直角三角形的性质结合锐角三角函数的定义与可分别求得点、的坐标,从而利用待定系数法可确定二次函数解析式,进而设点的坐标为,过点作轴的垂线,根据锐角三角函数的定义与可得关于的含绝对值的方程,最后分类讨论解此含绝对值的方程即可解决问题.
25.【答案】解:如图,当边恰好经过点时,
是等边三角形,
,
,
在中,
,,
,
解得,即,
,
当边恰好经过点时,;
如图,过点作于,
当时,
,
,
,,
,
;
如图,当时,
,,
,
四边形是矩形,
,
∽,
,
,
,,,
;
如图,当时,
,,
,
,
,
;
当时,
,
高为:,
;
存在.
在中,,
,
,
,
或,
如图,当时,
过点作与,
则,
在中,
,即,
,
即或;
或;
如图,当时,,
,
,,
,
,即或,
或;
如图,当时,
,
,
点和点重合,
,
当刚开始时,,
当返回时,
,舍去,
综上所述当,,,,时,是等腰三角形.
【解析】此题是四边形的综合题目,主要涉及知识点矩形的性质和判定以及解直角三角形的知识和等腰三角形的判定.
当边恰好经过点时,由得,在中,根据三角函数求得的值;
根据运动的时间为不同的取值范围,求等边和矩形重叠部分的面积为的值,当时,重叠部分是直角梯形,面积等于梯形的面积,
当时,重叠部分是,当时,重叠部分是,当时,重叠部分是正三角形的面积;
当时,,在中,由即,得,即或,求出或;
当时,,又因为得到,再由,求出,即或,求出或;
当时,所以,得到点和点重合,从而求出的值.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
