12.1 全等三角形 课件(共27页)
图片预览



文档简介
(共27张PPT)
12.1 全等三角形
精品同步教学课件
观看下面图形,试着构建全等形定义.
定义:能够完全重合的两个图形.
全等形的定义及性质
性质:形状和大小一定都相等
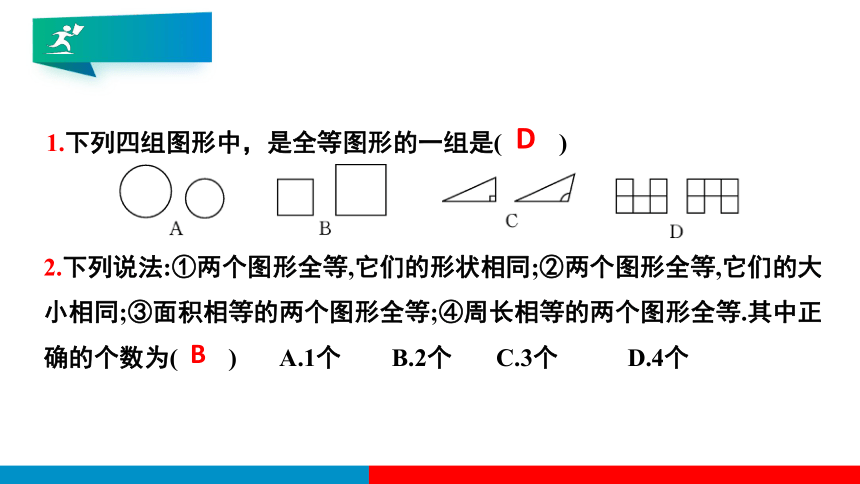
1.下列四组图形中,是全等图形的一组是( )
2.下列说法:①两个图形全等,它们的形状相同;②两个图形全等,它们的大小相同;③面积相等的两个图形全等;④周长相等的两个图形全等.其中正确的个数为( ) A.1个 B.2个 C.3个 D.4个
D
B
全等三角形的概念
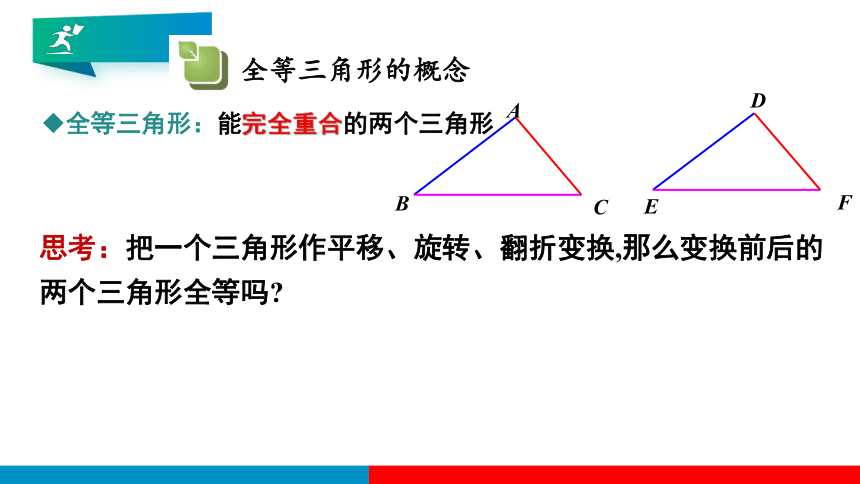
全等三角形:能完全重合的两个三角形
A
B
C
E
D
F
思考:把一个三角形作平移、旋转、翻折变换,那么变换前后的两个三角形全等吗
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
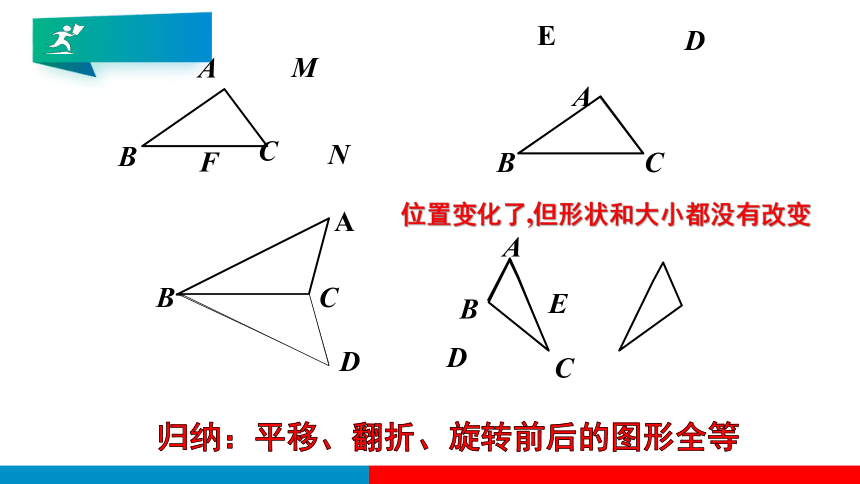
归纳:平移、翻折、旋转前后的图形全等
位置变化了,但形状和大小都没有改变
全等三角形的对应元素
A
B
C
E
D
F
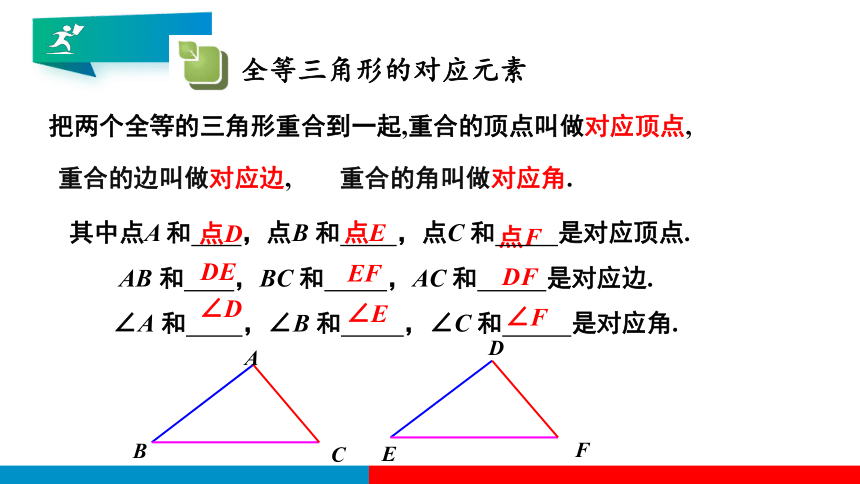
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
其中点A 和 ,点B 和 ,点C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
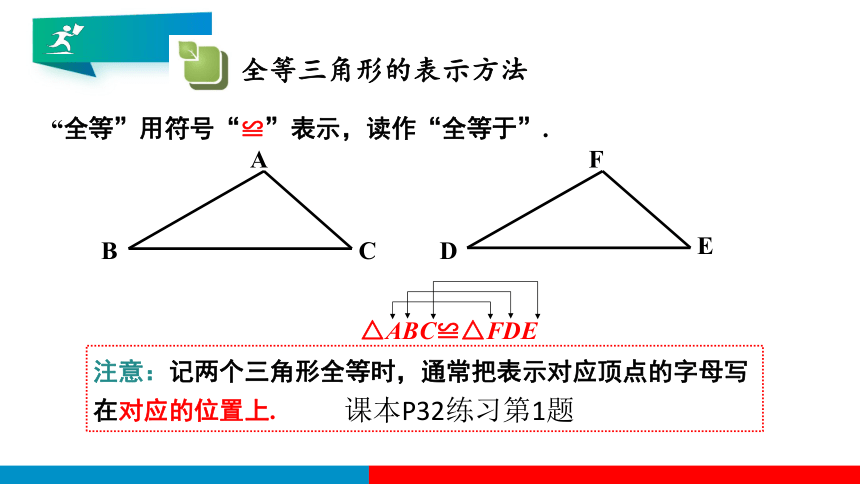
全等三角形的表示方法
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
“全等”用符号“≌”表示,读作“全等于”.
课本P32练习第1题
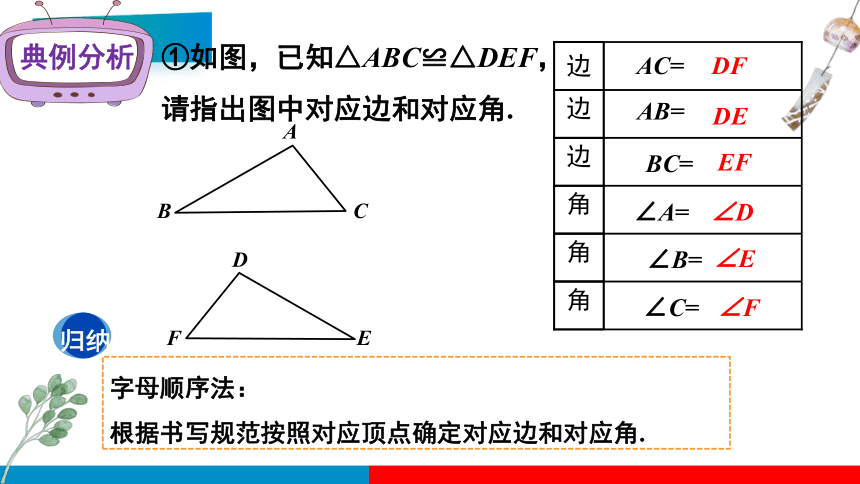
典例分析
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC=
AB=
BC=
∠A=
∠B=
∠C=
①如图,已知△ABC≌△DEF,请指出图中对应边和对应角.
A
B
C
F
D
E
字母顺序法:
根据书写规范按照对应顶点确定对应边和对应角.
归纳
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC=
AB=
BC=
∠A=
∠B=
∠C=
变式:如图,已知△ABC和△DEF是全等三角形,请指出图中对应边和对应角.
A
B
C
F
D
E
(2)图形特征法:① 长边对长边,短边对短边.
②大角对大角,小角对小角.
归纳
典例分析
角
角
角
边
边
边
AB=
AC=
BC=
∠BAC=
∠B=
∠C=
AD
AE
DE
∠DAE
∠D
∠E
如图,请指出图中两个全等三角形的对应边和对应角.
A
B
C
D
E
∠1= ∠2
2
1
对顶角相等,一定为一对对应角.
归纳
总结归纳
全等三角形对应元素的确定方法
(2)图形特征法:
① 长边对最长边,短边对短边.
②大角对最大角,小角对最小角.
③等边对等边,等角对等角
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
全等三角形对应元素的确定方法
(1)字母顺序法:
根据书写规范按照对应顶点确定元素
(2)图形特征法:
① 长边对长边,短边对短边.
②大角对大角,小角对小角.
③等边对等边,等角对等角
(3)动态变换法:
将图形进行动态变换后重合确定对应元素
两个全等三角形,对应边有什么关系 对应角呢
全等三角形的性质
性质:全等三角形的对应边相等,全等三角形的对应角相等.
A
B
C
E
D
F
几何语言:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF(全等三角形的对应边相等)
∠A =∠D,∠B =∠E,∠C =∠F(全等三角形的对应角相等).
答:其他对应边: AC 和 CA;
对应角:∠B 和∠D,∠ACB 和∠CAD,∠CAB 和∠ACD.
(教材第1题)如图,△ABC≌△CDA,AB和CD,BC和DA是
对应边.写出其他对应边及对应角.
解:(1) 对应边:FG 和 MH,EF 和 NM,EG 和 NH;其他对应角:∠E 和∠N,∠EGF 和∠NHM.
(2) NM = EF = 2.1 cm,EG = NH = 3.3 cm.
∴ HG = EG – EH = 3.3 – 1.1 = 2.2 (cm).
2.(教材第4题)如图,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边,EF=2.1 cm,EH=1.1 cm,NH=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段NM及线段HG的长度.
∠ADE
∠E
∠A
ED
AD
AE
A
B
C
E
D
角
角
角
边
边
边
AB=
AC=
BC=
∠A=
∠B=
∠ACB=
3.如图,已知△ABC和△ADE是全等三角形,请指出图中对应边和对应角.
A
B
C
E
D
如图,已知△ABC≌△AED,若AB=6,AC=2,∠B=25°,你还能说出△ADE中其他角的大小和边的长度吗
你能算出BD的长吗?
解:∵△ABC≌△AED,
∴∠E=∠B=25°(全等三角形对应角相等),
AD=AC=2,AE=AB=6(全等三角形对应边相等).
变式:
解:根据全等三角形的对应角相等,由图可知∠1 = 180° – 60° – 54° = 66°.
4. (教材第3题)如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度
解:相等.理由如下:
∵△ABC ≌ △DEC,
∴∠ACB =∠DCE(全等三角形的对应角相等).
∴∠ACB – ∠ACE =∠DCE – ∠ACE(等式的基本性质),
即∠BCE =∠ ACD .
5. (教材第5题)如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,∠ACD和∠BCE相等吗 为什么
解:(1) 对应边:AB 和 AC,AD 和 AE,BD 和 CE.
对应角:∠A 和 ∠A,∠ABD 和 ∠ACE,∠ADB 和 ∠AEC.
6. (教材第6题)如图,△AEC≌△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
解:(2)∵△AEC ≌ △ADB,
∴∠ACE = ∠ABD = 39°.
在△ABC 中,∠A +∠ABC +∠ACB = 180°,即∠A +∠ABD +∠1 +∠2 +∠ACE = 180°.
又∵∠1=∠2,
∴ 50° + 39° + 2∠1 + 39° = 180°,解得∠1 = 26°.
6.如图,△AEC≌△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
常见全等三角形展示
https://www.21cnjy.com/help/help_extract.php
12.1 全等三角形
精品同步教学课件
观看下面图形,试着构建全等形定义.
定义:能够完全重合的两个图形.
全等形的定义及性质
性质:形状和大小一定都相等
1.下列四组图形中,是全等图形的一组是( )
2.下列说法:①两个图形全等,它们的形状相同;②两个图形全等,它们的大小相同;③面积相等的两个图形全等;④周长相等的两个图形全等.其中正确的个数为( ) A.1个 B.2个 C.3个 D.4个
D
B
全等三角形的概念
全等三角形:能完全重合的两个三角形
A
B
C
E
D
F
思考:把一个三角形作平移、旋转、翻折变换,那么变换前后的两个三角形全等吗
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
归纳:平移、翻折、旋转前后的图形全等
位置变化了,但形状和大小都没有改变
全等三角形的对应元素
A
B
C
E
D
F
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
其中点A 和 ,点B 和 ,点C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
全等三角形的表示方法
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
“全等”用符号“≌”表示,读作“全等于”.
课本P32练习第1题
典例分析
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC=
AB=
BC=
∠A=
∠B=
∠C=
①如图,已知△ABC≌△DEF,请指出图中对应边和对应角.
A
B
C
F
D
E
字母顺序法:
根据书写规范按照对应顶点确定对应边和对应角.
归纳
DF
DE
EF
∠D
∠E
∠F
角
角
角
边
边
边
AC=
AB=
BC=
∠A=
∠B=
∠C=
变式:如图,已知△ABC和△DEF是全等三角形,请指出图中对应边和对应角.
A
B
C
F
D
E
(2)图形特征法:① 长边对长边,短边对短边.
②大角对大角,小角对小角.
归纳
典例分析
角
角
角
边
边
边
AB=
AC=
BC=
∠BAC=
∠B=
∠C=
AD
AE
DE
∠DAE
∠D
∠E
如图,请指出图中两个全等三角形的对应边和对应角.
A
B
C
D
E
∠1= ∠2
2
1
对顶角相等,一定为一对对应角.
归纳
总结归纳
全等三角形对应元素的确定方法
(2)图形特征法:
① 长边对最长边,短边对短边.
②大角对最大角,小角对最小角.
③等边对等边,等角对等角
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
全等三角形对应元素的确定方法
(1)字母顺序法:
根据书写规范按照对应顶点确定元素
(2)图形特征法:
① 长边对长边,短边对短边.
②大角对大角,小角对小角.
③等边对等边,等角对等角
(3)动态变换法:
将图形进行动态变换后重合确定对应元素
两个全等三角形,对应边有什么关系 对应角呢
全等三角形的性质
性质:全等三角形的对应边相等,全等三角形的对应角相等.
A
B
C
E
D
F
几何语言:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF(全等三角形的对应边相等)
∠A =∠D,∠B =∠E,∠C =∠F(全等三角形的对应角相等).
答:其他对应边: AC 和 CA;
对应角:∠B 和∠D,∠ACB 和∠CAD,∠CAB 和∠ACD.
(教材第1题)如图,△ABC≌△CDA,AB和CD,BC和DA是
对应边.写出其他对应边及对应角.
解:(1) 对应边:FG 和 MH,EF 和 NM,EG 和 NH;其他对应角:∠E 和∠N,∠EGF 和∠NHM.
(2) NM = EF = 2.1 cm,EG = NH = 3.3 cm.
∴ HG = EG – EH = 3.3 – 1.1 = 2.2 (cm).
2.(教材第4题)如图,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边,EF=2.1 cm,EH=1.1 cm,NH=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段NM及线段HG的长度.
∠ADE
∠E
∠A
ED
AD
AE
A
B
C
E
D
角
角
角
边
边
边
AB=
AC=
BC=
∠A=
∠B=
∠ACB=
3.如图,已知△ABC和△ADE是全等三角形,请指出图中对应边和对应角.
A
B
C
E
D
如图,已知△ABC≌△AED,若AB=6,AC=2,∠B=25°,你还能说出△ADE中其他角的大小和边的长度吗
你能算出BD的长吗?
解:∵△ABC≌△AED,
∴∠E=∠B=25°(全等三角形对应角相等),
AD=AC=2,AE=AB=6(全等三角形对应边相等).
变式:
解:根据全等三角形的对应角相等,由图可知∠1 = 180° – 60° – 54° = 66°.
4. (教材第3题)如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度
解:相等.理由如下:
∵△ABC ≌ △DEC,
∴∠ACB =∠DCE(全等三角形的对应角相等).
∴∠ACB – ∠ACE =∠DCE – ∠ACE(等式的基本性质),
即∠BCE =∠ ACD .
5. (教材第5题)如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,∠ACD和∠BCE相等吗 为什么
解:(1) 对应边:AB 和 AC,AD 和 AE,BD 和 CE.
对应角:∠A 和 ∠A,∠ABD 和 ∠ACE,∠ADB 和 ∠AEC.
6. (教材第6题)如图,△AEC≌△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
解:(2)∵△AEC ≌ △ADB,
∴∠ACE = ∠ABD = 39°.
在△ABC 中,∠A +∠ABC +∠ACB = 180°,即∠A +∠ABD +∠1 +∠2 +∠ACE = 180°.
又∵∠1=∠2,
∴ 50° + 39° + 2∠1 + 39° = 180°,解得∠1 = 26°.
6.如图,△AEC≌△ADB,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,且∠1=∠2,求∠1的度数.
常见全等三角形展示
https://www.21cnjy.com/help/help_extract.php
