12.2 第3课时 “角边角”“角角边” 课件(共21页)
文档属性
| 名称 | 12.2 第3课时 “角边角”“角角边” 课件(共21页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 09:39:02 | ||
图片预览


文档简介
(共21张PPT)
12.2三角形全等的判定
精品同步教学课件
第3课时 “角边角”“角角边”
如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
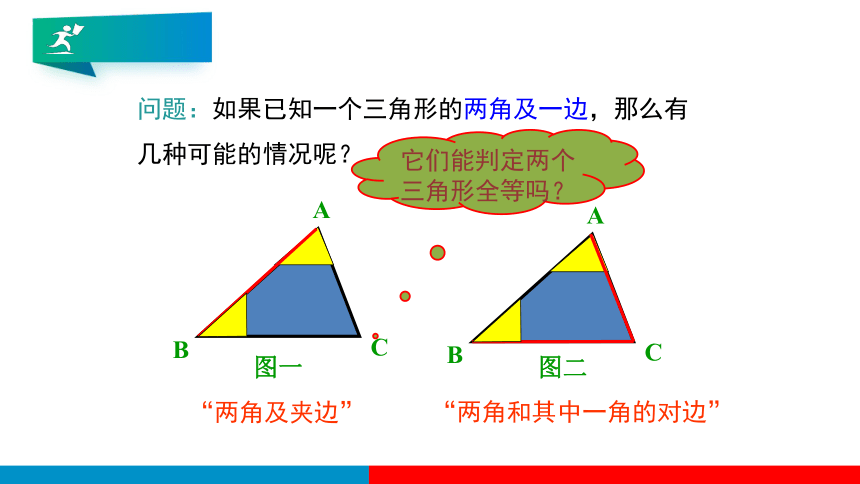
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
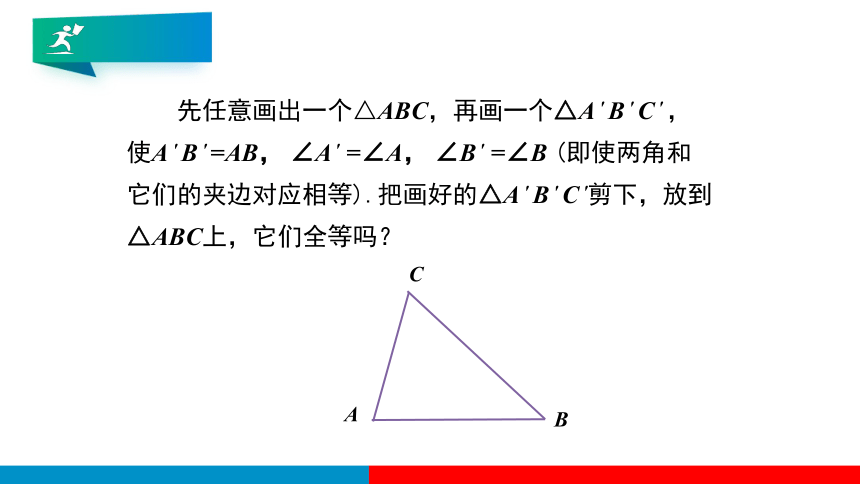
先任意画出一个△ABC,再画一个△A ′ B ′ C ′ , 使A ′ B ′ =AB, ∠A ′ =∠A, ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下,放到△ABC上,它们全等吗?
A
C
B
A
C
B
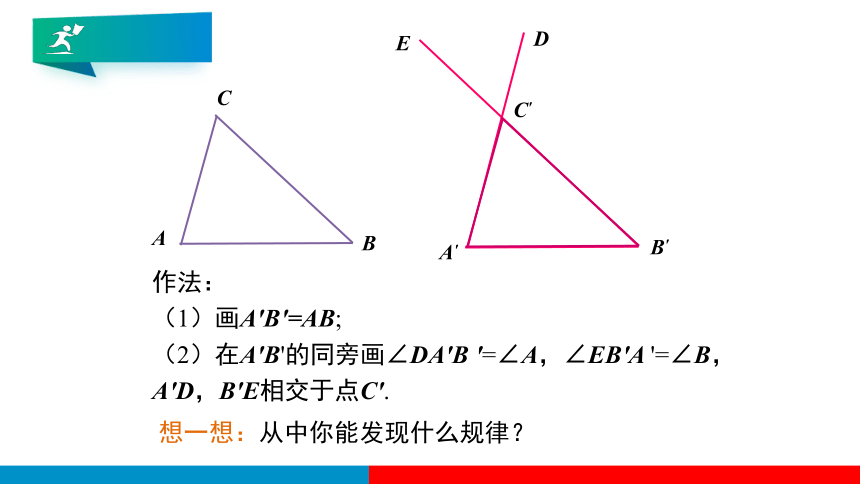
A′
B′
C′
E
D
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A '=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
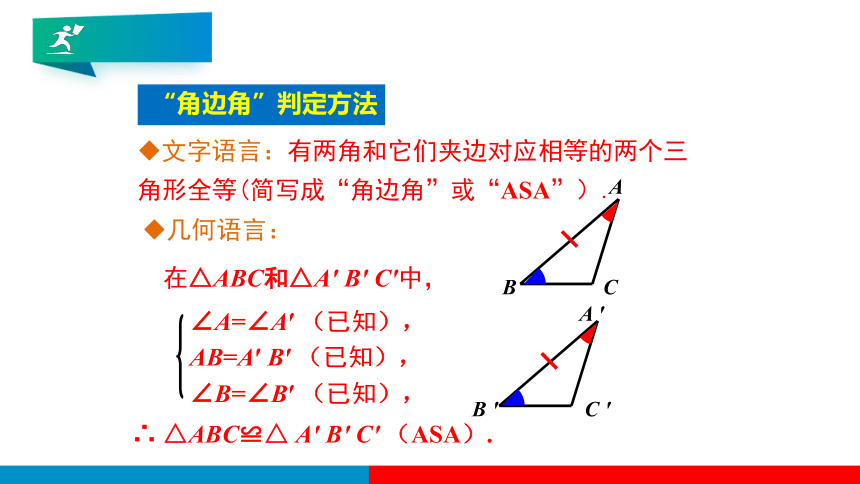
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
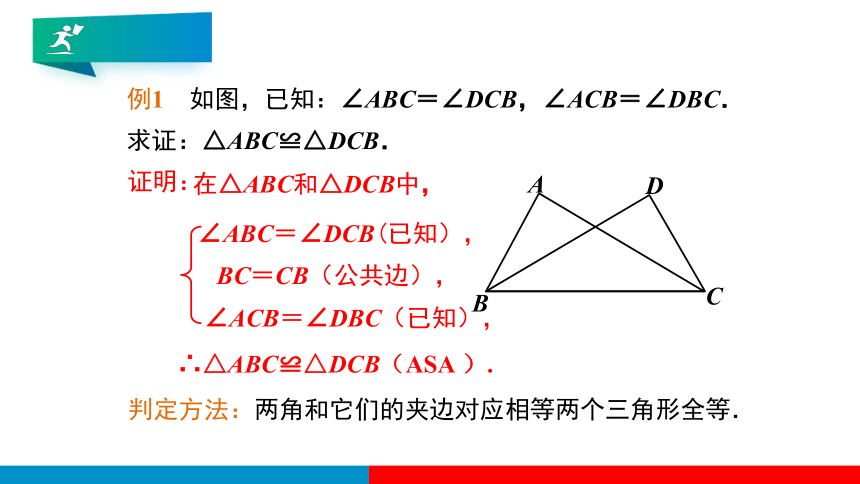
例1 如图,已知:∠ABC=∠DCB,∠ACB=∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
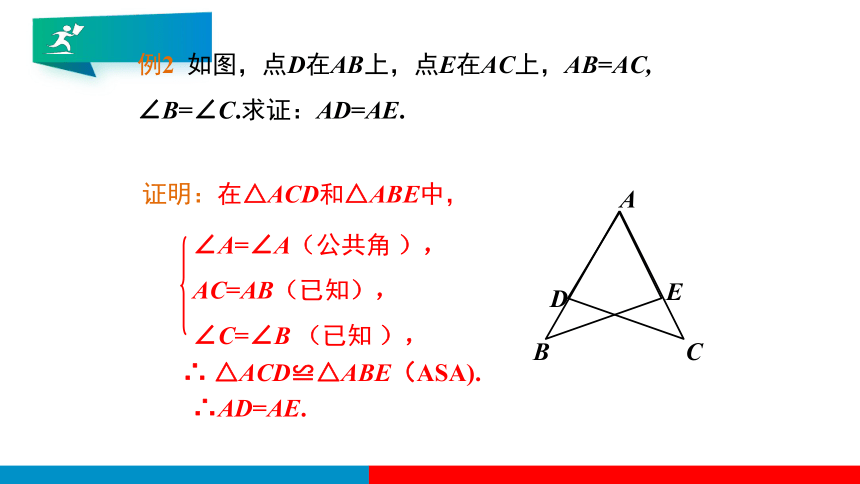
例2 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
A
B
C
D
E
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA).
∴AD=AE.
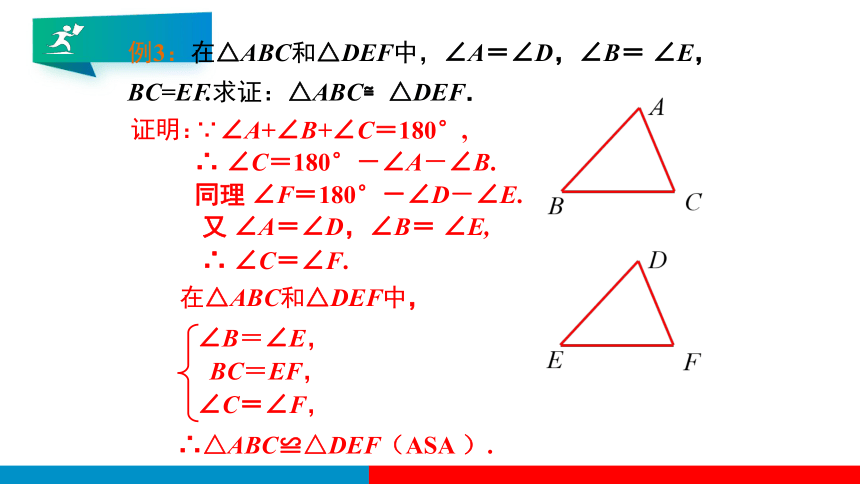
例3:在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
证明:
∵∠A+∠B+∠C=180°,
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC和△DEF中,
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
归纳总结
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:带1去,因为有两角且夹边相等的两个三角形全等.
如图12.2-10,已知AB=AC,AD=AE,求证△ BOD ≌△ COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
例4
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(SAS). ∴∠ B= ∠ C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(AAS).
练习.[中考·玉林] 如图,AB=AE, ∠ 1= ∠ 2,∠ C = ∠ D . 求证△ ABC ≌△ AED.
教材练习1:已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
1. △ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF ,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF
C.∠A=∠D D.∠C=∠F
2. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
当堂练习
A
B
A
B
C
D
E
F
3.如图,∠ACB=∠DFE,BC=EF,那么应补充一个条件: ,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
或∠A=∠D
或 AC=DF
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
课堂小结
边角边
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”“角边角”中两角与边的区别
https://www.21cnjy.com/help/help_extract.php
12.2三角形全等的判定
精品同步教学课件
第3课时 “角边角”“角角边”
如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
先任意画出一个△ABC,再画一个△A ′ B ′ C ′ , 使A ′ B ′ =AB, ∠A ′ =∠A, ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下,放到△ABC上,它们全等吗?
A
C
B
A
C
B
A′
B′
C′
E
D
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A '=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
例1 如图,已知:∠ABC=∠DCB,∠ACB=∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
例2 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
A
B
C
D
E
证明:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA).
∴AD=AE.
例3:在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F,
证明:
∵∠A+∠B+∠C=180°,
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC和△DEF中,
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
归纳总结
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
∴ △ABC≌△ A′ B′ C′ (AAS).
A
B
C
A ′
B ′
C ′
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:带1去,因为有两角且夹边相等的两个三角形全等.
如图12.2-10,已知AB=AC,AD=AE,求证△ BOD ≌△ COE.
解题秘方:找出两个三角形中两个角及其中一角的对边对应相等,利用“AAS”判定两个三角形全等.
例4
证明:在△ ABE 和△ ACD 中,
∴△ ABE ≌△ ACD(SAS). ∴∠ B= ∠ C.
∵ AB=AC,AD=AE,∴ BD=CE.
在△ BOD 和△ COE 中,
∴△ BOD ≌△ COE(AAS).
练习.[中考·玉林] 如图,AB=AE, ∠ 1= ∠ 2,∠ C = ∠ D . 求证△ ABC ≌△ AED.
教材练习1:已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
1. △ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF ,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF
C.∠A=∠D D.∠C=∠F
2. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69° ,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
当堂练习
A
B
A
B
C
D
E
F
3.如图,∠ACB=∠DFE,BC=EF,那么应补充一个条件: ,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
或∠A=∠D
或 AC=DF
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
课堂小结
边角边
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”“角边角”中两角与边的区别
https://www.21cnjy.com/help/help_extract.php
