数学人教A版2019必修第一册5.4 三角数的图象与性质(共56张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册5.4 三角数的图象与性质(共56张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 00:00:00 | ||
图片预览






文档简介
(共56张PPT)
第五章 《三角函数》
5.4.1正弦函数、余弦函数的图象
将角的弧度视为自变量x,角的三角函数值为y,则函数y=sin x叫做正弦函数,
函数y=cos x叫做余弦函数,
二者的定义域均为R。
正弦函数、余弦函数的定义
单位圆上任意一点在圆周上旋转一周就回到原来的位置:
自变量每增加(减少)2π,正/余弦函数值将重复出现.
弧
度
角
唯一确定
正
弦
值
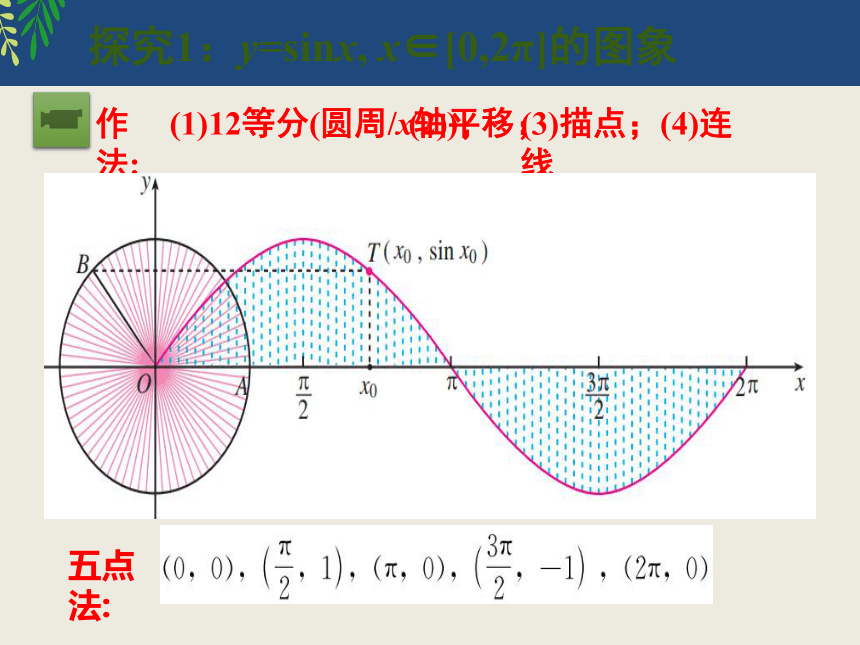
探究1:y=sinx, x∈[0,2π]的图象
作法:
(1)12等分(圆周/x轴);
(2)平移;
(3)描点;(4)连线
五点法:
正弦曲线
sin(x+k·2 )=sinx,k Z
图象左、右依次平移2π个单位长度
探究2:y=sinx, x∈R的图象
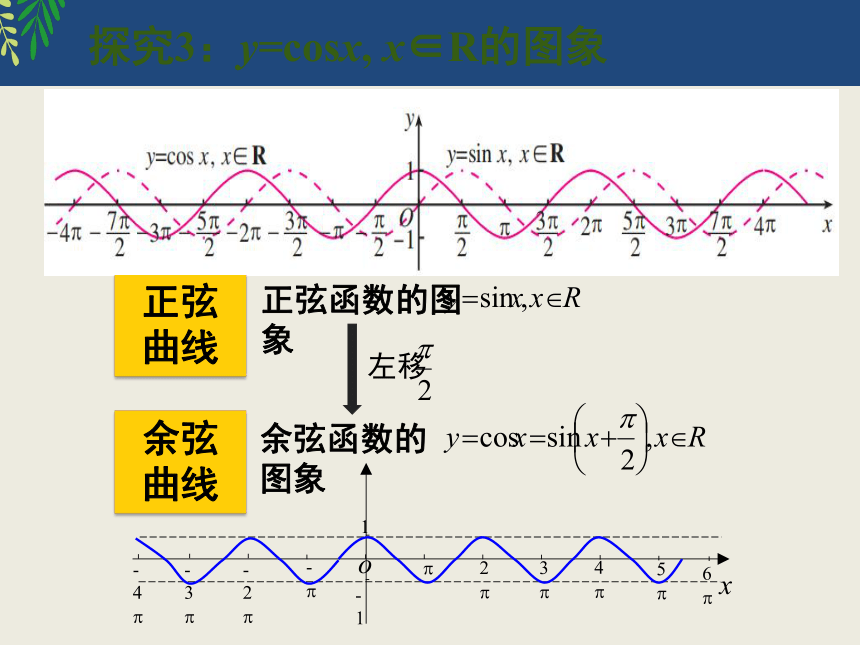
探究3:y=cosx, x∈R的图象
余弦函数的图象
正弦函数的图象
正弦曲线
余弦曲线
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
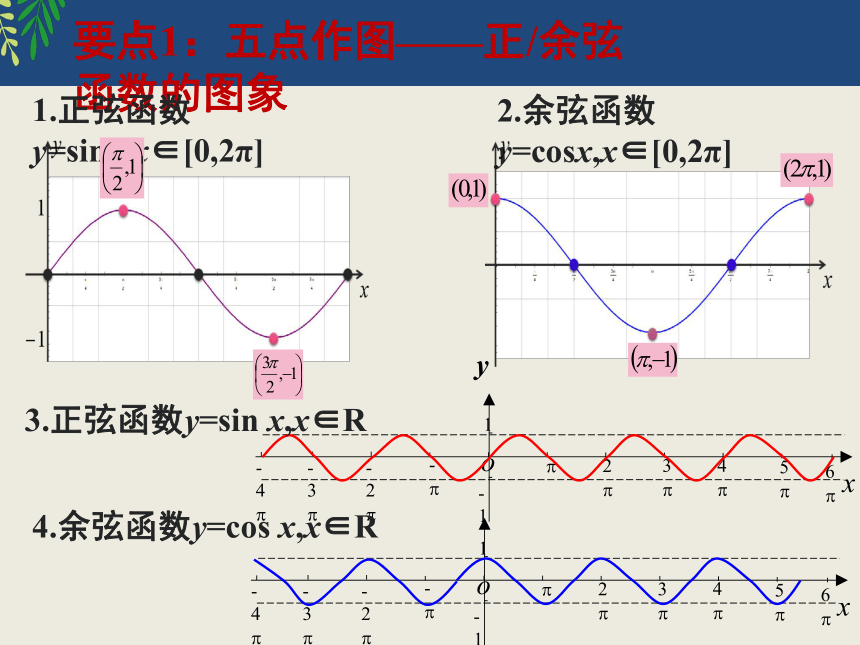
要点1:五点作图——正/余弦函数的图象
1.正弦函数y=sinx,x∈[0,2π]
2.余弦函数y=cosx,x∈[0,2π]
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
3.正弦函数y=sin x,x∈R
4.余弦函数y=cos x,x∈R
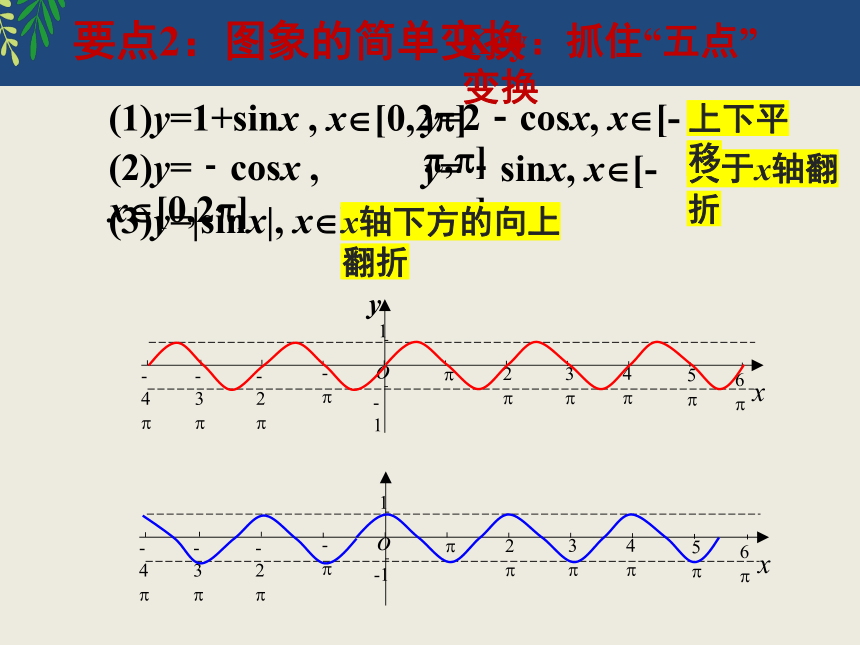
要点2:图象的简单变换
(1)y=1+sinx , x [0,2 ]
(2)y=﹣cosx , x [0,2 ]
y=﹣sinx, x [-π, ]
y=2-cosx, x [-π, ]
(3)y=|sinx|, x R
上下平移
关于x轴翻折
x轴下方的向上翻折
上下平移
x轴下方的向上翻折
Key:抓住“五点”变换
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
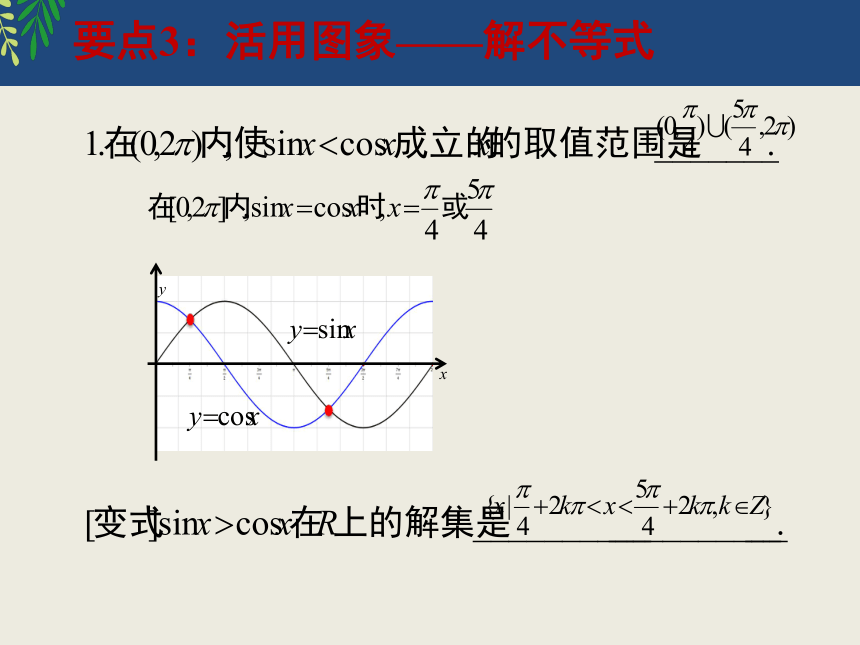
要点3:活用图象——解不等式
要点3:活用图象——解不等式
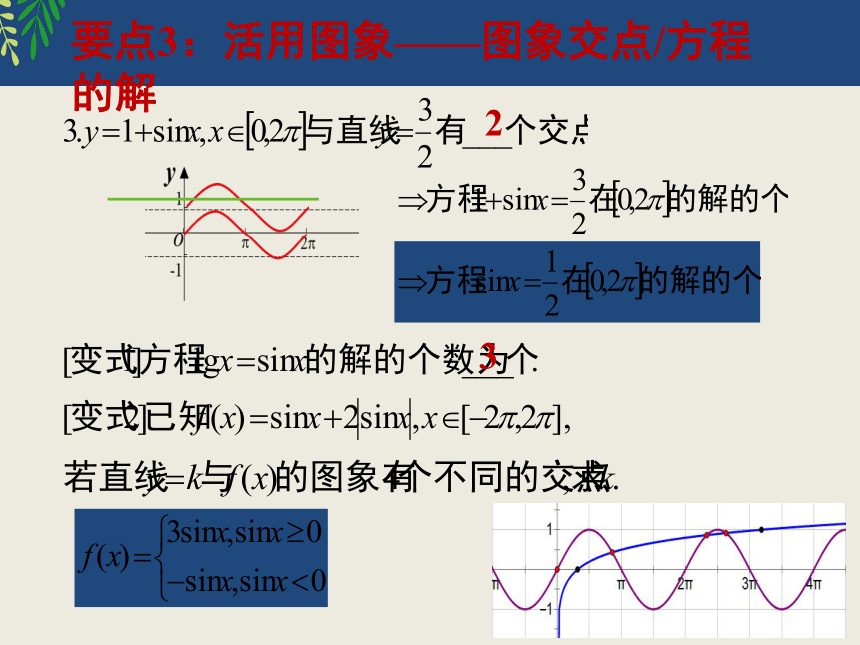
要点3:活用图象——图象交点/方程的解
2
3
第五章 《三角函数》
5.4.2正弦函数、余弦函数的性质
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cos x,x∈R
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sin x,x∈R
正弦曲线
余弦曲线
正/余弦函数值具有“周而复始”的变化规律;
周期性
1.周期性
(1)周期函数:设函数f(x)的定义域为D,若存在一个非零
常数T, 使得对每个x∈D时都有x+T∈D,且f (x+T )=f (x),
则函数f(x)叫周期函数;非零常数T叫做这个函数的周期.
思考1:根据上述定义,说说正弦函数f(x)=sinx的周期是什么
1.周期性
(1)周期函数:设函数f(x)的定义域为D,若存在一个非零
常数T, 使得对每个x∈D时都有x+T∈D,且f (x+T )=f (x),
则函数f(x)叫周期函数;非零常数T叫做这个函数的周期.
①周期函数的周期不唯一.
②若f(x)的所有周期中存在一个最小正数,
则该最小正数叫f(x)的最小正周期.
求三角函数的周期——定义法
三角函数的周期——公式法
求三角函数的周期——公式法、图象法
图象法
利用函数周期求值
Key:利用周期定义将数化到已知区间
抽象函数的周期
抽象函数的周期
2
抽象函数的周期
2.奇偶性
奇函数
偶函数
奇函数
奇函数
3.单调性
3.单调性
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
复合函数的单调性:
若原函数y=f[g(x)]由内层函数t=g(x)和外层函数y=f(t)复合而成.
则原函数的单调性满足“同增异减”原则.
内外层在I上单调性同,则原函数在I上增;
内外层在I上单调性不同,则原函数在I上减.
复合函数的单调性:
“同增异减”原则
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
“同增异减”
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
是由y=cosx左移π/3
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
求完整增区间I
赋k,求I与[-2π,2π]的交集
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
求完整减区间I
赋k,求I与[0,π]的交集
3.单调性——比较大小
用诱导公式把角化正&化小,化到同一单调区间内
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
4.最值
三角函数在对称轴取得最大或最小值
4.最值——①求R上的值域
4.最值——②求指定区间上的值域(整体法)
y=sint的图象
4.最值——②求指定区间上的值域(换元法)
换元
习题课
求三角函数的对称轴或对称中心
基础知识:①y=sinx的对称轴为
对称中心为
②y=cosx的对称轴为
对称中心为
③y=tanx的对称中心为
正余弦函数在对称轴处取得最值
求三角函数的对称轴或对称中心
基础知识:①y=sinx的对称轴为
对称中心为
②y=cosx的对称轴为
对称中心为
③y=tanx的对称中心为
正余弦函数在对称轴处取得最值
求x得对称轴
求x得对称中心
求x得对称中心
[注]对称轴应写为“x=… , k∈Z”,对称中心应写为“(… , 0),k∈Z”
求三角函数的对称轴或对称中心
三角函数的对称性与奇偶性
三角函数的单调性
三角函数的单调性
第五章 《三角函数》
5.4.3正切函数的性质与图象
正切函数y=tanx的性质
1.定义域:
3.周期性:
2.奇偶性:
奇函数
4.图象:
正切函数y=tanx的图象
正切函数y=tanx的性质
x
y
1
-1
4.图象:
5.单调性:
无最值
正切函数y=tanx的性质
4.图象:
5.单调性:
6.对称中心:
无最值
运用:解不等式
运用:正切函数的性质
运用:正切函数的性质
运用:正切函数的性质
FIGHTING
第五章 《三角函数》
5.4.1正弦函数、余弦函数的图象
将角的弧度视为自变量x,角的三角函数值为y,则函数y=sin x叫做正弦函数,
函数y=cos x叫做余弦函数,
二者的定义域均为R。
正弦函数、余弦函数的定义
单位圆上任意一点在圆周上旋转一周就回到原来的位置:
自变量每增加(减少)2π,正/余弦函数值将重复出现.
弧
度
角
唯一确定
正
弦
值
探究1:y=sinx, x∈[0,2π]的图象
作法:
(1)12等分(圆周/x轴);
(2)平移;
(3)描点;(4)连线
五点法:
正弦曲线
sin(x+k·2 )=sinx,k Z
图象左、右依次平移2π个单位长度
探究2:y=sinx, x∈R的图象
探究3:y=cosx, x∈R的图象
余弦函数的图象
正弦函数的图象
正弦曲线
余弦曲线
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
要点1:五点作图——正/余弦函数的图象
1.正弦函数y=sinx,x∈[0,2π]
2.余弦函数y=cosx,x∈[0,2π]
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
3.正弦函数y=sin x,x∈R
4.余弦函数y=cos x,x∈R
要点2:图象的简单变换
(1)y=1+sinx , x [0,2 ]
(2)y=﹣cosx , x [0,2 ]
y=﹣sinx, x [-π, ]
y=2-cosx, x [-π, ]
(3)y=|sinx|, x R
上下平移
关于x轴翻折
x轴下方的向上翻折
上下平移
x轴下方的向上翻折
Key:抓住“五点”变换
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
要点3:活用图象——解不等式
要点3:活用图象——解不等式
要点3:活用图象——图象交点/方程的解
2
3
第五章 《三角函数》
5.4.2正弦函数、余弦函数的性质
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cos x,x∈R
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sin x,x∈R
正弦曲线
余弦曲线
正/余弦函数值具有“周而复始”的变化规律;
周期性
1.周期性
(1)周期函数:设函数f(x)的定义域为D,若存在一个非零
常数T, 使得对每个x∈D时都有x+T∈D,且f (x+T )=f (x),
则函数f(x)叫周期函数;非零常数T叫做这个函数的周期.
思考1:根据上述定义,说说正弦函数f(x)=sinx的周期是什么
1.周期性
(1)周期函数:设函数f(x)的定义域为D,若存在一个非零
常数T, 使得对每个x∈D时都有x+T∈D,且f (x+T )=f (x),
则函数f(x)叫周期函数;非零常数T叫做这个函数的周期.
①周期函数的周期不唯一.
②若f(x)的所有周期中存在一个最小正数,
则该最小正数叫f(x)的最小正周期.
求三角函数的周期——定义法
三角函数的周期——公式法
求三角函数的周期——公式法、图象法
图象法
利用函数周期求值
Key:利用周期定义将数化到已知区间
抽象函数的周期
抽象函数的周期
2
抽象函数的周期
2.奇偶性
奇函数
偶函数
奇函数
奇函数
3.单调性
3.单调性
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
复合函数的单调性:
若原函数y=f[g(x)]由内层函数t=g(x)和外层函数y=f(t)复合而成.
则原函数的单调性满足“同增异减”原则.
内外层在I上单调性同,则原函数在I上增;
内外层在I上单调性不同,则原函数在I上减.
复合函数的单调性:
“同增异减”原则
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
“同增异减”
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
是由y=cosx左移π/3
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
求完整增区间I
赋k,求I与[-2π,2π]的交集
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
求完整减区间I
赋k,求I与[0,π]的交集
3.单调性——比较大小
用诱导公式把角化正&化小,化到同一单调区间内
3.单调性——y=Asin(wx+φ)或y=Acos(wx+φ)
4.最值
三角函数在对称轴取得最大或最小值
4.最值——①求R上的值域
4.最值——②求指定区间上的值域(整体法)
y=sint的图象
4.最值——②求指定区间上的值域(换元法)
换元
习题课
求三角函数的对称轴或对称中心
基础知识:①y=sinx的对称轴为
对称中心为
②y=cosx的对称轴为
对称中心为
③y=tanx的对称中心为
正余弦函数在对称轴处取得最值
求三角函数的对称轴或对称中心
基础知识:①y=sinx的对称轴为
对称中心为
②y=cosx的对称轴为
对称中心为
③y=tanx的对称中心为
正余弦函数在对称轴处取得最值
求x得对称轴
求x得对称中心
求x得对称中心
[注]对称轴应写为“x=… , k∈Z”,对称中心应写为“(… , 0),k∈Z”
求三角函数的对称轴或对称中心
三角函数的对称性与奇偶性
三角函数的单调性
三角函数的单调性
第五章 《三角函数》
5.4.3正切函数的性质与图象
正切函数y=tanx的性质
1.定义域:
3.周期性:
2.奇偶性:
奇函数
4.图象:
正切函数y=tanx的图象
正切函数y=tanx的性质
x
y
1
-1
4.图象:
5.单调性:
无最值
正切函数y=tanx的性质
4.图象:
5.单调性:
6.对称中心:
无最值
运用:解不等式
运用:正切函数的性质
运用:正切函数的性质
运用:正切函数的性质
FIGHTING
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
