12.2 第4课时 “斜边、直角边” 课件(共19页)
文档属性
| 名称 | 12.2 第4课时 “斜边、直角边” 课件(共19页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 09:39:02 | ||
图片预览





文档简介
(共19张PPT)
12.2三角形全等的判定
第4课时 “斜边、直角边”
精品同步教学课件
SSS
SAS
ASA
AAS
旧知:我们学过的判定三角形全等的方法
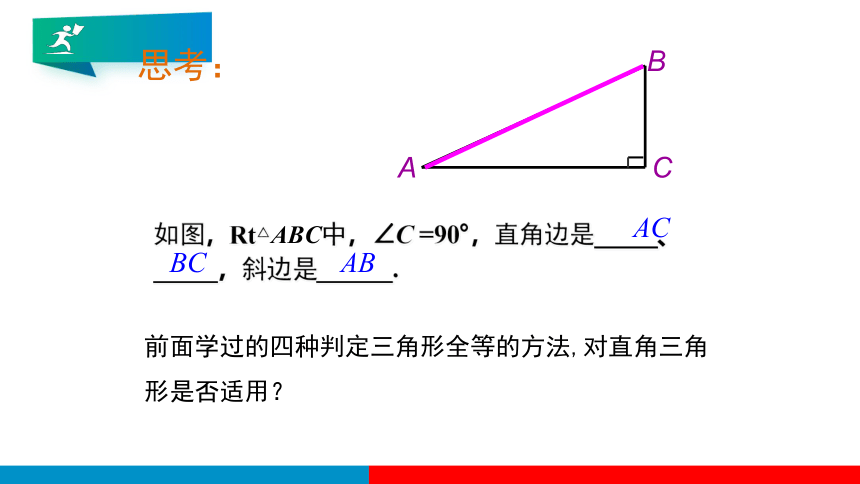
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考:
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
A
B
C
A′
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
口答:
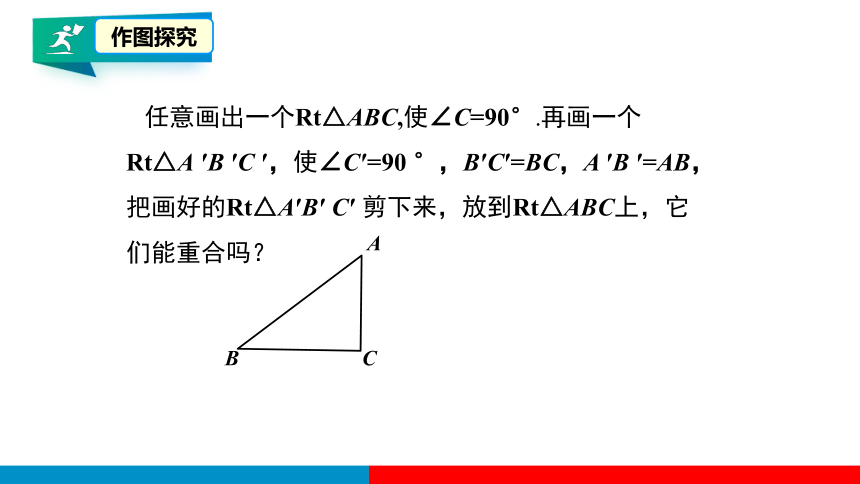
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
作图探究
知识要点
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
HL
×
SAS
AAS
AAS
判一判
典例精析
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C=∠D=90°
AB=BA,
AC=BD,
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
变式1: 如图, ∠ACB =∠ADB=90°,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”定理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
判定两个三角形全等常用的思路方法如下表
已知对应相等的元素 可选择的 判定方法 需寻找的条件
锐角 三角 形或 钝角 三角 形 两边(SS) SSS 或SAS 可证第三边对应相等或证两边的夹角对应相等
一边及其邻角(SA) SAS 或ASA 或AAS 可证已知角的另一边对应相等或证已知边的另一邻角对应相等或证已知边的对角对应相等
一边及其对角(SA) AAS 可证另一角对应相等
两角(AA) ASA 或AAS 可证两角的夹边对应相等或证一相等角的对边对应相等
直 角 三 角 形 一锐角(A) ASA 或AAS 可证直角与已知锐角的夹边对应相等或证已知锐角(或直角)的对边对应相等
斜边(H) HL 或AAS 可证一条直角边对应相等或证一锐角对应相等
一直角边 (L) HL 或ASA 或AAS 或 SAS 可证斜边对应相等或证与已知边相邻的锐角对应相等或证已知边所对的锐角对应相等或证另一直角边对应相等
如图12.2-12,AC ⊥ BC,AD ⊥ BD,AD=BC,CE ⊥ AB,DF ⊥ AB,垂足分别是E,F. 求证CE=DF.
解题秘方:利用“HL”证明两个直角三角形全等,为证明两条线段相等创造条件.
例2
证明:∵ AC ⊥ BC,AD ⊥ BD,
∴∠ ACB= ∠ BDA=90°.
在Rt △ ABC 和Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD(HL).
∴∠ CBE= ∠ DAF.
∵ CE ⊥ AB,DF ⊥ AB,
∴∠ CEB=90°,∠ DFA=90°.
在△ BCE 和△ ADF 中,
∴△ BCE ≌△ ADF(AAS).
∴ CE=DF.
练习. 如图, 小明和小芳以相同的速度分别同时从A,B 出发, 小明沿AC 行走,小芳沿BD 行走, 并同时到达C,D. 若CB ⊥ AB,DA ⊥ AB, 则CB与DA相等吗?为什么?
https://www.21cnjy.com/help/help_extract.php
12.2三角形全等的判定
第4课时 “斜边、直角边”
精品同步教学课件
SSS
SAS
ASA
AAS
旧知:我们学过的判定三角形全等的方法
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考:
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
A
B
C
A′
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
口答:
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
作图探究
知识要点
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
HL
×
SAS
AAS
AAS
判一判
典例精析
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C=∠D=90°
AB=BA,
AC=BD,
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
变式1: 如图, ∠ACB =∠ADB=90°,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”定理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
判定两个三角形全等常用的思路方法如下表
已知对应相等的元素 可选择的 判定方法 需寻找的条件
锐角 三角 形或 钝角 三角 形 两边(SS) SSS 或SAS 可证第三边对应相等或证两边的夹角对应相等
一边及其邻角(SA) SAS 或ASA 或AAS 可证已知角的另一边对应相等或证已知边的另一邻角对应相等或证已知边的对角对应相等
一边及其对角(SA) AAS 可证另一角对应相等
两角(AA) ASA 或AAS 可证两角的夹边对应相等或证一相等角的对边对应相等
直 角 三 角 形 一锐角(A) ASA 或AAS 可证直角与已知锐角的夹边对应相等或证已知锐角(或直角)的对边对应相等
斜边(H) HL 或AAS 可证一条直角边对应相等或证一锐角对应相等
一直角边 (L) HL 或ASA 或AAS 或 SAS 可证斜边对应相等或证与已知边相邻的锐角对应相等或证已知边所对的锐角对应相等或证另一直角边对应相等
如图12.2-12,AC ⊥ BC,AD ⊥ BD,AD=BC,CE ⊥ AB,DF ⊥ AB,垂足分别是E,F. 求证CE=DF.
解题秘方:利用“HL”证明两个直角三角形全等,为证明两条线段相等创造条件.
例2
证明:∵ AC ⊥ BC,AD ⊥ BD,
∴∠ ACB= ∠ BDA=90°.
在Rt △ ABC 和Rt △ BAD 中,
∴ Rt △ ABC ≌ Rt △ BAD(HL).
∴∠ CBE= ∠ DAF.
∵ CE ⊥ AB,DF ⊥ AB,
∴∠ CEB=90°,∠ DFA=90°.
在△ BCE 和△ ADF 中,
∴△ BCE ≌△ ADF(AAS).
∴ CE=DF.
练习. 如图, 小明和小芳以相同的速度分别同时从A,B 出发, 小明沿AC 行走,小芳沿BD 行走, 并同时到达C,D. 若CB ⊥ AB,DA ⊥ AB, 则CB与DA相等吗?为什么?
https://www.21cnjy.com/help/help_extract.php
