12.3 第1课时 角平分线的性质 课件(共26页)
文档属性
| 名称 | 12.3 第1课时 角平分线的性质 课件(共26页) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 15:43:18 | ||
图片预览


文档简介
(共26张PPT)
12.3 角的平分线的性质
第1课时 角平分线的性质
精品同步教学课件
问题1:在纸上画一个角,你能得到这个角的平分
线吗?
导入新课
用量角器度量,也可用折纸的方法.
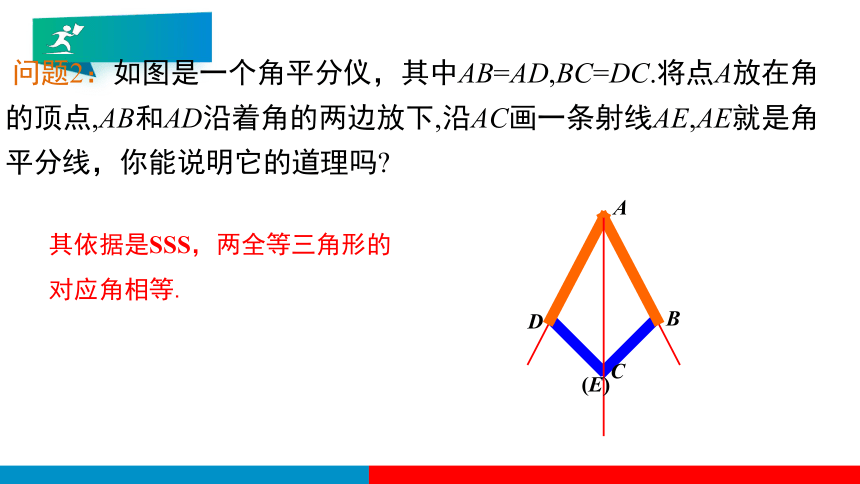
问题2:如图是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
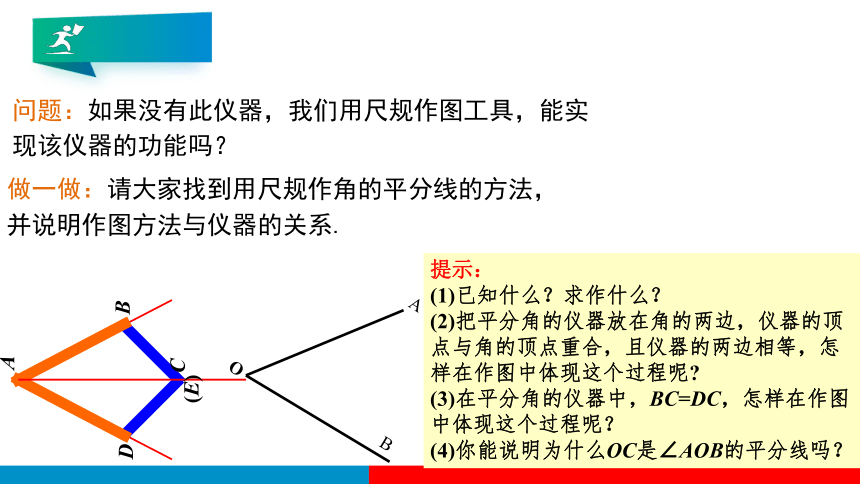
问题:如果没有此仪器,我们用尺规作图工具,能实现该仪器的功能吗?
A
B
O
做一做:请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示:
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
A
B
C
(E)
D
A
B
M
N
C
O
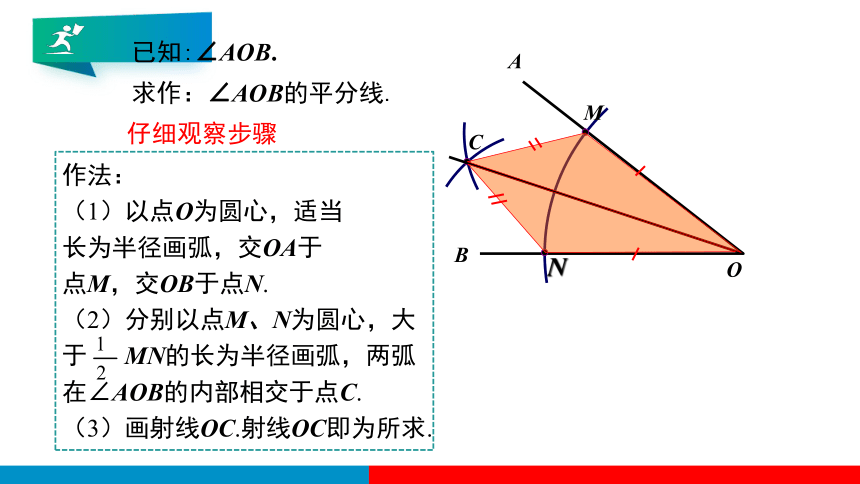
已知:∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作法:
(1)以点O为圆心,适当
长为半径画弧,交OA于
点M,交OB于点N.
(2)分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
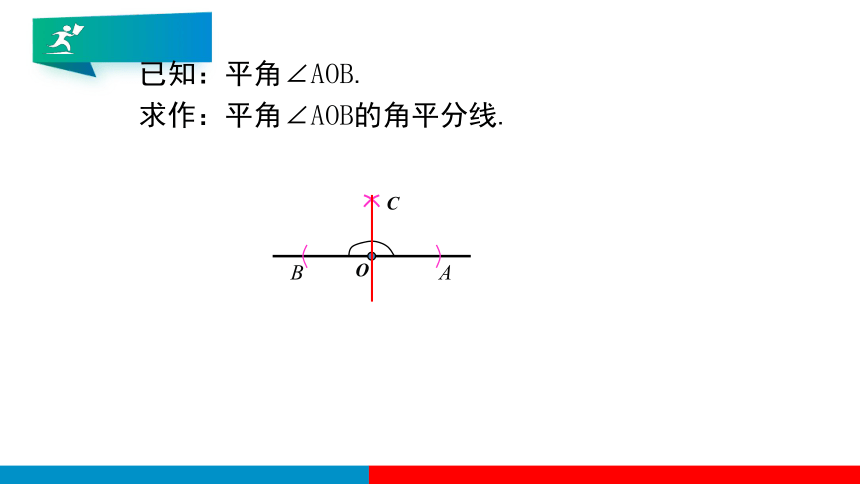
已知:平角∠AOB.
求作:平角∠AOB的角平分线.
A
B
O
C
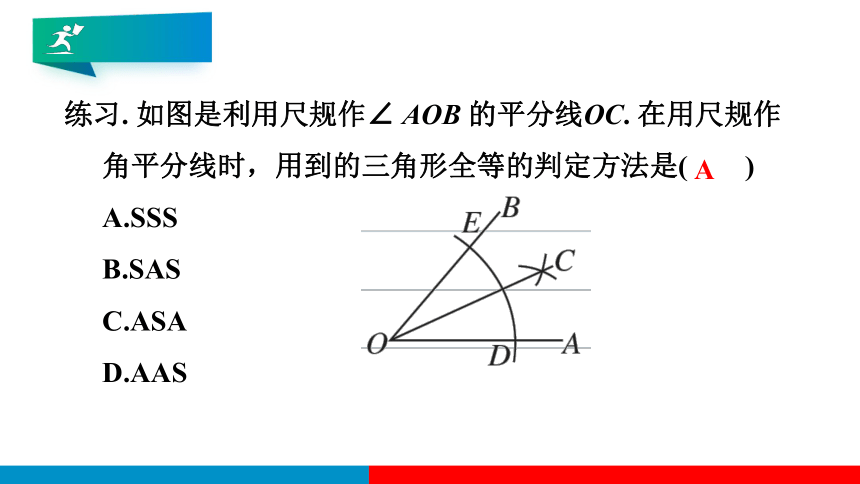
练习. 如图是利用尺规作∠ AOB 的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS
B.SAS
C.ASA
D.AAS
A
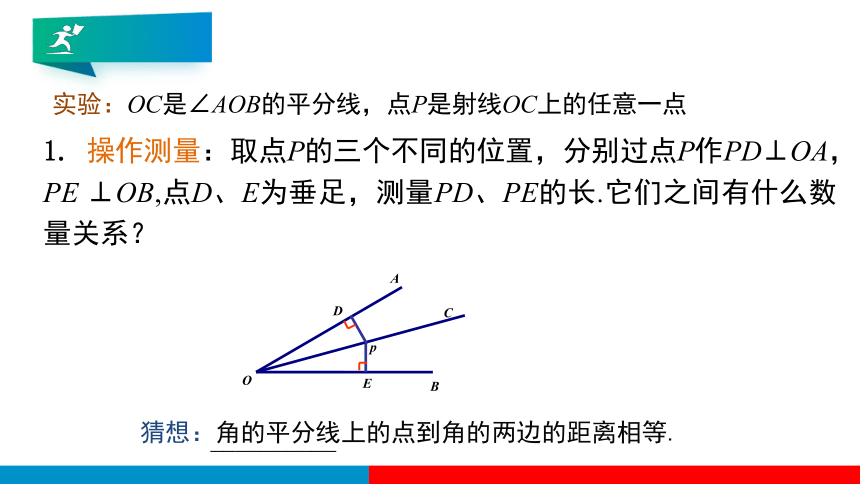
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.它们之间有什么数量关系?
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
C
O
B
A
PD=PE
p
D
E
实验:OC是∠AOB的平分线,点P是射线OC上的任意一点
猜想:角的平分线上的点到角的两边的距离相等.
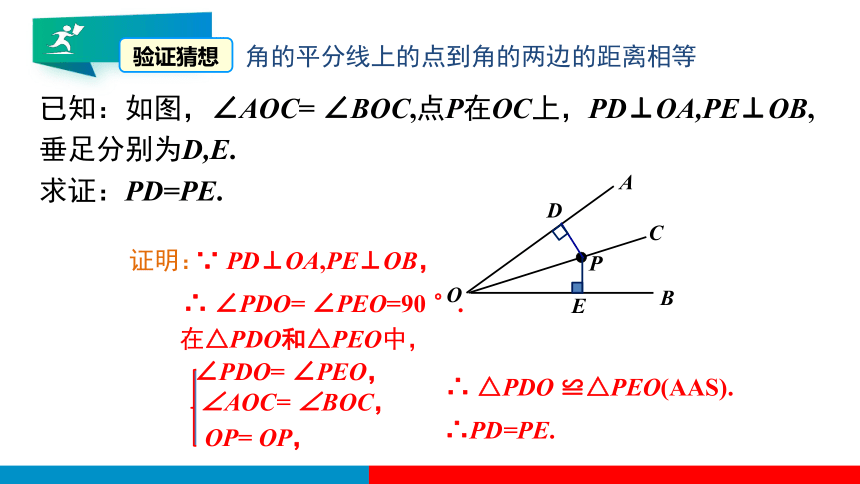
验证猜想
已知:如图,∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证明过程.
方法归纳
性质定理:角的平分线上的点到角的两边的距离相等.
定理的作用:
证明线段相等(角分双垂得等距)
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE.
PD⊥OA于D,PE⊥OB于E,
B
A
D
O
P
E
C
判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知),
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
例1:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,PD=4 cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
A
B
C
P
变式:如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=m, AB=14.
(1)则点P到AB的距离为_______(用含m的式子表示);
(2)若AC=10,△ABP的面积与
△ACP的面积比是多少?
(3)若AC=10,△ABC的面积是48,求m的值
D
m
温馨提示:存在一条垂线段———构造应用
如图12.3-4,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P 为OD 上一点,PM ⊥ BD,PN ⊥ AD,垂足分别为M,N. 求证:PM=PN.
例2
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
证明:∵OD平分∠EOF,∴∠BOD=∠AOD.
在△ BOD 和△ AOD 中,
∴△ BOD ≌△ AOD(SAS).
∴∠ BDO= ∠ ADO,即DO 平分∠ BDA.
又∵ P 为DO 上一点,且PM ⊥ BD,PN ⊥ AD,
∴ PM=PN.
B
练习.[中考·台州] 如图,点P 是∠ AOB 的平分线OC 上一点,PD ⊥ OB,垂足为D. 若PD=2,则点P 到边OA 的距离是( )
A. 1 B. 2
C. D. 4
如图12.3-5,在△ ABC 中,∠ C=90°,AC=BC,AD平分∠ CAB,交BC 于点D,DE ⊥ AB,垂足为E. 若AB=8 cm,求△ DEB 的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB 的周长转化为线段AB 的长.
例 3
解:在△ ABC 中,∠ C=90°,
∴ DC ⊥ AC.
又∵ DE ⊥ AB,AD 平分∠ CAB,
∴ DC=DE.
在Rt △ ACD 和Rt △ AED 中,
∴ Rt △ ACD ≌ Rt △ AED(HL). ∴ AC=AE.
∵ AC=BC,∴ AE=BC.
∴△ DEB 的周长=DE+DB+EB=
DC+DB+EB=BC+EB=AE+EB=AB=8 cm.
练习. 如图,在△ ABC 中,∠ C=90 °,AD 平分∠ BAC,DE ⊥ AB 于点E,有下列结论:
① CD=ED;② AC+BE=AB;
③∠ BDE= ∠ BAC;④ DA 平分∠ CDE.
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
D
如图12.3-6,BD 是△ ABC 的角平分线,DE ⊥ AB 于E,S△ ABC=90 cm2,AB=18 cm,BC=12 cm,求DE 的长.
例4
解题秘方:紧扣总面积等于各部分面积的和求解.
解:过点D 作DF ⊥ BC,垂足为F,如图12.3-6.
∵ BD 是∠ ABC 的平分线,DE ⊥ AB,∴ DE=DF.
又∵ S △ ABC=S △ ABD+S △ BDC=
×18×DE+ ×12×DF=90 (cm2),
∴ DE=6 cm,即DE 的长为6 cm.
练习[中考· 湖州] 如图,已知在四边形ABCD中, ∠ BCD=90 °,BD平分∠ ABC,AB=6,BC=9,CD=4, 则四边形ABCD 的面积是( )
A.24 B.30
C.36 D.42
B
https://www.21cnjy.com/help/help_extract.php
12.3 角的平分线的性质
第1课时 角平分线的性质
精品同步教学课件
问题1:在纸上画一个角,你能得到这个角的平分
线吗?
导入新课
用量角器度量,也可用折纸的方法.
问题2:如图是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
问题:如果没有此仪器,我们用尺规作图工具,能实现该仪器的功能吗?
A
B
O
做一做:请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示:
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
A
B
C
(E)
D
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作法:
(1)以点O为圆心,适当
长为半径画弧,交OA于
点M,交OB于点N.
(2)分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
已知:平角∠AOB.
求作:平角∠AOB的角平分线.
A
B
O
C
练习. 如图是利用尺规作∠ AOB 的平分线OC. 在用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS
B.SAS
C.ASA
D.AAS
A
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.它们之间有什么数量关系?
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结:__________
C
O
B
A
PD=PE
p
D
E
实验:OC是∠AOB的平分线,点P是射线OC上的任意一点
猜想:角的平分线上的点到角的两边的距离相等.
验证猜想
已知:如图,∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1.明确命题中的已知和求证;
2.根据题意,画出图形,并用数学符号表示已知和求证;
3.经过分析,找出由已知推出要证的结论的途径,写出证明过程.
方法归纳
性质定理:角的平分线上的点到角的两边的距离相等.
定理的作用:
证明线段相等(角分双垂得等距)
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE.
PD⊥OA于D,PE⊥OB于E,
B
A
D
O
P
E
C
判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知),
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
例1:如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,PD=4 cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
A
B
C
P
变式:如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=m, AB=14.
(1)则点P到AB的距离为_______(用含m的式子表示);
(2)若AC=10,△ABP的面积与
△ACP的面积比是多少?
(3)若AC=10,△ABC的面积是48,求m的值
D
m
温馨提示:存在一条垂线段———构造应用
如图12.3-4,OD平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P 为OD 上一点,PM ⊥ BD,PN ⊥ AD,垂足分别为M,N. 求证:PM=PN.
例2
解题秘方:在图中找出符合角的平分线的性质的模型,利用角的平分线的性质证线段相等.
证明:∵OD平分∠EOF,∴∠BOD=∠AOD.
在△ BOD 和△ AOD 中,
∴△ BOD ≌△ AOD(SAS).
∴∠ BDO= ∠ ADO,即DO 平分∠ BDA.
又∵ P 为DO 上一点,且PM ⊥ BD,PN ⊥ AD,
∴ PM=PN.
B
练习.[中考·台州] 如图,点P 是∠ AOB 的平分线OC 上一点,PD ⊥ OB,垂足为D. 若PD=2,则点P 到边OA 的距离是( )
A. 1 B. 2
C. D. 4
如图12.3-5,在△ ABC 中,∠ C=90°,AC=BC,AD平分∠ CAB,交BC 于点D,DE ⊥ AB,垂足为E. 若AB=8 cm,求△ DEB 的周长.
解题秘方:运用角的平分线的性质及全等三角形的性质,将△ DEB 的周长转化为线段AB 的长.
例 3
解:在△ ABC 中,∠ C=90°,
∴ DC ⊥ AC.
又∵ DE ⊥ AB,AD 平分∠ CAB,
∴ DC=DE.
在Rt △ ACD 和Rt △ AED 中,
∴ Rt △ ACD ≌ Rt △ AED(HL). ∴ AC=AE.
∵ AC=BC,∴ AE=BC.
∴△ DEB 的周长=DE+DB+EB=
DC+DB+EB=BC+EB=AE+EB=AB=8 cm.
练习. 如图,在△ ABC 中,∠ C=90 °,AD 平分∠ BAC,DE ⊥ AB 于点E,有下列结论:
① CD=ED;② AC+BE=AB;
③∠ BDE= ∠ BAC;④ DA 平分∠ CDE.
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
D
如图12.3-6,BD 是△ ABC 的角平分线,DE ⊥ AB 于E,S△ ABC=90 cm2,AB=18 cm,BC=12 cm,求DE 的长.
例4
解题秘方:紧扣总面积等于各部分面积的和求解.
解:过点D 作DF ⊥ BC,垂足为F,如图12.3-6.
∵ BD 是∠ ABC 的平分线,DE ⊥ AB,∴ DE=DF.
又∵ S △ ABC=S △ ABD+S △ BDC=
×18×DE+ ×12×DF=90 (cm2),
∴ DE=6 cm,即DE 的长为6 cm.
练习[中考· 湖州] 如图,已知在四边形ABCD中, ∠ BCD=90 °,BD平分∠ ABC,AB=6,BC=9,CD=4, 则四边形ABCD 的面积是( )
A.24 B.30
C.36 D.42
B
https://www.21cnjy.com/help/help_extract.php
