12.3 第2课时 角平分线的判定 课件(共21页)
文档属性
| 名称 | 12.3 第2课时 角平分线的判定 课件(共21页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 15:43:18 | ||
图片预览



文档简介
(共21张PPT)
12.3 角的平分线的性质
第2课时 角平分线的判定
精品同步教学课件
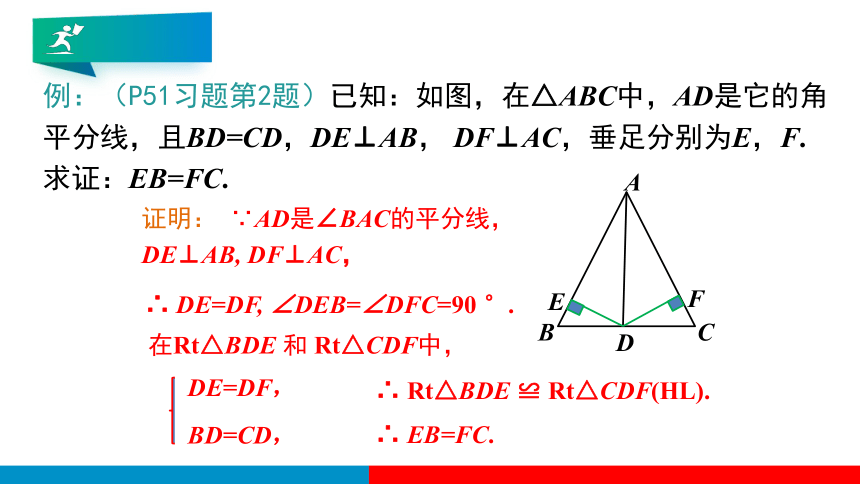
例:(P51习题第2题)已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB, DF⊥AC,垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
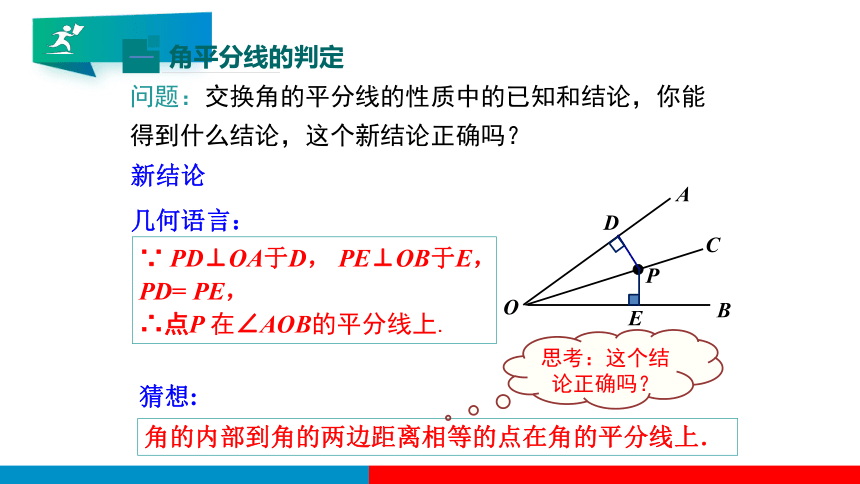
我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
角平分线的判定
一
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
∵ PD⊥OA于D, PE⊥OB于E,PD= PE,
∴点P 在∠AOB的平分线上.
新结论
几何语言:
猜想:
思考:这个结论正确吗?
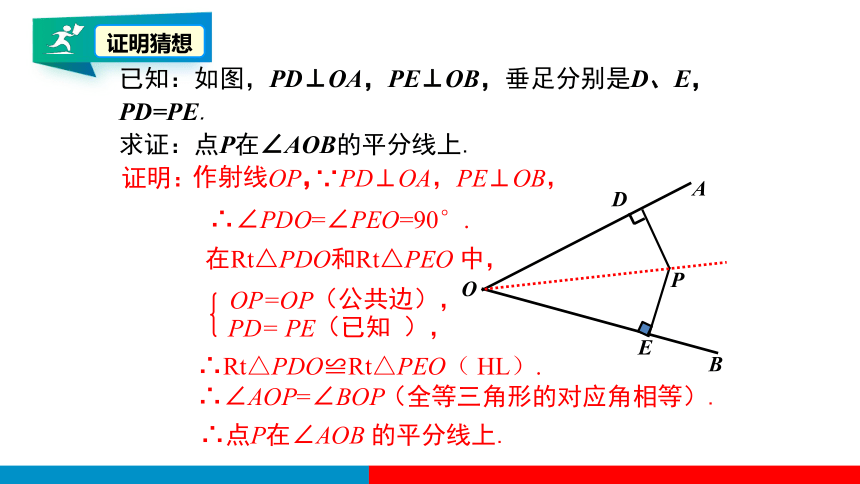
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的平分线上.
证明:
作射线OP,
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
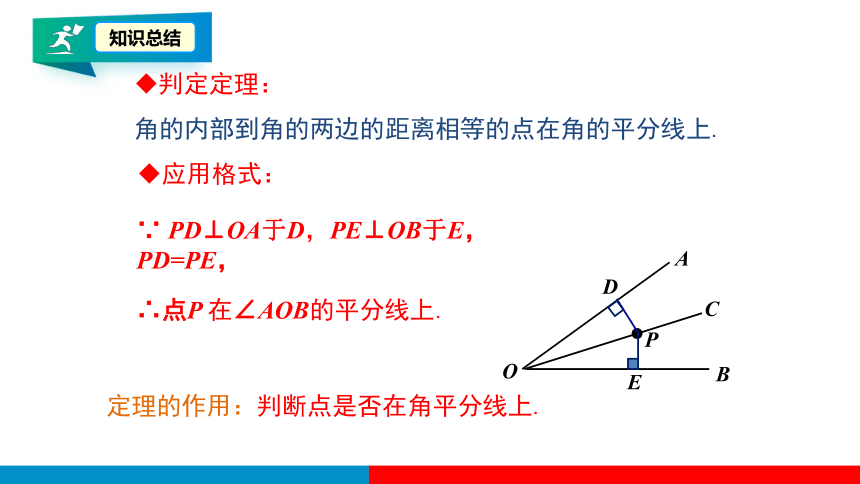
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA于D,PE⊥OB于E,PD=PE,
∴点P 在∠AOB的平分线上.
知识总结
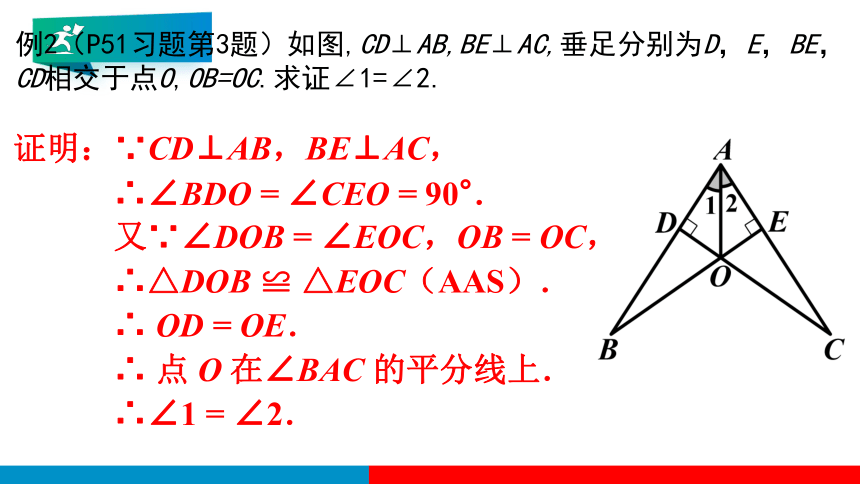
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO = ∠CEO = 90°.
又∵∠DOB = ∠EOC,OB = OC,
∴△DOB ≌ △EOC(AAS).
∴ OD = OE.
∴ 点 O 在∠BAC 的平分线上.
∴∠1 = ∠2.
例2(P51习题第3题)如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC.求证∠1=∠2.
典例精析
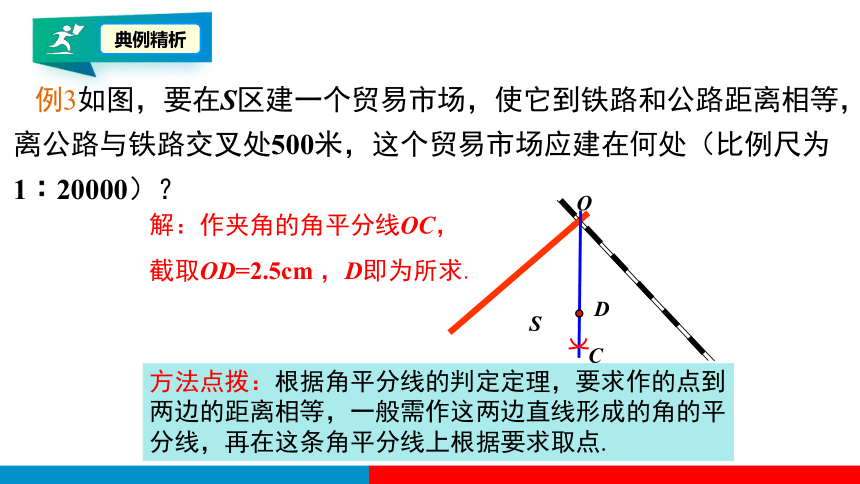
例3如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个贸易市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
练习
如图12.3-9,BE=CF,BF ⊥ AC 于点F,CE ⊥ AB 于点E,BF 和CE 交于点D. 求证:AD 平分∠ BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,
紧扣点在角的内部且点到角两边的距离相等进行证明.
例4
证明:∵ BF ⊥ AC,CE ⊥ AB,
∴∠ DEB= ∠ DFC=90°.
在△ BDE 和△ CDF 中,
∴△ BDE ≌△ CDF(AAS). ∴ DE=DF.
又∵ BF ⊥ AC,CE ⊥ AB,∴ AD 平分∠ BAC.
练习. 如图, 在△ ABC中,BD ⊥ AC 于D,CE ⊥ AB 于E, 且BO=CO. 求证:AO 平分∠ BAC.
练习. 如图,D,E,F 分别是△ ABC 三边上的点,CE=BF,△ DCE和△ DBF的面积相等. 求证:AD平分∠ BAC.
如图12.3-10,∠ MAC 和∠ NCA 是△ ABC 的外角,
∠ ABC 的平分线BD 与∠ MAC 的平分线AD 交于点D.求证:CD 平分∠ ACN.
解题秘方:紧扣“到CA,CN 的距离相等的点在∠ ACN 的平分线上”进行证明.
例 5
证明: 如图12.3-10, 过点D 作DE ⊥ BM 于点E,
DF ⊥ BN 于点F,DG ⊥ AC 于点G.
∵ BD 平分∠ ABC,∴ DE=DF.
∵ AD 平分∠ MAC,
∴ DE=DG. ∴ DG=DF,
∴ CD 平分∠ ACN.
https://www.21cnjy.com/help/help_extract.php
12.3 角的平分线的性质
第2课时 角平分线的判定
精品同步教学课件
例:(P51习题第2题)已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB, DF⊥AC,垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
我们知道,角平分线上的点到角的两边的距离相等.那么到角的两边的距离相等的点是否在角的平分线上呢?
角平分线的判定
一
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
∵ PD⊥OA于D, PE⊥OB于E,PD= PE,
∴点P 在∠AOB的平分线上.
新结论
几何语言:
猜想:
思考:这个结论正确吗?
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
求证:点P在∠AOB的平分线上.
证明:
作射线OP,
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA于D,PE⊥OB于E,PD=PE,
∴点P 在∠AOB的平分线上.
知识总结
证明:∵CD⊥AB,BE⊥AC,
∴∠BDO = ∠CEO = 90°.
又∵∠DOB = ∠EOC,OB = OC,
∴△DOB ≌ △EOC(AAS).
∴ OD = OE.
∴ 点 O 在∠BAC 的平分线上.
∴∠1 = ∠2.
例2(P51习题第3题)如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC.求证∠1=∠2.
典例精析
例3如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个贸易市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
练习
如图12.3-9,BE=CF,BF ⊥ AC 于点F,CE ⊥ AB 于点E,BF 和CE 交于点D. 求证:AD 平分∠ BAC.
解题秘方:利用角的平分线的判定定理证明角平分线时,
紧扣点在角的内部且点到角两边的距离相等进行证明.
例4
证明:∵ BF ⊥ AC,CE ⊥ AB,
∴∠ DEB= ∠ DFC=90°.
在△ BDE 和△ CDF 中,
∴△ BDE ≌△ CDF(AAS). ∴ DE=DF.
又∵ BF ⊥ AC,CE ⊥ AB,∴ AD 平分∠ BAC.
练习. 如图, 在△ ABC中,BD ⊥ AC 于D,CE ⊥ AB 于E, 且BO=CO. 求证:AO 平分∠ BAC.
练习. 如图,D,E,F 分别是△ ABC 三边上的点,CE=BF,△ DCE和△ DBF的面积相等. 求证:AD平分∠ BAC.
如图12.3-10,∠ MAC 和∠ NCA 是△ ABC 的外角,
∠ ABC 的平分线BD 与∠ MAC 的平分线AD 交于点D.求证:CD 平分∠ ACN.
解题秘方:紧扣“到CA,CN 的距离相等的点在∠ ACN 的平分线上”进行证明.
例 5
证明: 如图12.3-10, 过点D 作DE ⊥ BM 于点E,
DF ⊥ BN 于点F,DG ⊥ AC 于点G.
∵ BD 平分∠ ABC,∴ DE=DF.
∵ AD 平分∠ MAC,
∴ DE=DG. ∴ DG=DF,
∴ CD 平分∠ ACN.
https://www.21cnjy.com/help/help_extract.php
