12.3 第3课时角平分线的性质及判定综合 课件(共19页)
文档属性
| 名称 | 12.3 第3课时角平分线的性质及判定综合 课件(共19页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 15:43:18 | ||
图片预览

文档简介
(共19张PPT)
12.3 角的平分线的性质
第3课时 角平分线的性质及判定综合
精品同步教学课件
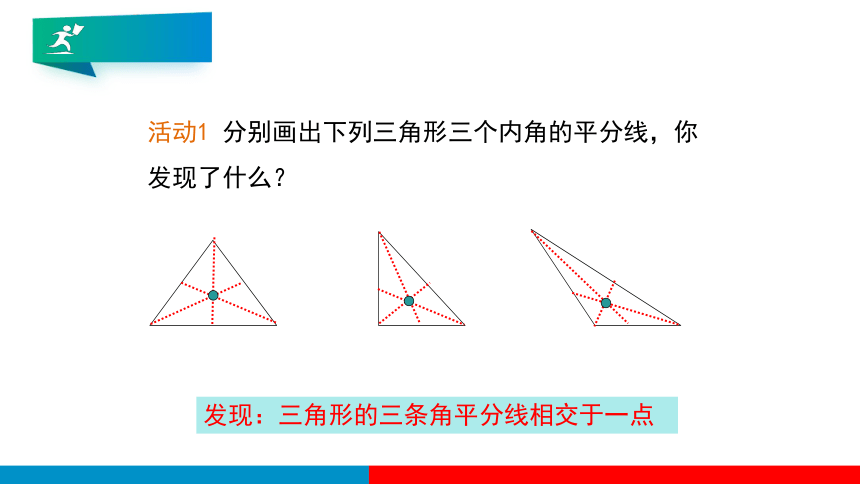
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
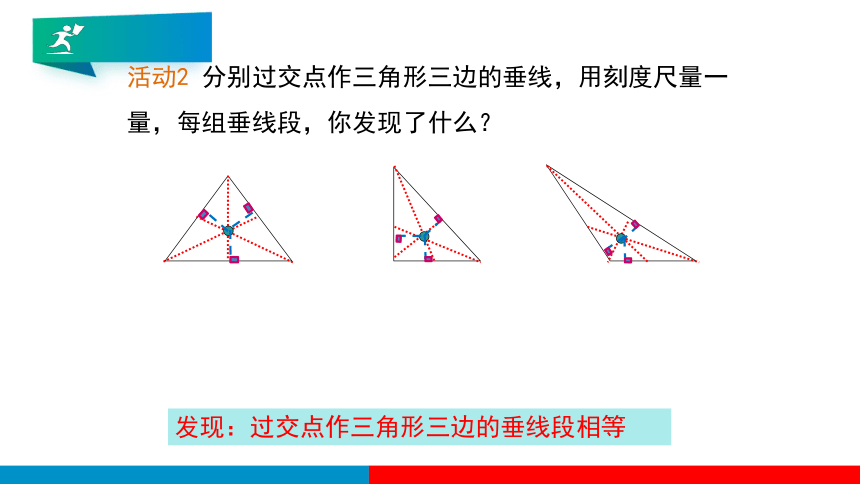
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等
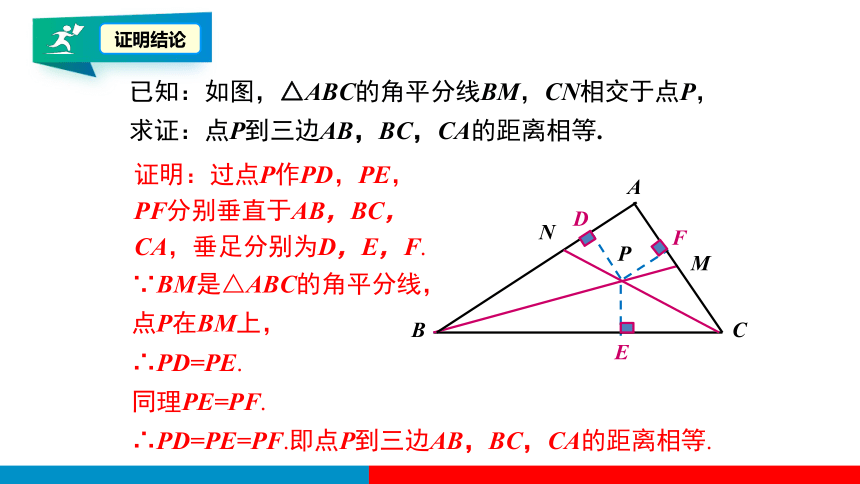
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明结论
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理PE=PF.
∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
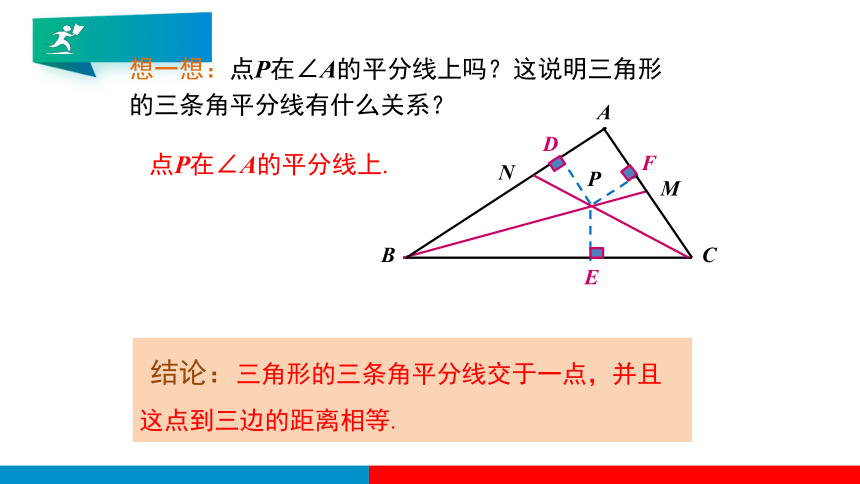
想一想:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
点P在∠A的平分线上.
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
D
E
F
A
B
C
P
N
M
M
E
N
A
B
C
P
O
D
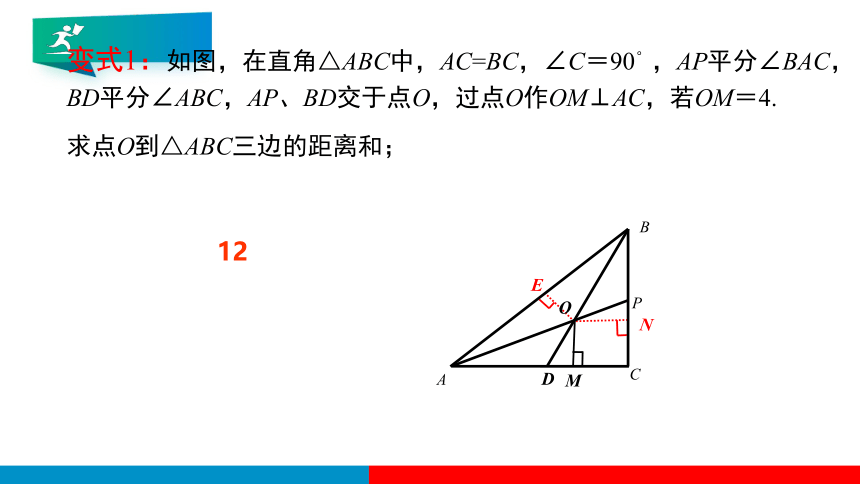
变式1:如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
求点O到△ABC三边的距离和;
12
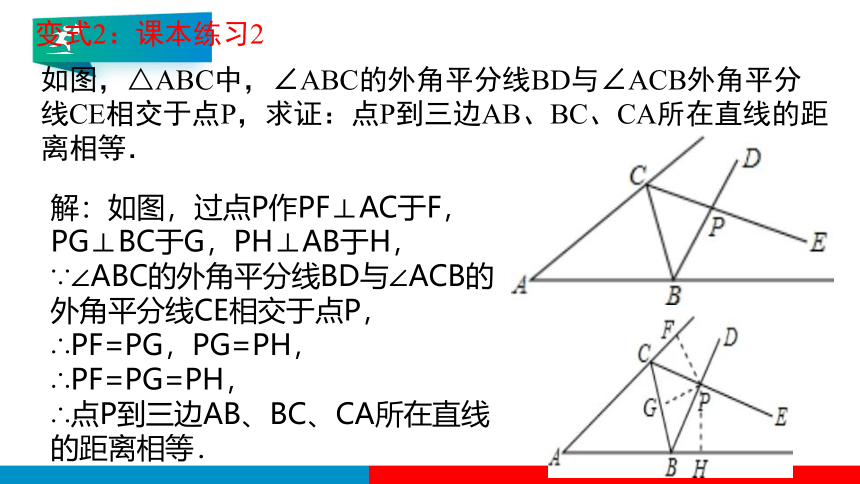
如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.
变式2:课本练习2
解:如图,过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∴点P到三边AB、BC、CA所在直线的距离相等.
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
课本练习1
如图12.3-12,在△ ABC 中,点O 是∠ ABC,∠ ACB的平分线的交点,AB+BC+AC=20. 过O 作OD ⊥ BC 于点D. 且OD=3, 求△ ABC 的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
例
解:如图12.3-12,过点O 作OE ⊥ AB 于点E,
OF ⊥ AC于点F, 连接OA.
∵点O 是∠ ABC 的平分线与∠ ACB 的平分线的交点,∴ OE=OD, OF=OD,即OE=OF=OD=3.
∴ S△ABC=S△ABO+S△BCO+S△ACO= AB·OE+ BC·
OD+ AC·OF= ×3×( AB+BC+AC)= ×3×20=30.
练习. 如图, 有一块三角形的空地ABC. 其三边长AB,AC,BC 分别为30 m,40 m,50m. 现要把它分成面积比为3 ∶ 4 ∶ 5 的三部分种植三种不同的花,请你设计一种方案,并简要说明理由.
解:方案如图.分别作∠ABC和∠ACB的平分线,两线交于点P,连接AP,则△ABP,△ACP,△BCP即为所求的三块地.
理由:∵P为△ABC的三个内角平分线的交点,
∴点P到AB,AC,BC的距离均相等.
∴△ABP,△ACP,△BCP的面积比即为它们的底边AB,AC,BC的长度的比.
1.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.为什么
解:∵PM⊥OA,PN⊥OB,
∴∠OMP = ∠ONP = 90°.
在 Rt△MOP 和 Rt△PON 中,
∴ Rt△OMP ≌ Rt△ONP(HL).
∴∠MOP = ∠NOP,
即 OP 是∠AOB 的平分线.
本节教材习题讲解
证明:∵AD 是 △ABC 的角平分线,
∴∠BAD = ∠CAD.
又∵PE∥AB,PF∥AC,
∴∠EPD = ∠BAD,∠FPD = ∠CAD.
∴∠EPD = ∠FPD.
即PD平分∠EPF.
∴点 D 到 PE 和 PF 的距离相等.
4.如图,在△ABC中,AD是它的角平分线,P是AD上的一点,PE∥
AB,交BC于点E,PF∥AC,交BC于点F,求证:点D到PE和PF的距
离相等.
证明:∵OC 平分∠AOB,且 PD⊥OA,PE⊥OB,
∴PD = PE,∠DOP = ∠EOP,∠ODP = ∠OEP=90°.
又∠DPF =∠DOP+∠ODP,∠EPF=
∠EOP+∠OEP,∴∠DPF =∠EPF.
在△DPF 和 △EPF 中,
PD = PE,∠DPF =∠EPF,PF = PF.
∴△DPF ≌ △EPF (SAS).∴DF = EF.
5.如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥
OB,垂足分别为D,E.F是OC上的另一点,连接DF,EF.求证DF=EF.
解:AD 与 EF 垂直.证明如下:
∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴ DE = DF,∠ADE = ∠ADF.
又 ∵DG = DG,
∴△GDE ≌ △GDF (SAS).
∴∠DGE = ∠DGF.
∵∠DGE + ∠DGF = 180°,
∴∠DGE = ∠DGF = 90°,即 AD⊥EF.
6.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,
F,连接EF,EF与AD相交于点G.AD与EF垂直吗 证明你的结论.
证明:如图,过点 E 作 EF⊥AD 于点 F.
∵∠B = ∠C = 90°,∴ EC⊥CD,EB⊥AB.
∵DE 平分∠ADC,∴ EF = EC.
又∵ E 是 BC 的中点,∴ EC = EB.
∴ EF = EB.
∵ EF⊥AD,EB⊥AB,
∴ 点 E 在∠DAB 的平分线上,即 AE 是∠DAB 的平分线.
F
7.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE
是∠DAB的平分线.(提示:过点E作EF⊥AD,垂足为F.)
https://www.21cnjy.com/help/help_extract.php
12.3 角的平分线的性质
第3课时 角平分线的性质及判定综合
精品同步教学课件
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明结论
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.
同理PE=PF.
∴PD=PE=PF.即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
想一想:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
点P在∠A的平分线上.
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
D
E
F
A
B
C
P
N
M
M
E
N
A
B
C
P
O
D
变式1:如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP、BD交于点O,过点O作OM⊥AC,若OM=4.
求点O到△ABC三边的距离和;
12
如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.
变式2:课本练习2
解:如图,过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∴点P到三边AB、BC、CA所在直线的距离相等.
如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
课本练习1
如图12.3-12,在△ ABC 中,点O 是∠ ABC,∠ ACB的平分线的交点,AB+BC+AC=20. 过O 作OD ⊥ BC 于点D. 且OD=3, 求△ ABC 的面积.
解题秘方:紧扣三角形内角平分线的性质,关键是内心到三边的距离相等.
例
解:如图12.3-12,过点O 作OE ⊥ AB 于点E,
OF ⊥ AC于点F, 连接OA.
∵点O 是∠ ABC 的平分线与∠ ACB 的平分线的交点,∴ OE=OD, OF=OD,即OE=OF=OD=3.
∴ S△ABC=S△ABO+S△BCO+S△ACO= AB·OE+ BC·
OD+ AC·OF= ×3×( AB+BC+AC)= ×3×20=30.
练习. 如图, 有一块三角形的空地ABC. 其三边长AB,AC,BC 分别为30 m,40 m,50m. 现要把它分成面积比为3 ∶ 4 ∶ 5 的三部分种植三种不同的花,请你设计一种方案,并简要说明理由.
解:方案如图.分别作∠ABC和∠ACB的平分线,两线交于点P,连接AP,则△ABP,△ACP,△BCP即为所求的三块地.
理由:∵P为△ABC的三个内角平分线的交点,
∴点P到AB,AC,BC的距离均相等.
∴△ABP,△ACP,△BCP的面积比即为它们的底边AB,AC,BC的长度的比.
1.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.为什么
解:∵PM⊥OA,PN⊥OB,
∴∠OMP = ∠ONP = 90°.
在 Rt△MOP 和 Rt△PON 中,
∴ Rt△OMP ≌ Rt△ONP(HL).
∴∠MOP = ∠NOP,
即 OP 是∠AOB 的平分线.
本节教材习题讲解
证明:∵AD 是 △ABC 的角平分线,
∴∠BAD = ∠CAD.
又∵PE∥AB,PF∥AC,
∴∠EPD = ∠BAD,∠FPD = ∠CAD.
∴∠EPD = ∠FPD.
即PD平分∠EPF.
∴点 D 到 PE 和 PF 的距离相等.
4.如图,在△ABC中,AD是它的角平分线,P是AD上的一点,PE∥
AB,交BC于点E,PF∥AC,交BC于点F,求证:点D到PE和PF的距
离相等.
证明:∵OC 平分∠AOB,且 PD⊥OA,PE⊥OB,
∴PD = PE,∠DOP = ∠EOP,∠ODP = ∠OEP=90°.
又∠DPF =∠DOP+∠ODP,∠EPF=
∠EOP+∠OEP,∴∠DPF =∠EPF.
在△DPF 和 △EPF 中,
PD = PE,∠DPF =∠EPF,PF = PF.
∴△DPF ≌ △EPF (SAS).∴DF = EF.
5.如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥
OB,垂足分别为D,E.F是OC上的另一点,连接DF,EF.求证DF=EF.
解:AD 与 EF 垂直.证明如下:
∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴ DE = DF,∠ADE = ∠ADF.
又 ∵DG = DG,
∴△GDE ≌ △GDF (SAS).
∴∠DGE = ∠DGF.
∵∠DGE + ∠DGF = 180°,
∴∠DGE = ∠DGF = 90°,即 AD⊥EF.
6.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,
F,连接EF,EF与AD相交于点G.AD与EF垂直吗 证明你的结论.
证明:如图,过点 E 作 EF⊥AD 于点 F.
∵∠B = ∠C = 90°,∴ EC⊥CD,EB⊥AB.
∵DE 平分∠ADC,∴ EF = EC.
又∵ E 是 BC 的中点,∴ EC = EB.
∴ EF = EB.
∵ EF⊥AD,EB⊥AB,
∴ 点 E 在∠DAB 的平分线上,即 AE 是∠DAB 的平分线.
F
7.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE
是∠DAB的平分线.(提示:过点E作EF⊥AD,垂足为F.)
https://www.21cnjy.com/help/help_extract.php
