2022-2023学年沪科版八年级数学上册11.2平面直角坐标系内图形面积的计算 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年沪科版八年级数学上册11.2平面直角坐标系内图形面积的计算 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
11.3 平面直角坐标系中图形面积的计算
阅读课本第5页例1,思考并讨论:
1.线段AB与x轴有怎样的位置关系?线段BC与y轴有怎样的位置关系?
2.线段AB、线段BC的长是多少?
3.如何计算三角形ABC的面积?
活动一
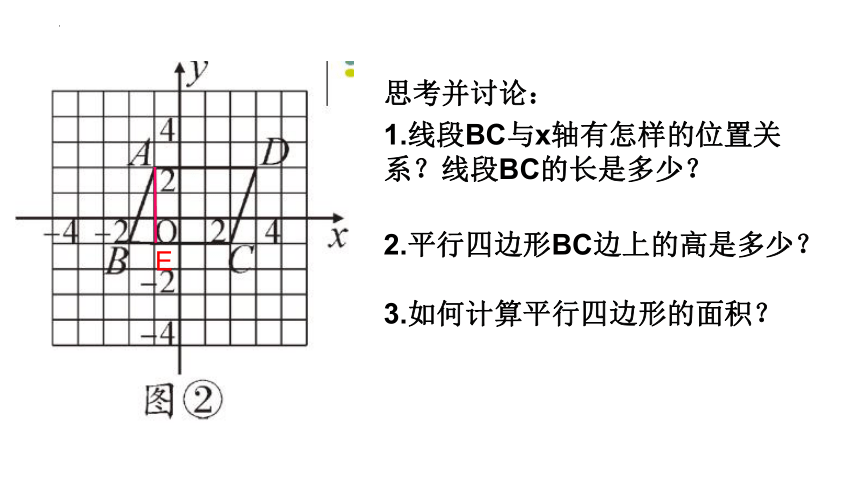
思考并讨论:
1.线段BC与x轴有怎样的位置关系?线段BC的长是多少?
2.平行四边形BC边上的高是多少?
3.如何计算平行四边形的面积?
E
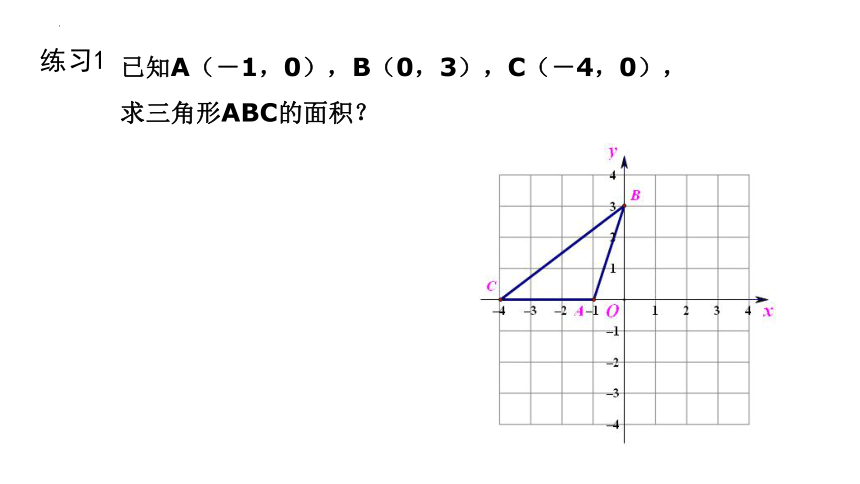
已知A(-1,0),B(0,3),C(-4,0),
求三角形ABC的面积?
练习1
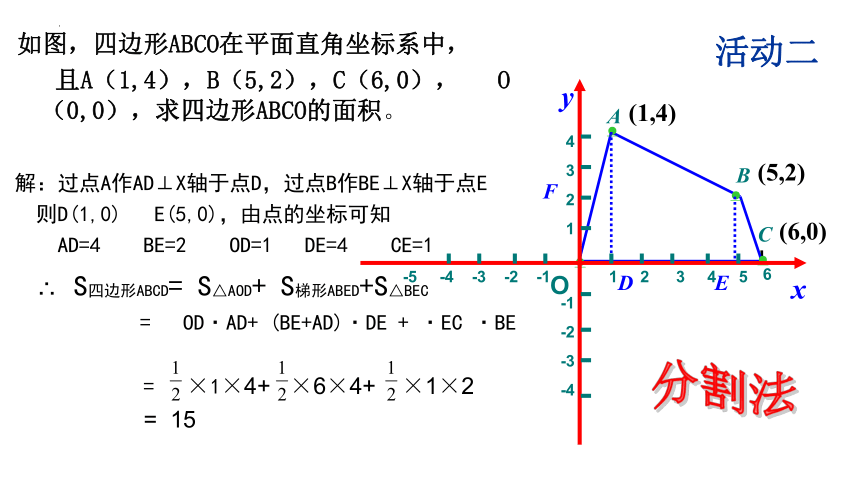
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),求四边形ABCO的面积。
6
C
B
(6,0)
(5,2)
●
●
●
●
D
E
F
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
A
(1,4)
解:过点A作AD⊥X轴于点D,过点B作BE⊥X轴于点E
则D(1,0) E(5,0),由点的坐标可知
AD=4 BE=2 OD=1 DE=4 CE=1
∴ S四边形ABCD= S△AOD+ S梯形ABED+S△BEC
= OD·AD+ (BE+AD)·DE + ·EC ·BE
= ×1×4+ ×6×4+ ×1×2
= 15
分割法
活动二
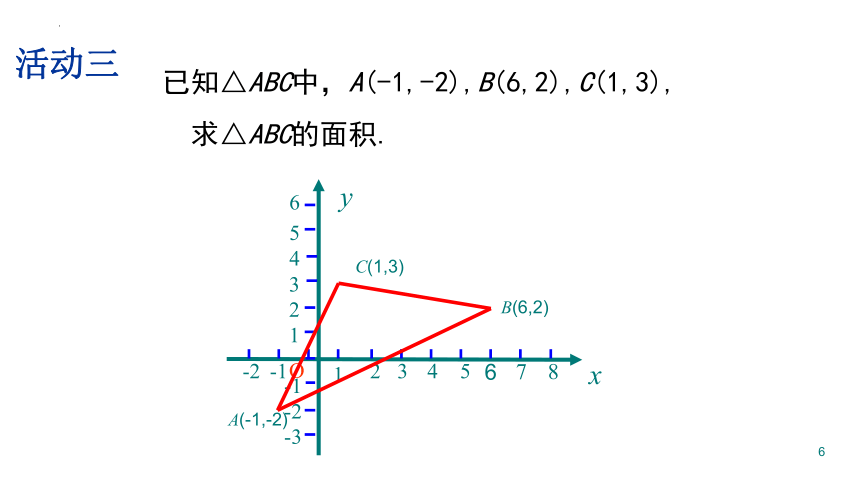
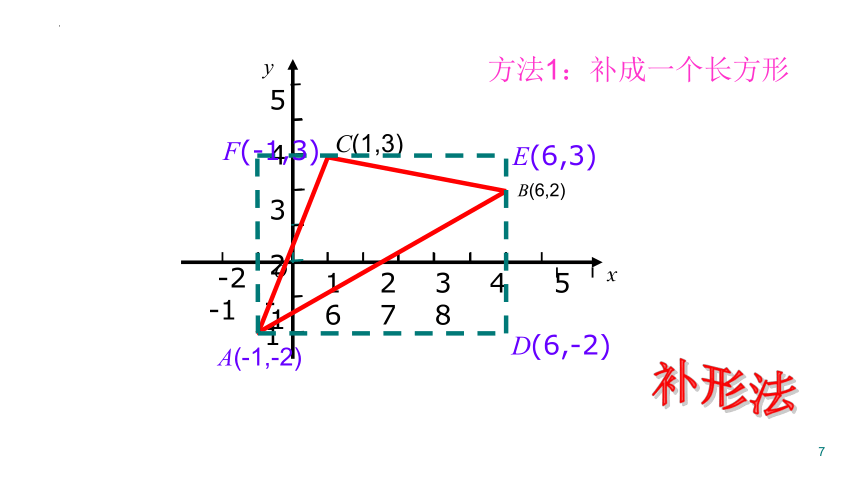
已知△ABC中,A(-1,-2),B(6,2),C(1,3),求△ABC的面积.y-36x31425-2-1O12345-2-1678A(-1,-2)B(6,2)C(1,3)活动三-1xy1 2 3 4 5 6 7 854321-2 -1OA(-1,-2)B(6,2)C(1,3)D(6,-2)E(6,3)F(-1,3)方法1:补成一个长方形补形法-1xy1 2 3 4 5 6 7 854321-2 -1OA(-1,-2)B(6,2)C(1,3)D(6,-2)E(6,3)方法2:补成一个直角梯形1、直接利用公式计算面积的图形直接应用公式计算;2、不能直接利用公式计算面积的图形,利用割补法(直割和,斜补差),将图形的面积转化为其他图形面积的和与差.思路归纳已知边长为4的正方形,请你建立一个平面直角坐标系(用尽可能多的方法),并求出各点的坐标.
说明:
(1)你是如何建立的平面直角坐标系
(如何确定的原点和坐标轴)
(2)各点坐标如何求得
活动四
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
(1)以某已知点为原点,使它的坐标为(0,0);
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
思考
如何建立适当的平面直角坐标系?
练习
如图所示,在象棋棋盘上建立直角坐标系,使“帅”位于点(-2,-2),“马”位于点(1,-2),则“兵”位于()点.
课堂小结
本节课你有什么收获?
作业布置
11.3 平面直角坐标系中图形面积的计算
阅读课本第5页例1,思考并讨论:
1.线段AB与x轴有怎样的位置关系?线段BC与y轴有怎样的位置关系?
2.线段AB、线段BC的长是多少?
3.如何计算三角形ABC的面积?
活动一
思考并讨论:
1.线段BC与x轴有怎样的位置关系?线段BC的长是多少?
2.平行四边形BC边上的高是多少?
3.如何计算平行四边形的面积?
E
已知A(-1,0),B(0,3),C(-4,0),
求三角形ABC的面积?
练习1
如图,四边形ABCO在平面直角坐标系中,
且A(1,4),B(5,2),C(6,0), O(0,0),求四边形ABCO的面积。
6
C
B
(6,0)
(5,2)
●
●
●
●
D
E
F
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
A
(1,4)
解:过点A作AD⊥X轴于点D,过点B作BE⊥X轴于点E
则D(1,0) E(5,0),由点的坐标可知
AD=4 BE=2 OD=1 DE=4 CE=1
∴ S四边形ABCD= S△AOD+ S梯形ABED+S△BEC
= OD·AD+ (BE+AD)·DE + ·EC ·BE
= ×1×4+ ×6×4+ ×1×2
= 15
分割法
活动二
已知△ABC中,A(-1,-2),B(6,2),C(1,3),求△ABC的面积.y-36x31425-2-1O12345-2-1678A(-1,-2)B(6,2)C(1,3)活动三-1xy1 2 3 4 5 6 7 854321-2 -1OA(-1,-2)B(6,2)C(1,3)D(6,-2)E(6,3)F(-1,3)方法1:补成一个长方形补形法-1xy1 2 3 4 5 6 7 854321-2 -1OA(-1,-2)B(6,2)C(1,3)D(6,-2)E(6,3)方法2:补成一个直角梯形1、直接利用公式计算面积的图形直接应用公式计算;2、不能直接利用公式计算面积的图形,利用割补法(直割和,斜补差),将图形的面积转化为其他图形面积的和与差.思路归纳已知边长为4的正方形,请你建立一个平面直角坐标系(用尽可能多的方法),并求出各点的坐标.
说明:
(1)你是如何建立的平面直角坐标系
(如何确定的原点和坐标轴)
(2)各点坐标如何求得
活动四
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
(1)以某已知点为原点,使它的坐标为(0,0);
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
0
1
2
3
4
5
-4
-3
-2
-1
3
1
2
-2
-1
-3
4
-4
x
y
B
C
D
A
思考
如何建立适当的平面直角坐标系?
练习
如图所示,在象棋棋盘上建立直角坐标系,使“帅”位于点(-2,-2),“马”位于点(1,-2),则“兵”位于()点.
课堂小结
本节课你有什么收获?
作业布置
