沪科版八年级上册11.1.2 平面内点的坐标课件(共12张PPT)
文档属性
| 名称 | 沪科版八年级上册11.1.2 平面内点的坐标课件(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 177.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
11.1.2象限内点的坐标特征
操作
1.请你建立一个平面直角坐标系;
2.在坐标系中描出以下各点:
A(-2,0) ,B(0,-3),
C(3,-4) ,D(4,0),
E(3,2) ,F(0,3).
观察
平面直角坐标系把坐
标平面分成四个部分,分
别叫做第一、二、三、四象
限.
这些象限的点各有什么特征呢?
第一象限
第四象限
第二象限
第三象限
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
y
x
写出图中的点A、B、C、D、E、F的坐标.观察你所写出的这些点的坐标,并回答:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
解:
(1)第一象限内点的符号为:(+,+)
第二象限内点的符号为:( ,+)
第三象限内点的符号为:( , )
第四象限内点的符号为:(+, )
(2)x 轴上点的纵坐标等于零;(x,0)
y 轴上点的横坐标等于零.(0,y)
注:坐标轴上的点不属于任何一个象限
原点呢?
探
究
一
练习
1.点A(-2,4)在第______象限.
2.已知点B(a,a-2)在第四象限,则a的取值范围是______.
3.已知点p(2a+3,a-4)
(1)若点p在x轴上,则a=______.
(2)若点p在y轴上,则a=______.
(3)若点p在第三象限,则a的取值范围是______.
(4)若点p在第四象限内,则a的取值范围是______.
二
04
-1.5
a<-1.5
-1.5思考:
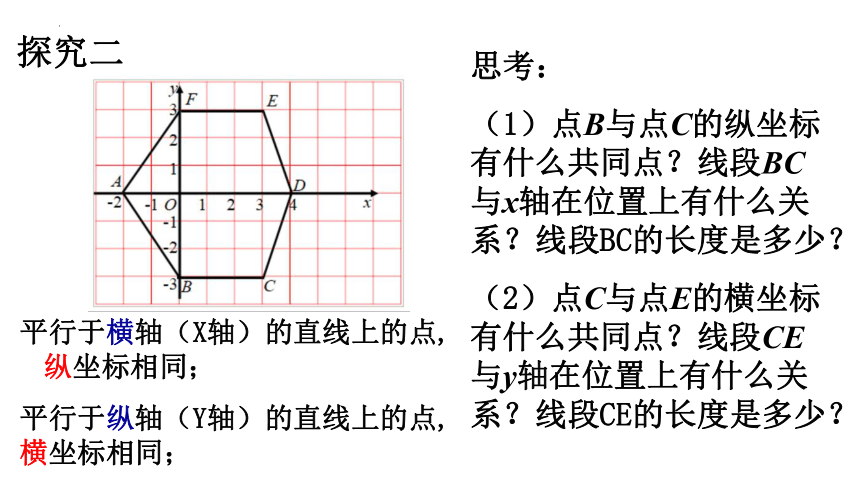
(1)点B与点C的纵坐标有什么共同点?线段BC与x轴在位置上有什么关系?线段BC的长度是多少?
(2)点C与点E的横坐标有什么共同点?线段CE与y轴在位置上有什么关系?线段CE的长度是多少?
探究二
平行于横轴(X轴)的直线上的点,纵坐标相同;
平行于纵轴(Y轴)的直线上的点,横坐标相同;
练习
已知A(3,4)、B(-2,4),作直线AB
则直线AB与x轴有什么位置关系?线段AB的长度是多少?
变式:
已知M(c,b),N(a,b),则线段MN的长度是多少?
在直角坐标平面内,
(1)第一、三象限角平分线上点的坐标有什么特点?
(2)第二、四象限角平分线上点的坐标有什么特点?
解 (1)第一、三象限角平分线上点:横坐标与纵坐标相同;(即y=x)
(2)第二、四象限角平分线上点:横坐标与纵坐标互为相反数.(即y=-x)
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
A(2,2)
D(2,-2)
(-1,1) C
(-2,-2) B
探究三
练习:已知点A(3a+2,a-3)在二、四象限的角平分线上,则a= _____.
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
1.在直角坐标系中描出点A(2,-3),A1(2,3),分别求出点A,A1到x轴的距离,并观察它们的坐标之间有什么关系?A,A1是否关于x轴对称?
2.描出点A2(-2,-3),并观察A,A2是否关于 y轴对称?两点的坐标之间有什么关系?
3.描出点A3(-2,3),并观察点A,A3是否关于原点对称?两点坐标之间又有什么关系?
解
(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数.
(3)关于原点对称的两点:横、纵坐标都互为相反数.
关于谁对称谁不变,
关于原点全变完
(-2,-3) A2
(-2,3) A3
A1(2,3)
A(2,-3)
探究四
练习
1. 与点A(3,4)关于x轴对称的点的坐标为_______,关于y轴对称的点的坐标为_______,关于原点对称的点的坐标为_____.
2.点P(-3,2),P′点是P点关于原点O的对称点,则P′点的坐标为 _____.
(3,-4)
(-3,4)
(-3,-4)
(3,-2)
课堂小结
谈谈你有什么收获?
作业布置
11.1.2象限内点的坐标特征
操作
1.请你建立一个平面直角坐标系;
2.在坐标系中描出以下各点:
A(-2,0) ,B(0,-3),
C(3,-4) ,D(4,0),
E(3,2) ,F(0,3).
观察
平面直角坐标系把坐
标平面分成四个部分,分
别叫做第一、二、三、四象
限.
这些象限的点各有什么特征呢?
第一象限
第四象限
第二象限
第三象限
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
y
x
写出图中的点A、B、C、D、E、F的坐标.观察你所写出的这些点的坐标,并回答:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
解:
(1)第一象限内点的符号为:(+,+)
第二象限内点的符号为:( ,+)
第三象限内点的符号为:( , )
第四象限内点的符号为:(+, )
(2)x 轴上点的纵坐标等于零;(x,0)
y 轴上点的横坐标等于零.(0,y)
注:坐标轴上的点不属于任何一个象限
原点呢?
探
究
一
练习
1.点A(-2,4)在第______象限.
2.已知点B(a,a-2)在第四象限,则a的取值范围是______.
3.已知点p(2a+3,a-4)
(1)若点p在x轴上,则a=______.
(2)若点p在y轴上,则a=______.
(3)若点p在第三象限,则a的取值范围是______.
(4)若点p在第四象限内,则a的取值范围是______.
二
0
-1.5
a<-1.5
-1.5
(1)点B与点C的纵坐标有什么共同点?线段BC与x轴在位置上有什么关系?线段BC的长度是多少?
(2)点C与点E的横坐标有什么共同点?线段CE与y轴在位置上有什么关系?线段CE的长度是多少?
探究二
平行于横轴(X轴)的直线上的点,纵坐标相同;
平行于纵轴(Y轴)的直线上的点,横坐标相同;
练习
已知A(3,4)、B(-2,4),作直线AB
则直线AB与x轴有什么位置关系?线段AB的长度是多少?
变式:
已知M(c,b),N(a,b),则线段MN的长度是多少?
在直角坐标平面内,
(1)第一、三象限角平分线上点的坐标有什么特点?
(2)第二、四象限角平分线上点的坐标有什么特点?
解 (1)第一、三象限角平分线上点:横坐标与纵坐标相同;(即y=x)
(2)第二、四象限角平分线上点:横坐标与纵坐标互为相反数.(即y=-x)
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
A(2,2)
D(2,-2)
(-1,1) C
(-2,-2) B
探究三
练习:已知点A(3a+2,a-3)在二、四象限的角平分线上,则a= _____.
-4 -3 -2 -1 0 1 2 3 4
1
2
3
4
-1
-2
-3
-4
1.在直角坐标系中描出点A(2,-3),A1(2,3),分别求出点A,A1到x轴的距离,并观察它们的坐标之间有什么关系?A,A1是否关于x轴对称?
2.描出点A2(-2,-3),并观察A,A2是否关于 y轴对称?两点的坐标之间有什么关系?
3.描出点A3(-2,3),并观察点A,A3是否关于原点对称?两点坐标之间又有什么关系?
解
(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数.
(3)关于原点对称的两点:横、纵坐标都互为相反数.
关于谁对称谁不变,
关于原点全变完
(-2,-3) A2
(-2,3) A3
A1(2,3)
A(2,-3)
探究四
练习
1. 与点A(3,4)关于x轴对称的点的坐标为_______,关于y轴对称的点的坐标为_______,关于原点对称的点的坐标为_____.
2.点P(-3,2),P′点是P点关于原点O的对称点,则P′点的坐标为 _____.
(3,-4)
(-3,4)
(-3,-4)
(3,-2)
课堂小结
谈谈你有什么收获?
作业布置
