椭圆与双曲线方程[上学期]
图片预览







文档简介
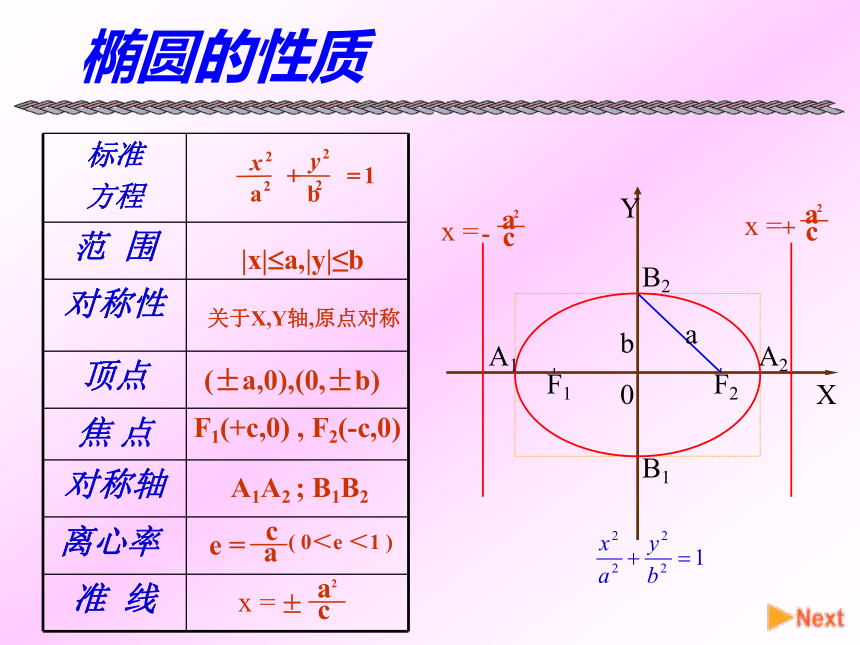
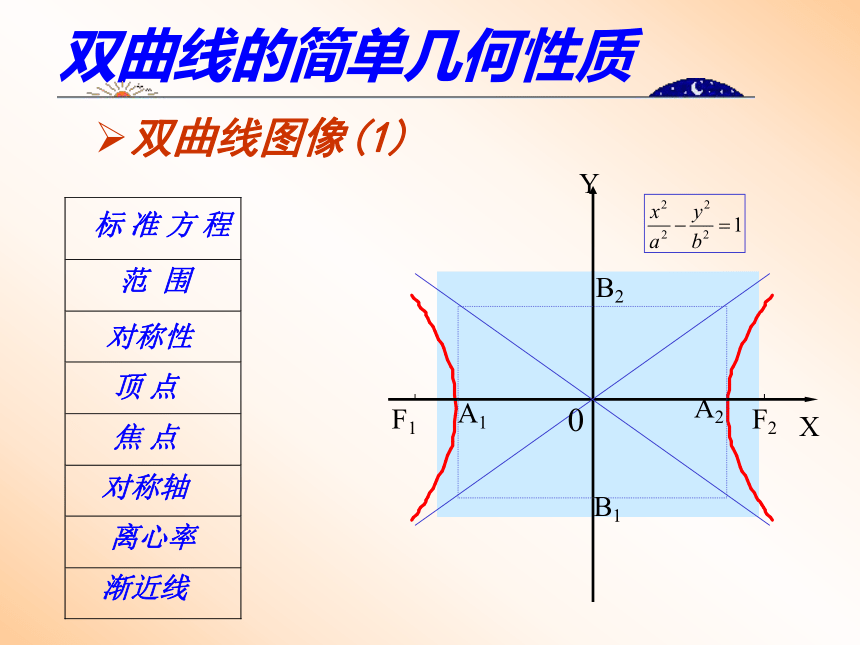
课件25张PPT。椭圆与双曲线作者: 李同刚椭圆图像和性质例题分析课堂练习双曲线图像和性质椭圆的定义 点p到两定点F1 F2的距离之和为常数(大于F1 F2距离)的点p的轨迹YX0A1A2B1B2F2F1ba椭圆的图象(1)椭圆的图象(2)YX0A1A2B1B2F2F1ab椭圆的性质|x|?a,|y|≤b关于X,Y轴,原点对称(±a,0),(0,±b)F1(+c,0) , F2(-c,0)A1A2 ; B1B2离心率( 0<e <1 )双曲线的定义 点p到两定点F1 F2的距离之差的绝对值为常数(小于F1 F2的距离)点p 的轨迹YXF1F2A1A2B1B2双曲线图像(1)双曲线的简单几何性质标 准 方 程 范 围对称性顶 点焦 点对称轴离心率 渐近线0双曲线图像与性质(1)标 准 方 程 范 围对称性顶 点焦 点对称轴离心率 渐近线x≥a 或x≤-a 关于x轴,y轴,原点对称。A1(-a,0),A2(a,0)实轴 A1A2 虚轴 B1B2 双曲线的范围x = - ax = a 双曲线的顶点 令y=0,x= ±aA1(-a,0),A2(a,0)B1 ( 0, -b ), B2 (0, b ) 双曲线的渐近线想一想:怎样较为准确的画出的图象 ?YX-44-330猜想:双曲线的渐近线MN第一象限的曲线方程 c :直线方程:设M(x,y) 是c上一点,N (x,Y)是直线..上一点。.Q= Y- y 双曲线的离心率 定义:( e>1)由可知: e越小(接近1)?双曲线开口越小(褊狭)越大 双曲线图像(2)XYF1F2OB1B2A2A1双曲线图像与性质(2)标 准 方 程 范 围对称性顶 点焦 点对称轴离心率 渐近线y≥a 或y≤-a 关于x轴,y轴,原点对称。B1(0, -a ),B2(0,a)实轴 B1B2 虚轴 A1A2例题讲解例题1 :求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:即|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)练 习 1.椭圆与双曲线|x|?a,|y|≤b|x| ≥ a,y?R对称轴:x轴,y轴
对称中心:原点对称轴:x轴,y轴
对称中心:原点(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b(-a,0) (a,0)
实轴:2a
虚轴:2b无谢谢!
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:即|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)练 习 1.椭圆与双曲线|x|?a,|y|≤b|x| ≥ a,y?R对称轴:x轴,y轴
对称中心:原点对称轴:x轴,y轴
对称中心:原点(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b(-a,0) (a,0)
实轴:2a
虚轴:2b无谢谢!
