椭圆的标准方程[上学期]
图片预览





文档简介
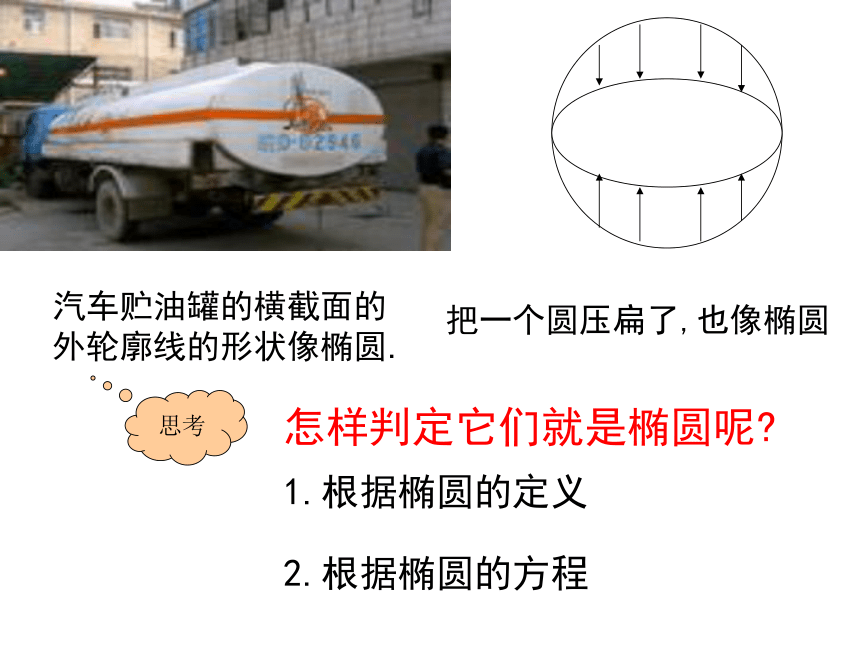
课件14张PPT。 江 苏 省 姜 堰 中 学 邱晓昇汽车贮油罐的横截面的外轮廓线的形状像椭圆.把一个圆压扁了,也像椭圆思考怎样判定它们就是椭圆呢?1.根据椭圆的定义2.根据椭圆的方程探讨如何求椭圆的方程呢?椭圆的定义: 平面内到两个定点F1、F2的距离的和等
于常数(大于F1F2)的点的轨迹叫做椭圆,两
个定点F1、F2叫做椭圆的焦点,两焦点的距
离叫做椭圆的焦距.则:即: (a2-c2)x2+a2y2=a2(a2-c2)xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足PF1+PF2
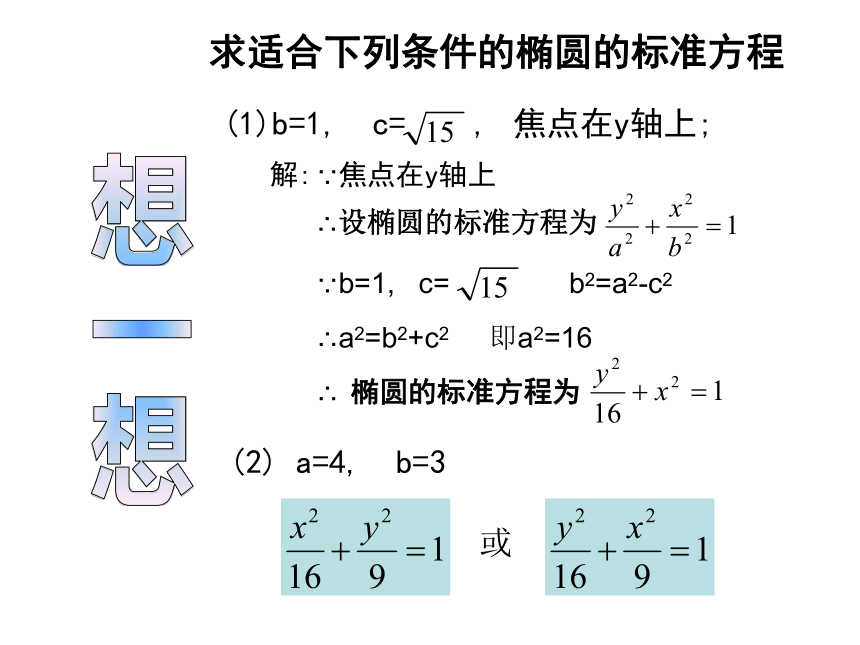
为定值,设为2a,则2a>2c则:即:O标准方程的推导b2x2+a2y2=a2b2根据已知条件,求下列椭圆的焦点坐标 想一想(1)(2)想一想求适合下列条件的椭圆的标准方程(2) a=4, b=3解:∵焦点在y轴上∴设椭圆的标准方程为∵b=1, c= b2=a2-c2∴a2=b2+c2 即a2=16或例 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.解:以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为根据题意有即因此,这个椭圆的标准方程为练 习 两个焦点分别是 (-2,0), (2,0),
且过点P求适合下列条件的椭圆的标准方程:法一: c=2法二: c=2 设椭圆标准方程为:2a=P +P 解:例 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?设所的曲线上任一点的坐标为(x,y),圆 =4上的对应点的坐标为(x’,y’),由题意可得:因为 =4所以即1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表a2-c2=b2课后研学 研究 (1) 根据椭圆标准方程你能说出它的其它性质吗? 如:椭圆的范围及a,b具有什么几何特征? (2)将圆x2+y2 = 4上的点的横坐标保持不变,纵坐标变为原来的一半,求所的曲线的方程,并说明它是什么曲线?
作 业 下课啦!同学们再相会!感谢各位领导和老师们的指导,
请多提宝贵意见!Class is over,
Thank you for your cooperation,goodbye
于常数(大于F1F2)的点的轨迹叫做椭圆,两
个定点F1、F2叫做椭圆的焦点,两焦点的距
离叫做椭圆的焦距.则:即: (a2-c2)x2+a2y2=a2(a2-c2)xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足PF1+PF2
为定值,设为2a,则2a>2c则:即:O标准方程的推导b2x2+a2y2=a2b2根据已知条件,求下列椭圆的焦点坐标 想一想(1)(2)想一想求适合下列条件的椭圆的标准方程(2) a=4, b=3解:∵焦点在y轴上∴设椭圆的标准方程为∵b=1, c= b2=a2-c2∴a2=b2+c2 即a2=16或例 : 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆,
它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为
3m,求这个椭圆的标准方程.解:以两焦点F1、F2所在直线为x轴,线段F1F2的垂直平分线为
y 轴,建立如图所示的直角坐标系xOy,则这个椭圆的标准
方程可设为根据题意有即因此,这个椭圆的标准方程为练 习 两个焦点分别是 (-2,0), (2,0),
且过点P求适合下列条件的椭圆的标准方程:法一: c=2法二: c=2 设椭圆标准方程为:2a=P +P 解:例 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?设所的曲线上任一点的坐标为(x,y),圆 =4上的对应点的坐标为(x’,y’),由题意可得:因为 =4所以即1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹根据所学知识完成下表a2-c2=b2课后研学 研究 (1) 根据椭圆标准方程你能说出它的其它性质吗? 如:椭圆的范围及a,b具有什么几何特征? (2)将圆x2+y2 = 4上的点的横坐标保持不变,纵坐标变为原来的一半,求所的曲线的方程,并说明它是什么曲线?
作 业 下课啦!同学们再相会!感谢各位领导和老师们的指导,
请多提宝贵意见!Class is over,
Thank you for your cooperation,goodbye
