椭圆标准方程(1)[下学期]
图片预览





文档简介
(共12张PPT)
椭圆的标准方程
执教:邳州市东方学校 陈磊
苏教版高中数学选修2-1
2006年8月24日,在捷克首都布拉格举行的国际天文学联合会大会通过行星的新定义,冥王星终于“惨遭降级”,被驱逐出了行星家族,被列为“矮行星”.
椭圆定义:
平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆.
其中两个定点F1,F2叫做椭圆的焦点;
两焦点间的距离叫做椭圆的焦距.
知识链接:
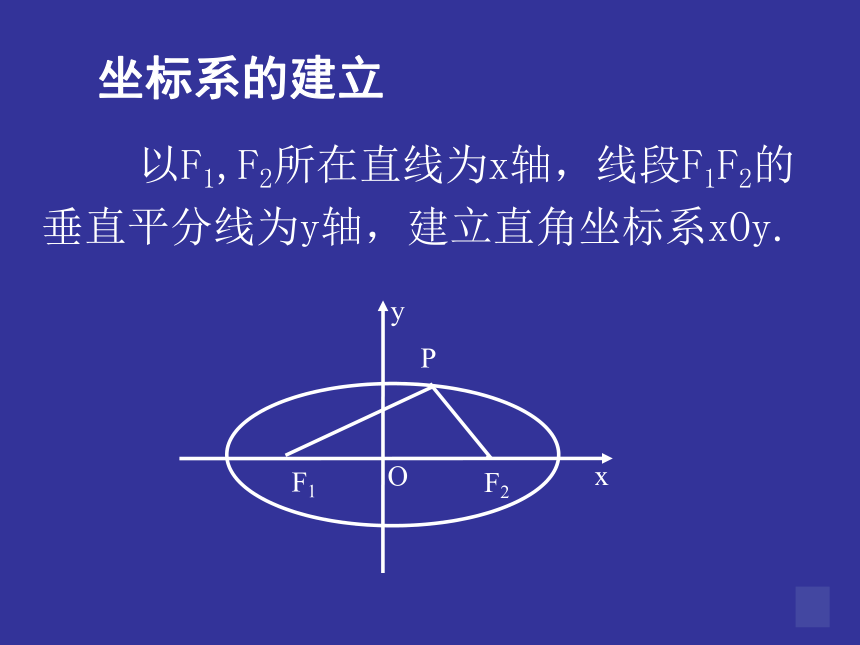
坐标系的建立
以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy.
O
y
x
P
F1
.
F2
设P(x,y)为椭圆上任意一点,
则PF1+PF2=2a.
O
P
y
F2
F1
x
F1F2=2c,
椭圆上任意一点P到F1,F2距离之和为常数2a(2a>2c),
则F1(-c,0)、F2 (c,0).
y
P (x, y)
O
F2(0, c)
F1(0, -c)
x
例题分析:
例1.已知一个运油车上的贮油罐横截面的 外轮廓线是一个椭圆,它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为3m, 求这个椭圆的标准方程.
P
F2
F1
O
y
x
练习:求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5.
答案:
(1)a= ,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
例2.求下列椭圆的焦点坐标.
问题:已知椭圆的标准方程,如何判断焦点所在的坐标轴?
焦点在分母大的那个轴上
(1)
(2) 16x2+7y2=112.
答案:(1)(-4,0),(4,0);
(2)(0, -3),(0,3).
已知方程 表示焦点在x轴
上的椭圆,则m的取值范围是 .
(0,4)
变式:已知方程 表示焦点在y轴上的椭圆,则m的取值范 围是 .
(1,2)
练习:
回顾反思
(1)椭圆标准方程的两种形式;
(2)椭圆标准方程焦点位置的判断方法;
(3)求椭圆标准方程的方法主要是利用待定系数法:先判断出焦点所在的位置,再求出a和b.
(4)体会观察、类比、数形结合等思想方法在数学中的应用.
课外作业:
教材第28页习题2.2(1):
第1(1)(4),2(3)(4),4题.
谢谢老师们、同学们!
再 见
椭圆的标准方程
执教:邳州市东方学校 陈磊
苏教版高中数学选修2-1
2006年8月24日,在捷克首都布拉格举行的国际天文学联合会大会通过行星的新定义,冥王星终于“惨遭降级”,被驱逐出了行星家族,被列为“矮行星”.
椭圆定义:
平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆.
其中两个定点F1,F2叫做椭圆的焦点;
两焦点间的距离叫做椭圆的焦距.
知识链接:
坐标系的建立
以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy.
O
y
x
P
F1
.
F2
设P(x,y)为椭圆上任意一点,
则PF1+PF2=2a.
O
P
y
F2
F1
x
F1F2=2c,
椭圆上任意一点P到F1,F2距离之和为常数2a(2a>2c),
则F1(-c,0)、F2 (c,0).
y
P (x, y)
O
F2(0, c)
F1(0, -c)
x
例题分析:
例1.已知一个运油车上的贮油罐横截面的 外轮廓线是一个椭圆,它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为3m, 求这个椭圆的标准方程.
P
F2
F1
O
y
x
练习:求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5.
答案:
(1)a= ,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
例2.求下列椭圆的焦点坐标.
问题:已知椭圆的标准方程,如何判断焦点所在的坐标轴?
焦点在分母大的那个轴上
(1)
(2) 16x2+7y2=112.
答案:(1)(-4,0),(4,0);
(2)(0, -3),(0,3).
已知方程 表示焦点在x轴
上的椭圆,则m的取值范围是 .
(0,4)
变式:已知方程 表示焦点在y轴上的椭圆,则m的取值范 围是 .
(1,2)
练习:
回顾反思
(1)椭圆标准方程的两种形式;
(2)椭圆标准方程焦点位置的判断方法;
(3)求椭圆标准方程的方法主要是利用待定系数法:先判断出焦点所在的位置,再求出a和b.
(4)体会观察、类比、数形结合等思想方法在数学中的应用.
课外作业:
教材第28页习题2.2(1):
第1(1)(4),2(3)(4),4题.
谢谢老师们、同学们!
再 见
