椭圆标准方程(5)[下学期]
图片预览





文档简介
课件22张PPT。椭圆的标准方程江苏省丹阳高级中学 丁玲普通高中课程标准实验教科书《数学》(选修2—1)教学目标:1.掌握椭圆的标准方程,能根据已知条件求
椭圆的标准方程。
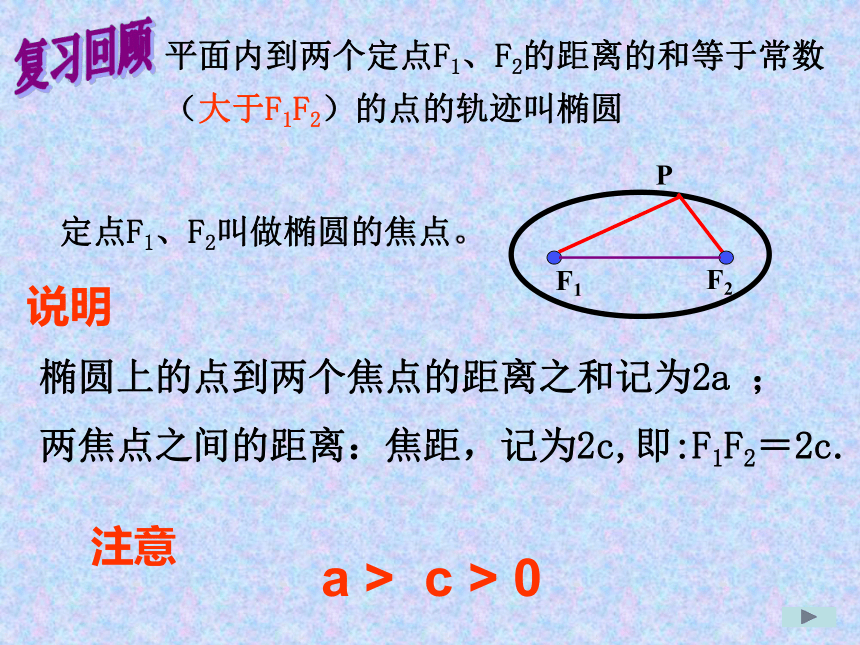
2.能用标准方程判定曲线是否是椭圆。复习回顾平面内到两个定点F1、F2的距离的和等于常数
(大于F1F2)的点的轨迹叫椭圆定点F1、F2叫做椭圆的焦点。F1F2P椭圆上的点到两个焦点的距离之和记为2a ;
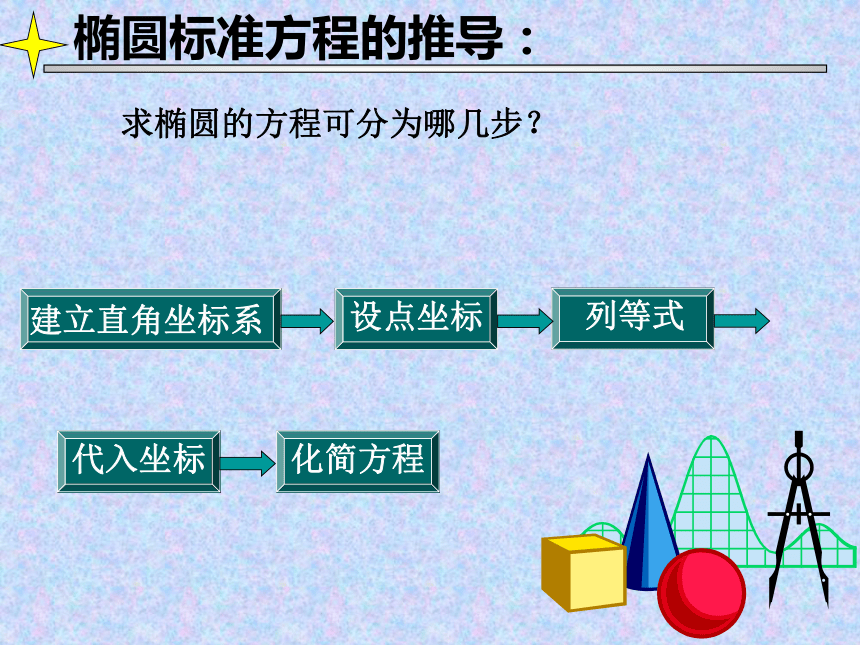
两焦点之间的距离:焦距,记为2c,即:F1F2=2c.说明注意a > c > 0椭圆标准方程的推导:求椭圆的方程可分为哪几步?如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线
作为坐标轴。)以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。F1F2 = 2c设P(x,y)为椭圆上的任意一点,∵F1F2=2c(c>0),则:F1(-c,0)、F2(c,0)以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。方程的推导方程的推导以直线F1F2为y轴,线段F1F2的垂直平分线为x轴,建立坐标系。方程的推导建立如图坐标系。设P(x,y)为椭圆上的任意一点,椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)1、已知椭圆的方程为:
则a=____,b=____,c=___, 焦点
坐标为:___ ,焦距等
于____。该椭圆上一点P到焦点F1的距
离为8,则点P到另一个焦点F2的距离
等于______。1068(0,-8)、(0,8)1612练习2、若椭圆满足: a=5 , c=3 ,
求它的标准方程。
焦点在x轴上时:焦点在y轴上时:焦点在x轴上B例题讲解解:以两个焦点F1,F2所在的直线为x轴,以线段F1F2的垂直平分线为y轴,建立直角坐标系,则这个椭圆的标准方程为根据题意知,2a=3,2c=2.4,即a=1.5,c=1.2。所以b2=a2-c2=1.52-1.22=0.81,因此椭圆的标准方程为例2、将圆x2+y2=4上的点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什么曲线因为x′2+y′2=4,所以x2+4y2=4,即这就是变换后所得曲线的方程,它表示一个椭圆小 结定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系{P|PF1+PF2=2a,2a>F1F2}思考题怎样判断焦点在哪个轴上?m>0,n>0,当n > m > 0时,焦点在y轴上当m > n > 0时,焦点在x轴上且m≠n作业1、教材P26页习题2.2(1)第2,3,4题2、推导:(用分子有理化)
焦点在y轴上的椭圆的标准方程
椭圆的标准方程。
2.能用标准方程判定曲线是否是椭圆。复习回顾平面内到两个定点F1、F2的距离的和等于常数
(大于F1F2)的点的轨迹叫椭圆定点F1、F2叫做椭圆的焦点。F1F2P椭圆上的点到两个焦点的距离之和记为2a ;
两焦点之间的距离:焦距,记为2c,即:F1F2=2c.说明注意a > c > 0椭圆标准方程的推导:求椭圆的方程可分为哪几步?如何建立适当的直角坐标系?原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线
作为坐标轴。)以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。F1F2 = 2c设P(x,y)为椭圆上的任意一点,∵F1F2=2c(c>0),则:F1(-c,0)、F2(c,0)以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。方程的推导方程的推导以直线F1F2为y轴,线段F1F2的垂直平分线为x轴,建立坐标系。方程的推导建立如图坐标系。设P(x,y)为椭圆上的任意一点,椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)1、已知椭圆的方程为:
则a=____,b=____,c=___, 焦点
坐标为:___ ,焦距等
于____。该椭圆上一点P到焦点F1的距
离为8,则点P到另一个焦点F2的距离
等于______。1068(0,-8)、(0,8)1612练习2、若椭圆满足: a=5 , c=3 ,
求它的标准方程。
焦点在x轴上时:焦点在y轴上时:焦点在x轴上B例题讲解解:以两个焦点F1,F2所在的直线为x轴,以线段F1F2的垂直平分线为y轴,建立直角坐标系,则这个椭圆的标准方程为根据题意知,2a=3,2c=2.4,即a=1.5,c=1.2。所以b2=a2-c2=1.52-1.22=0.81,因此椭圆的标准方程为例2、将圆x2+y2=4上的点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什么曲线因为x′2+y′2=4,所以x2+4y2=4,即这就是变换后所得曲线的方程,它表示一个椭圆小 结定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系{P|PF1+PF2=2a,2a>F1F2}思考题怎样判断焦点在哪个轴上?m>0,n>0,当n > m > 0时,焦点在y轴上当m > n > 0时,焦点在x轴上且m≠n作业1、教材P26页习题2.2(1)第2,3,4题2、推导:(用分子有理化)
焦点在y轴上的椭圆的标准方程
