椭圆标准方程（6）[下学期]

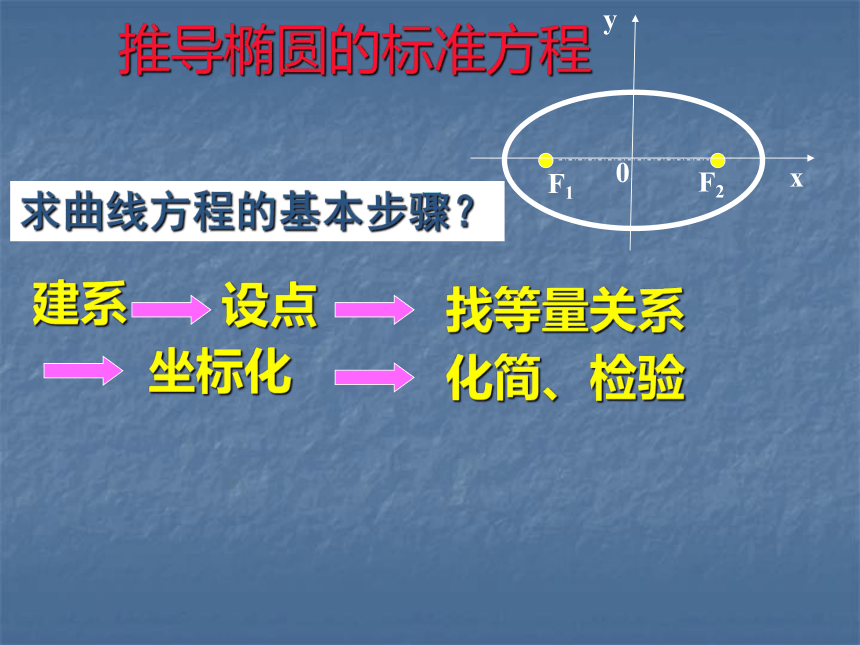
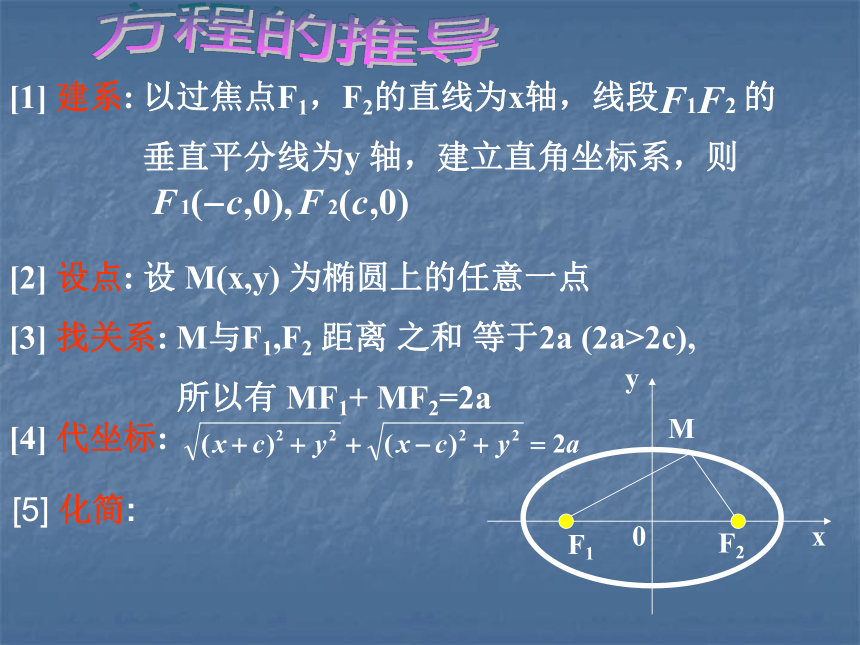
课件20张PPT。江苏省邗江中学　杨建萍椭圆动画演示问题情境生活中的应用 椭圆的标准方程生活中有椭圆,生活中用椭圆求曲线方程的基本步骤？设点建系找等量关系坐标化化简、检验推导椭圆的标准方程[1] 建系: 以过焦点F1，F2的直线为x轴，线段 的
垂直平分线为y 轴，建立直角坐标系，则
[2] 设点: 设 M(x,y) 为椭圆上的任意一点
[3] 找关系: M与F1,F2 距离 之和 等于2a (2a>2c),
　　　　　所以有 MF1+ MF2=2a
[4] 代坐标:方程的推导[5] 化简:∴∴∴令∴则，椭圆的方程为：方程的推导求曲线方程的基本步骤？设点建系找等量关系坐标化化简、检验推导椭圆的标准方程F1F2椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)
1、填空：
(1)已知椭圆的方程为 ，则a=___， b=___，c=____，焦点坐标为____________543(3,0)、(-3,0)(2)已知椭圆的方程为 ，则a=_____，b=_______，c=_______，焦点坐标为___________21(0,-1)、(0,1)巩固性练习
2、说出适合下列条件的椭圆标准方程
（1）　　　　　，焦点在x 轴上；
（2） 　 ，焦点在y 轴上。
巩固性练习例1、将圆　　　　　上的点的横坐标保持不变，纵坐标变为原来的一半，求所得的曲线的方程，并说明它是什么曲线。椭圆标准方程的应用解:设所得曲线上任一点
坐标为P(x,y),圆上的
对应点的坐标P’(x’,y’),由题意可得：
因为所以即这就是变换后所得曲线的方程，它表示一个椭圆。例2：已知一个运油车上的贮油罐横截面的外轮廓线是一个椭圆，它的焦距为2.4m，外轮廓线上的点到两个焦点距离的和为3m，求这个椭圆的标准方程。
解：以两焦点　　　所在直线为X轴，线段 　　的垂直平分线为y轴,建立平面直角坐标系xOy。
则这个椭圆的标准方程为:根据题意:2a=3,2c=2.4,所以：b2=1.52-1.22=0.81因此，这个椭圆的方程为：2. 标准方程的简单应用1.两类方程（焦点分别在x轴,y轴上的标准方程）　一种方法（待定系数系法）
两种思想（数形结合、分类讨论）
回顾反思F1(-c,0)，F2(c,0)F1(0,-c)，F2(0,c) 看分母的大小,焦点在分母大的那一项对应的坐标轴上.
1、 课本第28页习题1,2
2、课本第28页习题5

布置作业谢谢！