人教版九年级上册数学22.3实际问题与二次函数同步训练(Word版含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数同步训练(Word版含答案) | 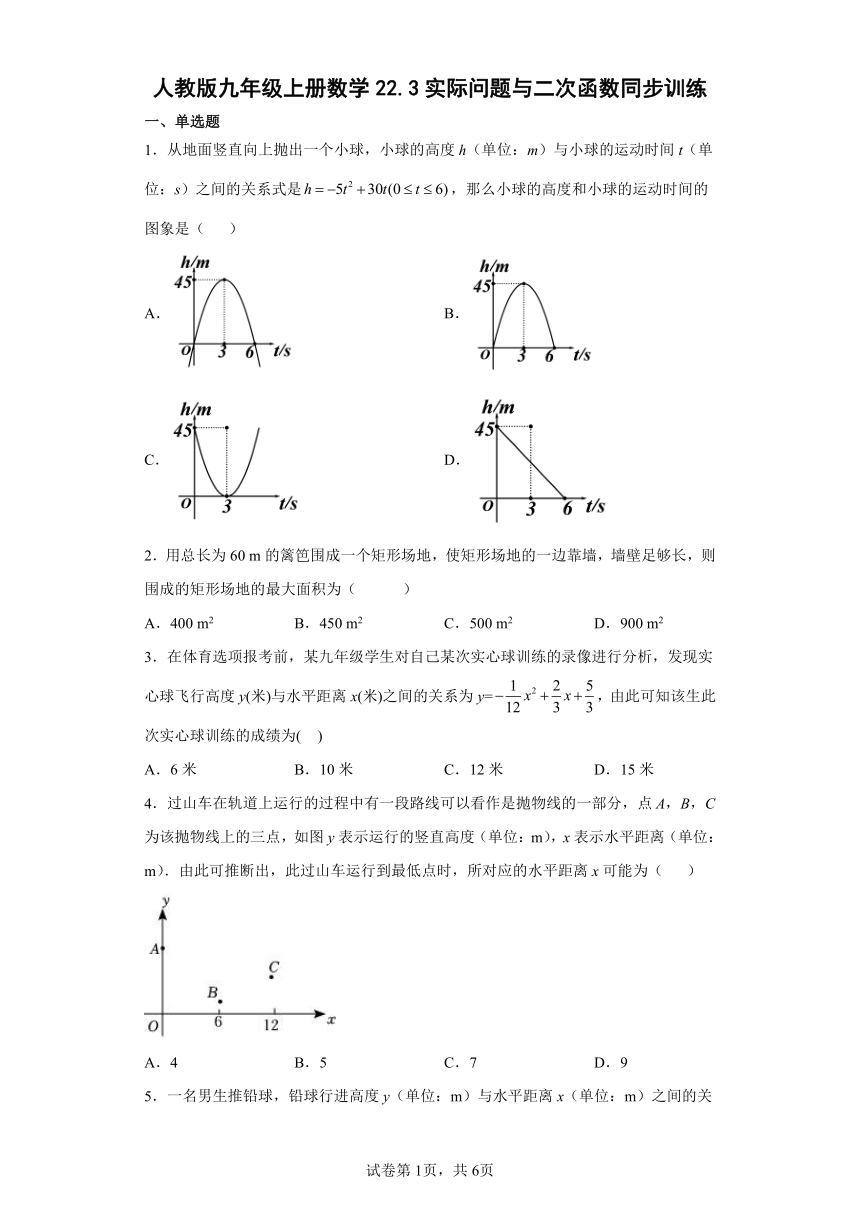 | |
| 格式 | docx | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 10:54:54 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与二次函数同步训练
一、单选题
1.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是( )
A. B.
C. D.
2.用总长为60 m的篱笆围成一个矩形场地,使矩形场地的一边靠墙,墙壁足够长,则围成的矩形场地的最大面积为( )
A.400 m2 B.450 m2 C.500 m2 D.900 m2
3.在体育选项报考前,某九年级学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
4.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
5.一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则他将铅球推出的距离为( )
A.m B.10m C.2m D.12m
6.在2021年山西省羽毛球锦标赛暨第十六届省运会羽毛球比赛中,某次羽毛球的运动路线可以看成是抛物线的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A. B.
C. D.
7.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
8.如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A. B.
C. D.
二、填空题
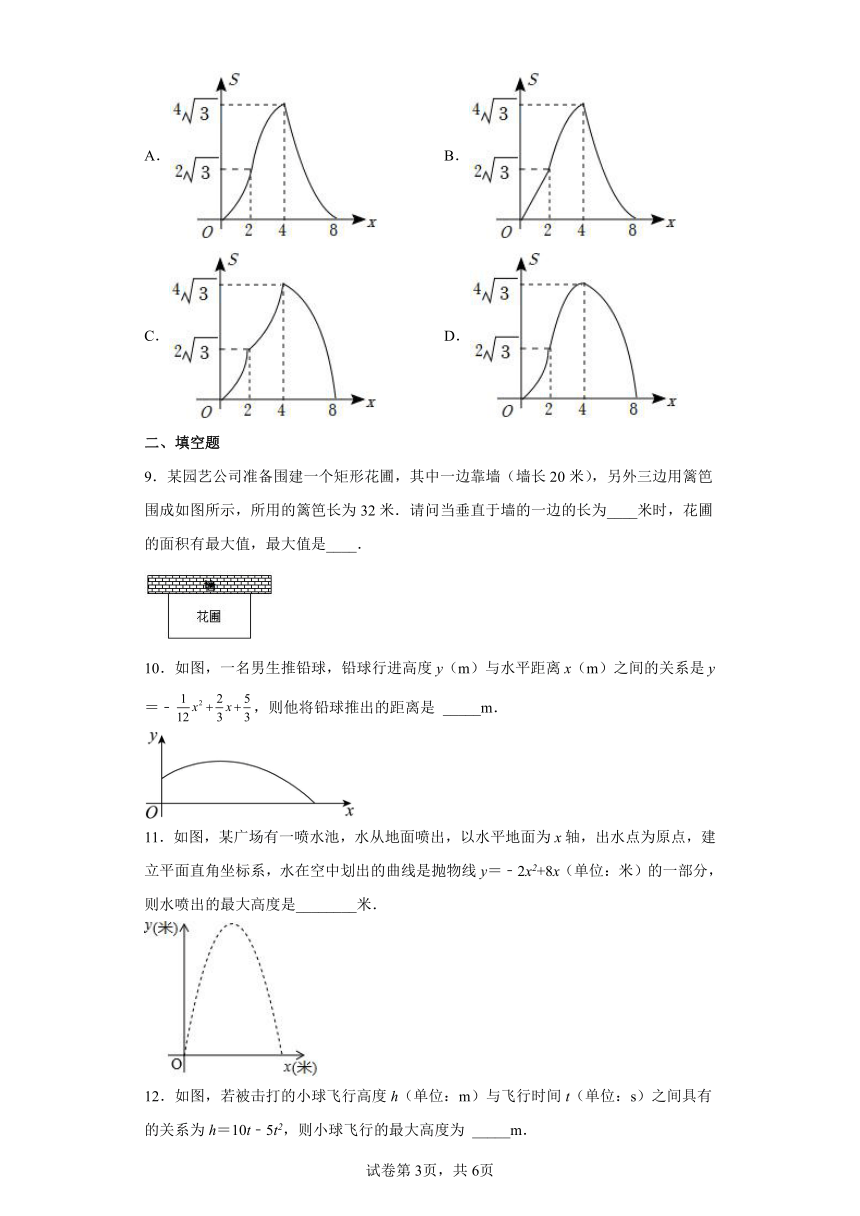
9.某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为32米.请问当垂直于墙的一边的长为____米时,花圃的面积有最大值,最大值是____.
10.如图,一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则他将铅球推出的距离是 _____m.
11.如图,某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣2x2+8x(单位:米)的一部分,则水喷出的最大高度是________米.
12.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)之间具有的关系为h=10t﹣5t2,则小球飞行的最大高度为 _____m.
13.某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为________.
14.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
15.如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
16.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
三、解答题
17.如图,某居民小区要在一块一边靠墙(墙长15 m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40 m的栅栏围成,设花园的边BC长为x m,花园的面积为y m2
(1)求y与x的函数解析式;
(2)满足条件的花园的面积能达到200 m2吗?若能,求出此时x的值;若不能,说明理由.
18.某店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映;调整价格时,售价每涨1元每月要少卖10件,售价每下降1元每月要多卖20件,为了获得更大的利润,现将商品售价调整为60+x(元/件)(即售价上涨,即售价下降),每月商品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?求最大月利润?
(3)为了使每月利润不少于6000元应如何控制销售价格?
19.某商场销售一种进价为30元/个的商品,当销售价格x(元/个)满足40<x<80时,其销售量y(万个)与x之间的关系式为y=﹣x+9.同时销售过程中的其它开支为50万元.
(1)求出商场销售这种商品的净利润z(万元)与销售价格x函数解析式,销售价格x定为多少时净利润最大,最大净利润是多少?
(2)若净利润预期不低于17.5万元,试求出销售价格x的取值范围;若还需考虑销售量尽可能大,销售价格x应定为多少元?
20.2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)求每月的销售量y(件)与销售单价x(元)之间的函数关系式.
(2)若销售单价为80元,则经销商每月获得的利润为多少元?
(3)设每月获得的利润为W(元),若想在不亏本的情况下,且获利不得高于70%,那么销售单价定为多少元时,销售这款文化衫每月所获得的利润最大?并求出最大利润.
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.B
2.B
3.B
4.C
5.B
6.A
7.C
8.A
9. 8 128平方米
10.10
11.8
12.5
13.或
14.
15.10
16.8
17.(1)
(2)不能,
18.(1)
(2)售价为65元时,月利润最大,最大月利润为6250元
(3)将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元
19.(1)z=﹣+12x﹣320,当x=60时,z最大,最大利润为40
(2)45≤x≤75,x=45时,销售量最大
20.(1)y=-10x+1000
(2)每月获得的利润为8000元
(3)销售单价为68元时,每月所获得的利润最大,为8960元.
答案第1页,共2页
答案第1页,共1页
一、单选题
1.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是( )
A. B.
C. D.
2.用总长为60 m的篱笆围成一个矩形场地,使矩形场地的一边靠墙,墙壁足够长,则围成的矩形场地的最大面积为( )
A.400 m2 B.450 m2 C.500 m2 D.900 m2
3.在体育选项报考前,某九年级学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
4.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
5.一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,则他将铅球推出的距离为( )
A.m B.10m C.2m D.12m
6.在2021年山西省羽毛球锦标赛暨第十六届省运会羽毛球比赛中,某次羽毛球的运动路线可以看成是抛物线的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A. B.
C. D.
7.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
8.如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A. B.
C. D.
二、填空题
9.某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为32米.请问当垂直于墙的一边的长为____米时,花圃的面积有最大值,最大值是____.
10.如图,一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则他将铅球推出的距离是 _____m.
11.如图,某广场有一喷水池,水从地面喷出,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣2x2+8x(单位:米)的一部分,则水喷出的最大高度是________米.
12.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)之间具有的关系为h=10t﹣5t2,则小球飞行的最大高度为 _____m.
13.某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为________.
14.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
15.如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
16.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
三、解答题
17.如图,某居民小区要在一块一边靠墙(墙长15 m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40 m的栅栏围成,设花园的边BC长为x m,花园的面积为y m2
(1)求y与x的函数解析式;
(2)满足条件的花园的面积能达到200 m2吗?若能,求出此时x的值;若不能,说明理由.
18.某店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映;调整价格时,售价每涨1元每月要少卖10件,售价每下降1元每月要多卖20件,为了获得更大的利润,现将商品售价调整为60+x(元/件)(即售价上涨,即售价下降),每月商品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?求最大月利润?
(3)为了使每月利润不少于6000元应如何控制销售价格?
19.某商场销售一种进价为30元/个的商品,当销售价格x(元/个)满足40<x<80时,其销售量y(万个)与x之间的关系式为y=﹣x+9.同时销售过程中的其它开支为50万元.
(1)求出商场销售这种商品的净利润z(万元)与销售价格x函数解析式,销售价格x定为多少时净利润最大,最大净利润是多少?
(2)若净利润预期不低于17.5万元,试求出销售价格x的取值范围;若还需考虑销售量尽可能大,销售价格x应定为多少元?
20.2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)求每月的销售量y(件)与销售单价x(元)之间的函数关系式.
(2)若销售单价为80元,则经销商每月获得的利润为多少元?
(3)设每月获得的利润为W(元),若想在不亏本的情况下,且获利不得高于70%,那么销售单价定为多少元时,销售这款文化衫每月所获得的利润最大?并求出最大利润.
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.B
2.B
3.B
4.C
5.B
6.A
7.C
8.A
9. 8 128平方米
10.10
11.8
12.5
13.或
14.
15.10
16.8
17.(1)
(2)不能,
18.(1)
(2)售价为65元时,月利润最大,最大月利润为6250元
(3)将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元
19.(1)z=﹣+12x﹣320,当x=60时,z最大,最大利润为40
(2)45≤x≤75,x=45时,销售量最大
20.(1)y=-10x+1000
(2)每月获得的利润为8000元
(3)销售单价为68元时,每月所获得的利润最大,为8960元.
答案第1页,共2页
答案第1页,共1页
同课章节目录
