椭圆的几何性质[上学期]
图片预览











文档简介
课件31张PPT。椭圆的几何性质复习一:椭圆的图形语言:焦三角形点P(x,y)与点P`(x,-y)复习二:点P与点P`的关系:点P(x,y)与点P`(-x,y)点P(x,y)与点P`(-x,-y)问题一:研究曲线的几何特征有什么意义? 研究曲线的几何性质可以从整体上把握曲线的形状.大小和位置. 怎样来研究曲线的几何
特征呢? 问题二:在解析几何里,是通过对曲线的方程的讨论来研究曲线的几何特征的 (a>b>0) 下面我们利用焦点在x轴上的
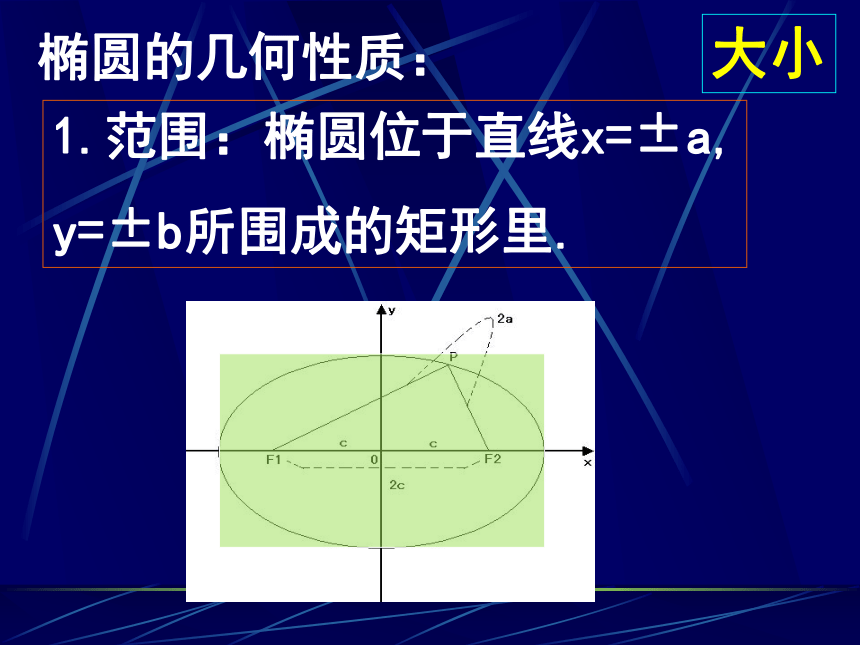
椭圆标准方程: 大小形状位置椭圆的几何性质:1.范围:椭圆位于直线x=±a,
y=±b所围成的矩形里. 大小椭圆的几何性质:2.对称性:
(1)以-y代y方程不变,关于x轴;
(2)以-x代x方程不变,关于y轴;
(3)同时以-y代y,-x代x
方程都不变,关于原点对称。形状标准方程表示椭圆,其中心是原点,对称轴是坐标轴,反过来,对称轴是坐标轴的椭圆,其中心是原点,其方程是标准方程位置椭圆的几何性质:(3)顶点:椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点。研究曲线上某些特殊点的位置,可以确定曲线的位置,要确定曲线在坐标系中的位置,常常需要求出特殊点的坐标,曲线与x轴、y轴的交点坐标. (4)长轴与短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴.它们的长分别是2a和2b ,其中a和b分别叫椭圆的长半轴长和短半轴长. a、b、c三者都有了几何意义,它们分别是长半轴长、短半轴长、半焦距.? 椭圆的几何性质:a、b、c的意义:abc4.离心率 椭圆的几何性质:椭圆的焦距与长轴长
的比 ,
叫做椭圆的离心率. <1>离心率e的范围: <2>离心率e的几何意义: 0<e<1 e越接近于1,椭圆就越扁;e越接近于0,椭圆就越接近于圆.例1:求下列椭圆的范围,对称轴方程,
顶点坐标,焦点坐标,长轴长,
短轴长,焦距,离心率。
(1)x2+4y2=4
(2)4x2+y2=16 画出椭圆的草图例2:求适合下列条件的椭圆的
标准方程。
(1)椭圆的两顶点为P(-3,0),
Q(0,-2),
(2)长轴长为20,离心率为例3:求下列条件的椭圆的离心率。
(1)连接椭圆的一个顶点与两个
焦点构成正三角形;
(2)椭圆的一个焦点将长轴分成
两段。练习: 小结
能掌握利用椭圆的标准方程
讨论椭圆的几何性质的方法,
掌握椭圆的几何性质。(±b,0),(0,±a)(± a,0)(0,±b)x轴短轴长2b,y轴长轴长2a0
特征呢? 问题二:在解析几何里,是通过对曲线的方程的讨论来研究曲线的几何特征的 (a>b>0) 下面我们利用焦点在x轴上的
椭圆标准方程: 大小形状位置椭圆的几何性质:1.范围:椭圆位于直线x=±a,
y=±b所围成的矩形里. 大小椭圆的几何性质:2.对称性:
(1)以-y代y方程不变,关于x轴;
(2)以-x代x方程不变,关于y轴;
(3)同时以-y代y,-x代x
方程都不变,关于原点对称。形状标准方程表示椭圆,其中心是原点,对称轴是坐标轴,反过来,对称轴是坐标轴的椭圆,其中心是原点,其方程是标准方程位置椭圆的几何性质:(3)顶点:椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点。研究曲线上某些特殊点的位置,可以确定曲线的位置,要确定曲线在坐标系中的位置,常常需要求出特殊点的坐标,曲线与x轴、y轴的交点坐标. (4)长轴与短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴.它们的长分别是2a和2b ,其中a和b分别叫椭圆的长半轴长和短半轴长. a、b、c三者都有了几何意义,它们分别是长半轴长、短半轴长、半焦距.? 椭圆的几何性质:a、b、c的意义:abc4.离心率 椭圆的几何性质:椭圆的焦距与长轴长
的比 ,
叫做椭圆的离心率. <1>离心率e的范围: <2>离心率e的几何意义: 0<e<1 e越接近于1,椭圆就越扁;e越接近于0,椭圆就越接近于圆.例1:求下列椭圆的范围,对称轴方程,
顶点坐标,焦点坐标,长轴长,
短轴长,焦距,离心率。
(1)x2+4y2=4
(2)4x2+y2=16 画出椭圆的草图例2:求适合下列条件的椭圆的
标准方程。
(1)椭圆的两顶点为P(-3,0),
Q(0,-2),
(2)长轴长为20,离心率为例3:求下列条件的椭圆的离心率。
(1)连接椭圆的一个顶点与两个
焦点构成正三角形;
(2)椭圆的一个焦点将长轴分成
两段。练习: 小结
能掌握利用椭圆的标准方程
讨论椭圆的几何性质的方法,
掌握椭圆的几何性质。(±b,0),(0,±a)(± a,0)(0,±b)x轴短轴长2b,y轴长轴长2a0
