甘肃省武威市第十八中学2021-2022学年高二下学期期中考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 甘肃省武威市第十八中学2021-2022学年高二下学期期中考试数学(理)试题(Word版含答案) | 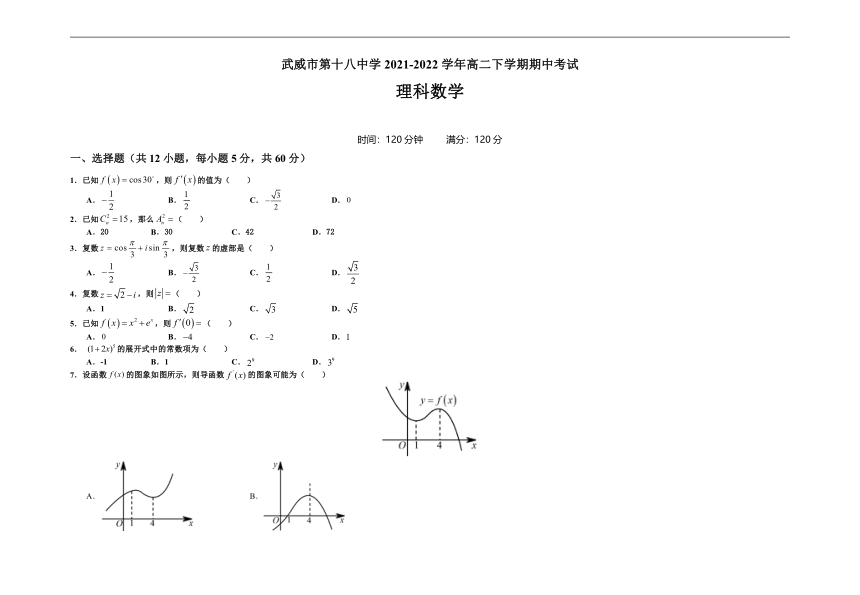 | |
| 格式 | docx | ||
| 文件大小 | 195.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 18:45:01 | ||
图片预览

文档简介
武威市第十八中学2021-2022学年高二下学期期中考试
理科数学
时间:120分钟 满分:120分
一、选择题(共12小题,每小题5分,共60分)
1.已知,则的值为( )
A. B. C. D.
2.已知,那么( )
A.20 B.30 C.42 D.72
3.复数,则复数的虚部是( )
A. B. C. D.
4.复数,则( )
A.1 B. C. D.
5.已知,则( )
A. B. C. D.
6. 的展开式中的常数项为( )
A.-1 B.1 C. D.
7.设函数的图象如图所示,则导函数的图象可能为( )
A. B.
C. D.
8.函数的极大值点为( )
A.1 B.-1 C.(1,-1) D.(-1,1)
9.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在新冠肺炎疫情防控期间,某记者要去武汉4个方舱医院采访,则不同的采访顺序有( )
A.4种 B.12种 C.18种 D.24种
11.曲线在点处的切线斜率为,则实数的值为( )
A. B.
C. D.
12.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
A.BD∥平面CB1D1 B.AC1⊥BD
C.AC1⊥平面CB1D1 D.异面直线AD与CB1所成的角为60°
二、填空题(共4小题,每小题5分,共20分)
13.若是虚数单位,则___________.
14.函数的导数为_____________.
15.若函数在处取得极值,则________.
16.某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有________种.
三、解答题(本大题共4小题,共40分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间.
18.(10分)已知二项式的展开式中共有6项.
(1)求展开式中所有二项式系数的和;
(2)求展开式中含的项.
19.(10分)已知函数在处取得极值7.
(1)求的值;
(2)求函数在区间上的最大值
20.(10分)从某小组的5名女生和4名男生中任选3人去参加一项公益活动.
(1) 求所选3人中恰有一名男生的概率;
(2) 求所选3人中男生人数ξ的分布列.
高二数学(理科)
一、选择题
1-5 DBDCD 2-10 BCAAD 11-12 BD
二、填空题
13. -1+2i 14. 15. 3 16. 16
17.
(1);(2)函数的单调增区间为,,单调减区间为.
【解析】(1)由,得,所以,
又,所以曲线在点处的切线方程为,
即.
(2)令,得,、、在上的情况如下:
递增 极大值 递减 极小值 递增
所以函数的单调增区间为,,单调减区间为
18.
(1)32;(2).
(1)由于二项展开式有6项,故. 所有二项式的系数和为.
(2)二项式展开式的通项为,令得. 故展开式中含的项为.
19.
(1);(2).
【解析】(1)因为,所以,
又函数在处取得极值7,
,解得;所以,
由得或;由得;满足题意;
(2)又, 由(1)得在上单调递增,在上单调递减,
因此.
20. (1) 所选3人中恰有一名男生的概率;
(2) 的可能取值为0,1,2,3.
∴ξ的分布列为:
0 1 2 3
理科数学
时间:120分钟 满分:120分
一、选择题(共12小题,每小题5分,共60分)
1.已知,则的值为( )
A. B. C. D.
2.已知,那么( )
A.20 B.30 C.42 D.72
3.复数,则复数的虚部是( )
A. B. C. D.
4.复数,则( )
A.1 B. C. D.
5.已知,则( )
A. B. C. D.
6. 的展开式中的常数项为( )
A.-1 B.1 C. D.
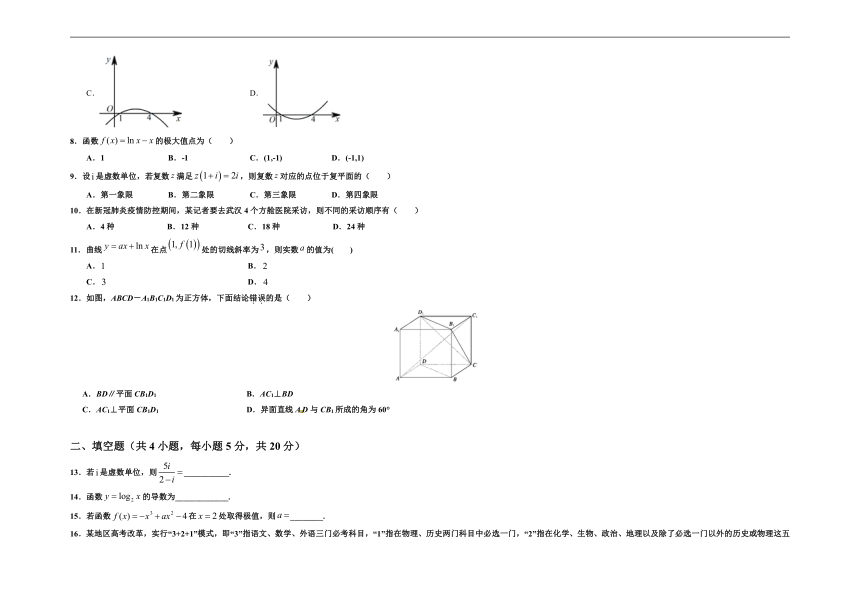
7.设函数的图象如图所示,则导函数的图象可能为( )
A. B.
C. D.
8.函数的极大值点为( )
A.1 B.-1 C.(1,-1) D.(-1,1)
9.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在新冠肺炎疫情防控期间,某记者要去武汉4个方舱医院采访,则不同的采访顺序有( )
A.4种 B.12种 C.18种 D.24种
11.曲线在点处的切线斜率为,则实数的值为( )
A. B.
C. D.
12.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
A.BD∥平面CB1D1 B.AC1⊥BD
C.AC1⊥平面CB1D1 D.异面直线AD与CB1所成的角为60°
二、填空题(共4小题,每小题5分,共20分)
13.若是虚数单位,则___________.
14.函数的导数为_____________.
15.若函数在处取得极值,则________.
16.某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有________种.
三、解答题(本大题共4小题,共40分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间.
18.(10分)已知二项式的展开式中共有6项.
(1)求展开式中所有二项式系数的和;
(2)求展开式中含的项.
19.(10分)已知函数在处取得极值7.
(1)求的值;
(2)求函数在区间上的最大值
20.(10分)从某小组的5名女生和4名男生中任选3人去参加一项公益活动.
(1) 求所选3人中恰有一名男生的概率;
(2) 求所选3人中男生人数ξ的分布列.
高二数学(理科)
一、选择题
1-5 DBDCD 2-10 BCAAD 11-12 BD
二、填空题
13. -1+2i 14. 15. 3 16. 16
17.
(1);(2)函数的单调增区间为,,单调减区间为.
【解析】(1)由,得,所以,
又,所以曲线在点处的切线方程为,
即.
(2)令,得,、、在上的情况如下:
递增 极大值 递减 极小值 递增
所以函数的单调增区间为,,单调减区间为
18.
(1)32;(2).
(1)由于二项展开式有6项,故. 所有二项式的系数和为.
(2)二项式展开式的通项为,令得. 故展开式中含的项为.
19.
(1);(2).
【解析】(1)因为,所以,
又函数在处取得极值7,
,解得;所以,
由得或;由得;满足题意;
(2)又, 由(1)得在上单调递增,在上单调递减,
因此.
20. (1) 所选3人中恰有一名男生的概率;
(2) 的可能取值为0,1,2,3.
∴ξ的分布列为:
0 1 2 3
同课章节目录
