甘肃省武威市第十八中学2021-2022学年高二下学期期中考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 甘肃省武威市第十八中学2021-2022学年高二下学期期中考试数学(文)试题(Word版含答案) | 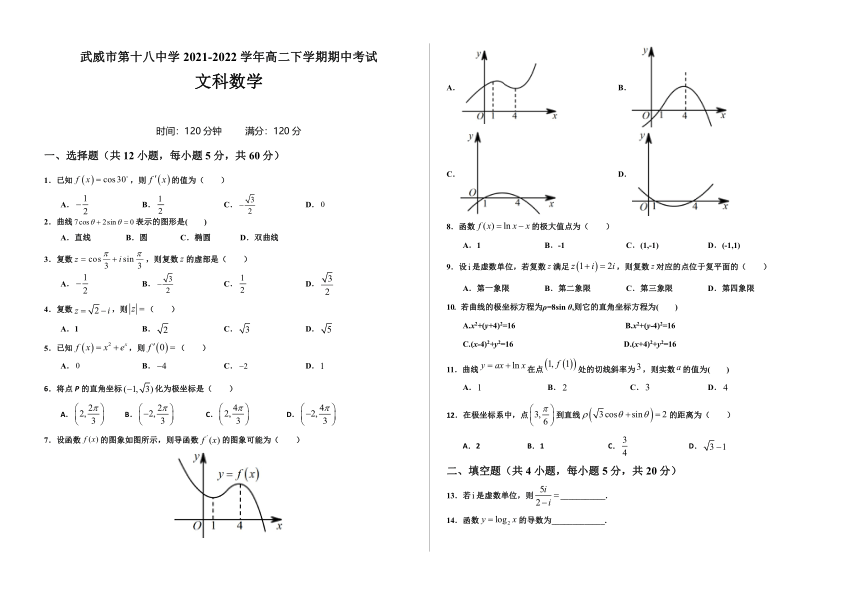 | |
| 格式 | docx | ||
| 文件大小 | 214.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 18:45:52 | ||
图片预览


文档简介
武威市第十八中学2021-2022学年高二下学期期中考试
文科数学
时间:120分钟 满分:120分
一、选择题(共12小题,每小题5分,共60分)
1.已知,则的值为( )
A. B. C. D.
2.曲线表示的图形是( )
A.直线 B.圆 C.椭圆 D.双曲线
3.复数,则复数的虚部是( )
A. B. C. D.
4.复数,则( )
A.1 B. C. D.
5.已知,则( )
A. B. C. D.
6.将点P的直角坐标化为极坐标是( )
A. B. C. D.
7.设函数的图象如图所示,则导函数的图象可能为( )
A. B.
C. D.
8.函数的极大值点为( )
A.1 B.-1 C.(1,-1) D.(-1,1)
9.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10. 若曲线的极坐标方程为ρ=8sin θ,则它的直角坐标方程为( )
A.x2+(y+4)2=16 B.x2+(y-4)2=16
C.(x-4)2+y2=16 D.(x+4)2+y2=16
11.曲线在点处的切线斜率为,则实数的值为( )
A. B. C. D.
12.在极坐标系中,点到直线的距离为( )
A.2 B.1 C. D.
二、填空题(共4小题,每小题5分,共20分)
13.若是虚数单位,则___________.
14.函数的导数为_____________.
15.若函数在处取得极值,则________.
16.若椭圆的参数方程为(为参数),则该椭圆的离心率为________.
三、解答题(本大题共4小题,共40分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间.
18.(10分)为了解决消费者在网购退货过程中和商家由于运费问题产生的纠纷,某保险公司推出退货“运费险”.消费者在购买商品时可选择是否购买运费险.当购买运费险的消费者退货时,保险公司将按约定对消费者的退货运费进行赔付.该保险公司随机调查了100名消费者,统计数据如下:
不购买运费险 购买运费险 总计
农村消费者 40
城镇消费者 3
总计 10 100
(1)请将上面列联表补充完整,
(2)是否有95%的把握认为消费者购买运费险与城镇农村有关?
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
19.(10分)已知函数在处取得极值7.
(1)求的值;
(2)求函数在区间上的最大值
20.(10分)在直角坐标系 中,直线的参数方程为(为参数),以坐标原点 为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)写出直线的普通方程与曲线的直角坐标方程;
(2)求直线被曲线截得的弦长.
高二数学(文科)答案
一、选择题
1-5 DADCD 2-10 ACAAB 11-12 BA
二、填空题
13. -1+2i 14. 15. 3 16.
17.
(1);(2)函数的单调增区间为,,单调减区间为.
(1)由,得,所以,
又,所以曲线在点处的切线方程为,
即.
(2)令,得,、、在上的情况如下:
递增 极大值 递减 极小值 递增
所以函数的单调增区间为,,单调减区间为
18.
(1)列联表如下:
不购买运费险 购买运费险 总计
农村消费者 7 33 40
城镇消费者 3 57 60
总计 10 90 100
(2),
所以有95%的把握认为消费者购买运费险与城镇农村有关.
19.
(1);(2).
(1)因为,所以,
又函数在处取得极值7,
,解得;所以,
由得或;由得;满足题意;
(2)又,
由(1)得在上单调递增,在上单调递减,
因此.
20.
(1),;(2).
(1)由直线的参数方程( t为参数可得其普通方程为:
;
由曲线的极坐标方程得,所以曲线的直角坐标方程为:
.
(2)由(1)得曲线:,圆心到直线的距离为:,
所以直线被曲线截得的弦长为:.
文科数学
时间:120分钟 满分:120分
一、选择题(共12小题,每小题5分,共60分)
1.已知,则的值为( )
A. B. C. D.
2.曲线表示的图形是( )
A.直线 B.圆 C.椭圆 D.双曲线
3.复数,则复数的虚部是( )
A. B. C. D.
4.复数,则( )
A.1 B. C. D.
5.已知,则( )
A. B. C. D.
6.将点P的直角坐标化为极坐标是( )
A. B. C. D.
7.设函数的图象如图所示,则导函数的图象可能为( )
A. B.
C. D.
8.函数的极大值点为( )
A.1 B.-1 C.(1,-1) D.(-1,1)
9.设是虚数单位,若复数满足,则复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10. 若曲线的极坐标方程为ρ=8sin θ,则它的直角坐标方程为( )
A.x2+(y+4)2=16 B.x2+(y-4)2=16
C.(x-4)2+y2=16 D.(x+4)2+y2=16
11.曲线在点处的切线斜率为,则实数的值为( )
A. B. C. D.
12.在极坐标系中,点到直线的距离为( )
A.2 B.1 C. D.
二、填空题(共4小题,每小题5分,共20分)
13.若是虚数单位,则___________.
14.函数的导数为_____________.
15.若函数在处取得极值,则________.
16.若椭圆的参数方程为(为参数),则该椭圆的离心率为________.
三、解答题(本大题共4小题,共40分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知函数.
(1)求曲线在点处的切线方程;
(2)求函数的单调区间.
18.(10分)为了解决消费者在网购退货过程中和商家由于运费问题产生的纠纷,某保险公司推出退货“运费险”.消费者在购买商品时可选择是否购买运费险.当购买运费险的消费者退货时,保险公司将按约定对消费者的退货运费进行赔付.该保险公司随机调查了100名消费者,统计数据如下:
不购买运费险 购买运费险 总计
农村消费者 40
城镇消费者 3
总计 10 100
(1)请将上面列联表补充完整,
(2)是否有95%的把握认为消费者购买运费险与城镇农村有关?
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
19.(10分)已知函数在处取得极值7.
(1)求的值;
(2)求函数在区间上的最大值
20.(10分)在直角坐标系 中,直线的参数方程为(为参数),以坐标原点 为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)写出直线的普通方程与曲线的直角坐标方程;
(2)求直线被曲线截得的弦长.
高二数学(文科)答案
一、选择题
1-5 DADCD 2-10 ACAAB 11-12 BA
二、填空题
13. -1+2i 14. 15. 3 16.
17.
(1);(2)函数的单调增区间为,,单调减区间为.
(1)由,得,所以,
又,所以曲线在点处的切线方程为,
即.
(2)令,得,、、在上的情况如下:
递增 极大值 递减 极小值 递增
所以函数的单调增区间为,,单调减区间为
18.
(1)列联表如下:
不购买运费险 购买运费险 总计
农村消费者 7 33 40
城镇消费者 3 57 60
总计 10 90 100
(2),
所以有95%的把握认为消费者购买运费险与城镇农村有关.
19.
(1);(2).
(1)因为,所以,
又函数在处取得极值7,
,解得;所以,
由得或;由得;满足题意;
(2)又,
由(1)得在上单调递增,在上单调递减,
因此.
20.
(1),;(2).
(1)由直线的参数方程( t为参数可得其普通方程为:
;
由曲线的极坐标方程得,所以曲线的直角坐标方程为:
.
(2)由(1)得曲线:,圆心到直线的距离为:,
所以直线被曲线截得的弦长为:.
同课章节目录
