人教版八年级上册11.2.2三角形的外角课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.2三角形的外角课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 384.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.2三角形的外角
1. 理解并掌握三角形的外角的概念,并能够在复杂
图形中找出外角;
2. 掌握三角形的外角的性质和三角形外角和;(重点)
3. 会利用三角形的外角性质解决有关问题.(难点)
教学目标
新课引入
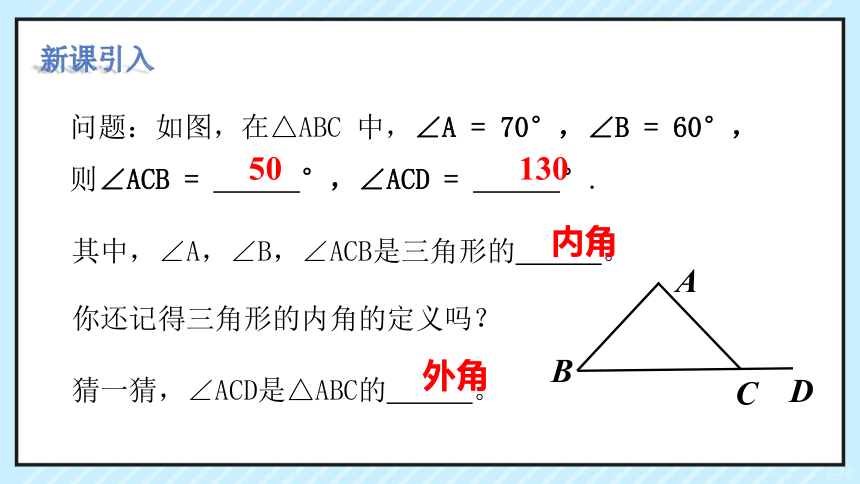
问题:如图,在△ABC 中,∠A = 70°,∠B = 60°,
则∠ACB = °,∠ACD = °.
A
B
C
D
50
130
其中,∠A,∠B,∠ACB是三角形的 。
你还记得三角形的内角的定义吗?
猜一猜,∠ACD是△ABC的 。
内角
外角
探究新知1
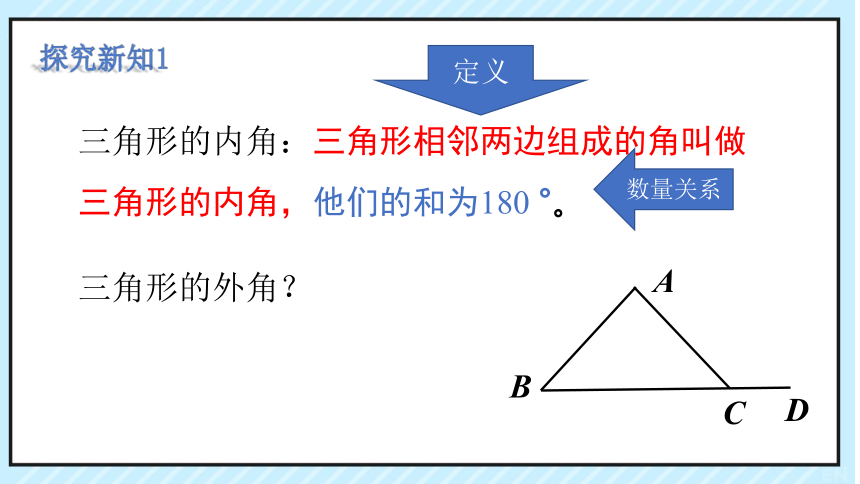
三角形的内角:三角形相邻两边组成的角叫做三角形的内角,他们的和为180 °。
三角形的外角?
定义
数量关系
A
B
C
D
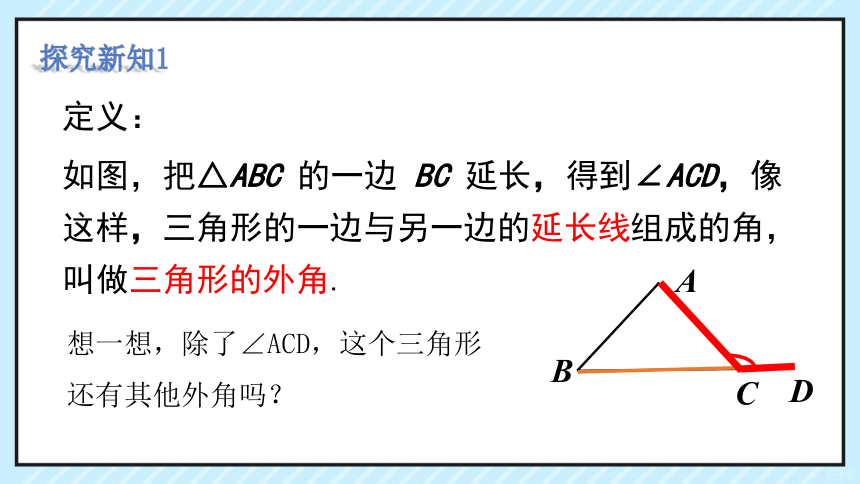
如图,把△ABC 的一边 BC 延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
探究新知1
A
B
C
D
定义:
想一想,除了∠ACD,这个三角形还有其他外角吗?
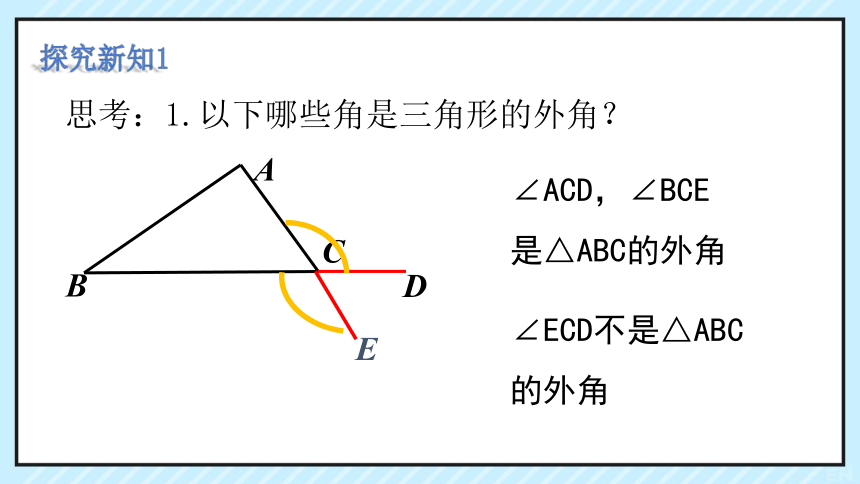
思考:1.以下哪些角是三角形的外角?
探究新知1
C
B
A
D
E
∠ACD,∠BCE
是△ABC的外角
∠ECD不是△ABC的外角
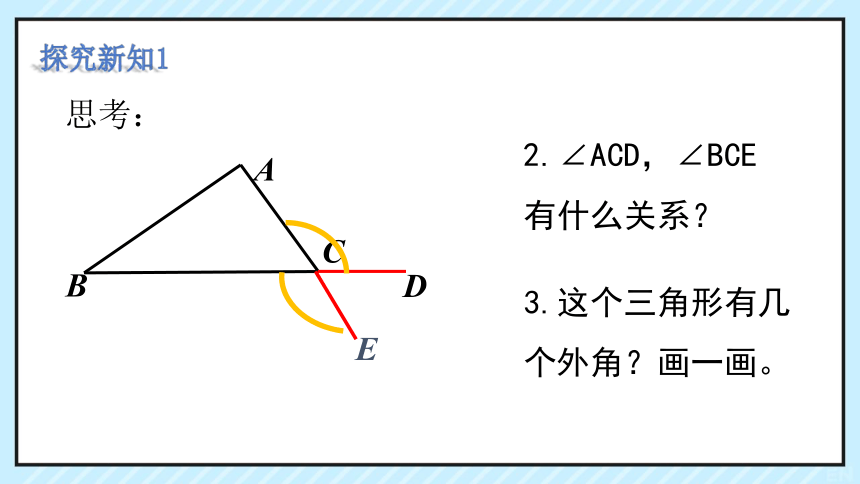
思考:
探究新知1
C
B
A
D
E
2.∠ACD,∠BCE
有什么关系?
3.这个三角形有几个外角?画一画。
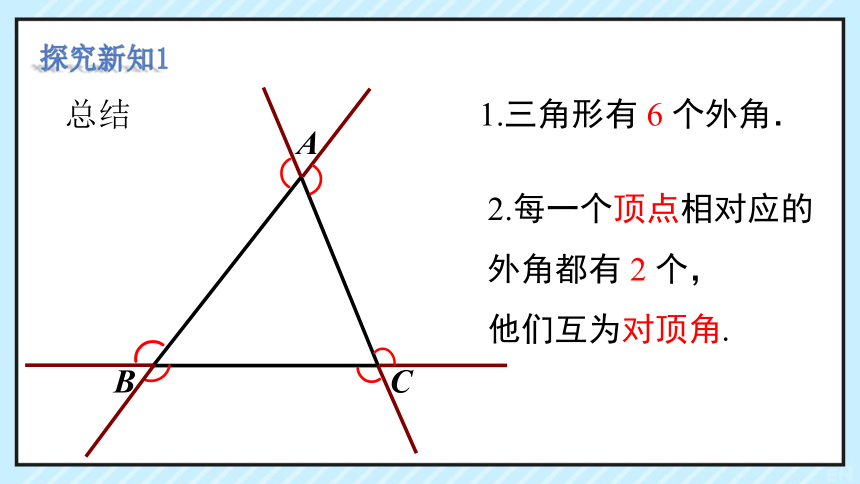
1.三角形有 6 个外角.
探究新知1
2.每一个顶点相对应的
外角都有 2 个,
他们互为对顶角.
A
B
C
总结
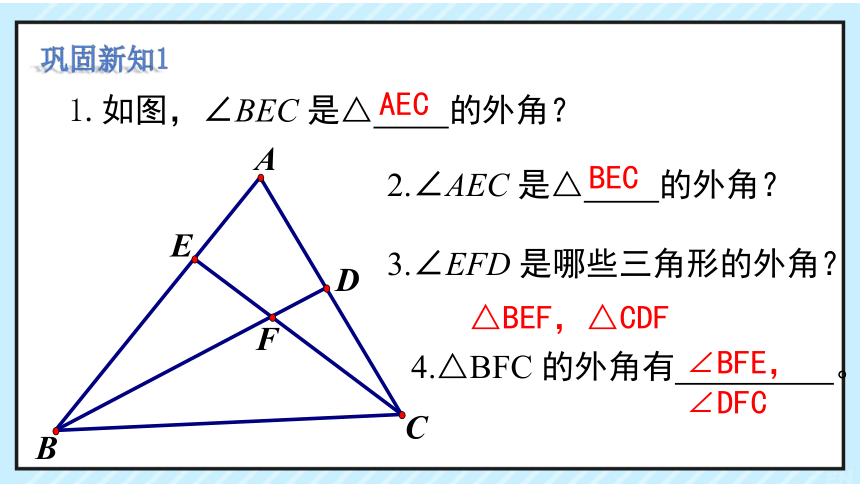
1.如图,∠BEC 是△ 的外角?
巩固新知1
F
B
C
D
E
A
2.∠AEC 是△ 的外角?
3.∠EFD 是哪些三角形的外角?
AEC
BEC
△BEF,△CDF
4.△BFC 的外角有 。
∠BFE,∠DFC
5.如图,你还能提出什么问题?
巩固新知1
F
B
C
D
E
A
巩固新知1
探究:∠A,∠B,∠ACB和∠ACD之间是否有数量关系?
A
B
C
D
∠ACB+∠ACD=180°
平角
∠A +∠B +∠ACB = 180°
∠ACD +∠ACB = 180°
∠A+∠B=∠ACD
巩固新知1
三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
数学语言:
∵∠ACD 是△ABC 的一个外角
∴∠ACD =∠A +∠B
巩固新知2
1.说出下列图形中∠1 和∠2 的度数:
A
B
C
D
(
(
(
80°
60°
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50°
32°
(2)
∠1 = °,∠2 = °
∠1 = °,∠2 = °
40
130
18
140
巩固新知2
2.如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,求∠BFC 的度数.
探究新知3
如图, ∠BAE, ∠CBF, ∠ACD 是△ABC 的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE + ∠CBF + ∠ACD=360°
三角形的外角和等于 360°
巩固新知3
1.如图,∠A +∠B +∠C +∠D +∠E +∠F = .
360°
课堂小结
三角形的外角(6个)
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于 360°
巩固练习
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和.( )
(2)三角形的外角和等于它的内角和的 2 倍. ( )
(3)三角形的一个外角等于两个内角的和. ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和.( )
(5)三角形的一个外角大于任何一个内角. ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
巩固练习
2.如图,AB∥CD,∠A=37°, ∠C=63°,那么
∠F 等于( )
A
A. 26°
B. 63°
C. 37°
D. 60°
F
A
B
E
C
D
巩固练习
3.如图,D 是△ABC 的 BC 边上一点,∠B = ∠BAD, ∠ADC = 80°,∠BAC = 70°,求:
(1)∠B 的度数;
(2)∠C 的度数.
A
B
C
D
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.2三角形的外角
1. 理解并掌握三角形的外角的概念,并能够在复杂
图形中找出外角;
2. 掌握三角形的外角的性质和三角形外角和;(重点)
3. 会利用三角形的外角性质解决有关问题.(难点)
教学目标
新课引入
问题:如图,在△ABC 中,∠A = 70°,∠B = 60°,
则∠ACB = °,∠ACD = °.
A
B
C
D
50
130
其中,∠A,∠B,∠ACB是三角形的 。
你还记得三角形的内角的定义吗?
猜一猜,∠ACD是△ABC的 。
内角
外角
探究新知1
三角形的内角:三角形相邻两边组成的角叫做三角形的内角,他们的和为180 °。
三角形的外角?
定义
数量关系
A
B
C
D
如图,把△ABC 的一边 BC 延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
探究新知1
A
B
C
D
定义:
想一想,除了∠ACD,这个三角形还有其他外角吗?
思考:1.以下哪些角是三角形的外角?
探究新知1
C
B
A
D
E
∠ACD,∠BCE
是△ABC的外角
∠ECD不是△ABC的外角
思考:
探究新知1
C
B
A
D
E
2.∠ACD,∠BCE
有什么关系?
3.这个三角形有几个外角?画一画。
1.三角形有 6 个外角.
探究新知1
2.每一个顶点相对应的
外角都有 2 个,
他们互为对顶角.
A
B
C
总结
1.如图,∠BEC 是△ 的外角?
巩固新知1
F
B
C
D
E
A
2.∠AEC 是△ 的外角?
3.∠EFD 是哪些三角形的外角?
AEC
BEC
△BEF,△CDF
4.△BFC 的外角有 。
∠BFE,∠DFC
5.如图,你还能提出什么问题?
巩固新知1
F
B
C
D
E
A
巩固新知1
探究:∠A,∠B,∠ACB和∠ACD之间是否有数量关系?
A
B
C
D
∠ACB+∠ACD=180°
平角
∠A +∠B +∠ACB = 180°
∠ACD +∠ACB = 180°
∠A+∠B=∠ACD
巩固新知1
三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
A
B
C
D
数学语言:
∵∠ACD 是△ABC 的一个外角
∴∠ACD =∠A +∠B
巩固新知2
1.说出下列图形中∠1 和∠2 的度数:
A
B
C
D
(
(
(
80°
60°
(
2
1
(1)
A
B
C
(
(
(
(
2
1
50°
32°
(2)
∠1 = °,∠2 = °
∠1 = °,∠2 = °
40
130
18
140
巩固新知2
2.如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,求∠BFC 的度数.
探究新知3
如图, ∠BAE, ∠CBF, ∠ACD 是△ABC 的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE + ∠CBF + ∠ACD=360°
三角形的外角和等于 360°
巩固新知3
1.如图,∠A +∠B +∠C +∠D +∠E +∠F = .
360°
课堂小结
三角形的外角(6个)
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于 360°
巩固练习
1.判断下列命题的对错.
(1)三角形的外角和是指三角形的所有外角的和.( )
(2)三角形的外角和等于它的内角和的 2 倍. ( )
(3)三角形的一个外角等于两个内角的和. ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和.( )
(5)三角形的一个外角大于任何一个内角. ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角.( )
巩固练习
2.如图,AB∥CD,∠A=37°, ∠C=63°,那么
∠F 等于( )
A
A. 26°
B. 63°
C. 37°
D. 60°
F
A
B
E
C
D
巩固练习
3.如图,D 是△ABC 的 BC 边上一点,∠B = ∠BAD, ∠ADC = 80°,∠BAC = 70°,求:
(1)∠B 的度数;
(2)∠C 的度数.
A
B
C
D
