直线与双曲线的位置关系(一)[上学期]
图片预览





文档简介
课件17张PPT。直线与双曲线的位置关系
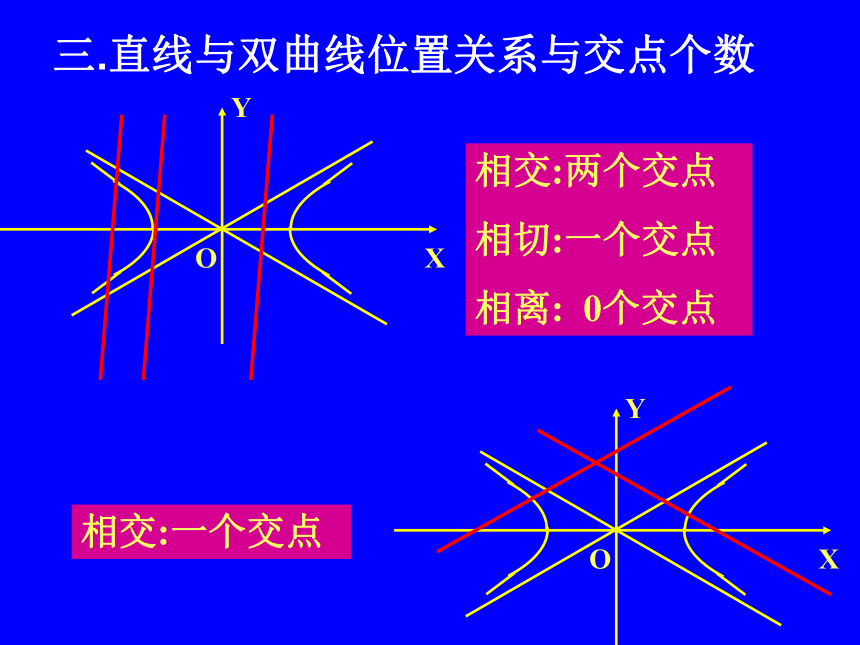
(一)一.复习回顾 二:直线与双曲线位置关系种类种类:相离;相切;相交(两个交点,一个交点)相交:两个交点
相切:一个交点
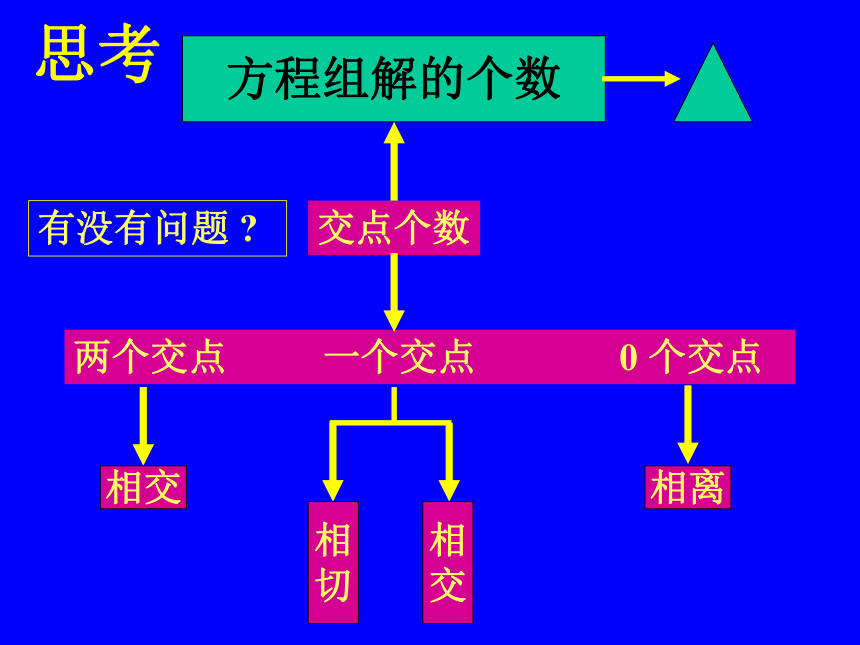
相离: 0个交点相交:一个交点三.直线与双曲线位置关系与交点个数思考两个交点 一个交点 0 个交点相交相
切相
交相离交点个数方程组解的个数有没有问题 ?总结[1] 0 个交点和两个交点的情况都正常,
那么 ,依然可以用判别式判断位置关系[2]一个交点却包括了两种位置关系:
相切和相交 ( 特殊的相交 ) , 那么是否意味着判别式等于零时 , 即可能相切也可能相交 ? 实践是检验真理的唯一标准 !请判断下列直线与双曲线之间的位置关系[1][2]相 切相 交回顾一下:判别式情况如何?一般情况的研究显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何?根本就没有判别式 !判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式判断下列直线与双曲线的位置关系相交(一个交点)相离练习.对任意实数b,直线y=kx+b与x2-2y2=1总有公共点,求k的取值范围。小结:1.判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式作业:<<学习与评价>> 1.2.3.4
(一)一.复习回顾 二:直线与双曲线位置关系种类种类:相离;相切;相交(两个交点,一个交点)相交:两个交点
相切:一个交点
相离: 0个交点相交:一个交点三.直线与双曲线位置关系与交点个数思考两个交点 一个交点 0 个交点相交相
切相
交相离交点个数方程组解的个数有没有问题 ?总结[1] 0 个交点和两个交点的情况都正常,
那么 ,依然可以用判别式判断位置关系[2]一个交点却包括了两种位置关系:
相切和相交 ( 特殊的相交 ) , 那么是否意味着判别式等于零时 , 即可能相切也可能相交 ? 实践是检验真理的唯一标准 !请判断下列直线与双曲线之间的位置关系[1][2]相 切相 交回顾一下:判别式情况如何?一般情况的研究显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何?根本就没有判别式 !判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式判断下列直线与双曲线的位置关系相交(一个交点)相离练习.对任意实数b,直线y=kx+b与x2-2y2=1总有公共点,求k的取值范围。小结:1.判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式作业:<<学习与评价>> 1.2.3.4
