百师联盟2022-2023学年高二上学期开学模拟考数学试题2(Word版含解析)
文档属性
| 名称 | 百师联盟2022-2023学年高二上学期开学模拟考数学试题2(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 02:46:26 | ||
图片预览




文档简介
百师联盟2022-2023学年高二上学期开学模拟考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知为虚数单位,则复数的虚部是( )
A. B. C.2 D.2i
2.在△ABC中,M为边BC上任意一点,N为AM中点,且满足,则的最小值为( )
A. B. C. D.1
3.已知是三个不同的平面,且,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
5.三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用2勾股+(股-勾)=4朱实+黄实=弦实,化简,得勾+股=弦,设勾股中勾股比为,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在红(朱)色图形内的图钉数大约为( )(参考数据:)
A.866 B.500 C.300 D.134
6.已知定点和直线,则点到直线的离的最大值为( )
A. B.
C. D.
7.下列说法正确的是( )
A.从装有个红球和个白球的口袋内任取个球,记事件为“恰有个白球”,事件为恰有个白球”,则与互斥
B.甲 乙二人比赛,甲胜的概率为,则比赛场,甲胜场
C.随机试验的频率与概率相等
D.抛掷一颗质地均匀的骰子,记事件为“向上的点数为或”,事件为“向上的点数为奇数”,则与对立
8.设三棱锥的底面是正三角形,侧棱长均相等,是棱上的点(不含端点),记直线与直线所成角为,直线与平面所成角为,二面角的平面角为,则
A. B.
C. D.
二、多选题
9.已知圆和圆相交于 两点,下列说法正确的为( )
A.两圆有两条公切线 B.直线的方程为
C.线段的长为 D.圆上点,圆上点,的最大值为
10.随机地排列数字1,5,6得到一个三位数,则( )
A.可以排成9个不同的三位数 B.所得的三位数是奇数的概率为
C.所得的三位数是偶数的概率为 D.所得的三位数大于400的概率为
11.正三棱锥底面边长为3,侧棱长为,则下列叙述正确的是( )
A.正三棱锥高为3. B.正三棱锥的斜高为
C.正三棱锥的体积为 D.正三棱锥侧面积为
12.已知函数 则下面叙述正确的是( )
A.最小正周期为 B.在区间是增函数
C.是对称轴 D.最大值为
三、填空题
13.已知直线与,若,则实数a的值为______.
14.某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段
人数(单位:人) 180 180 160 80
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.则抽出的青年观众有______人.
15.费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形最大内角小于时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为.根据以上性质,函数的最小值为__________.
16.在中,分别为三边中点,将分别沿向上折起,使重合,记为,则三棱锥的外接球面积的最小值为________________.
四、解答题
17.已知三个顶点分别为,,.
(1)求经过两边AB和AC的中点的直线的方程;
(2)求的外接圆方程.
18.北京冬季奥运会将于2022年2月4日至2022年2月20日在中华人民共和国北京市和河北省张家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京,张家口同为主办城市,也是中国继北京奥运会,南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解本次培训活动的效果,从中随机抽取80名志愿者的考核成绩,根据这80名志愿者的考核成绩,得到的统计图表如下所示.
女志愿者考核成绩频率分布表
分组 频数 频率
2 0.050
13 0.325
18 0.450
a m
b 0.075
若参加这次考核的志愿者考核成绩在内,则考核等级为优秀
(1)分别求这次培训考核等级为优秀的男、女志愿者人数;
(2)若从样本中考核等级为优秀的志愿者中随机抽取3人进行学习心得分享,记抽到女志愿者的人数为X,求X的分布列及期望.
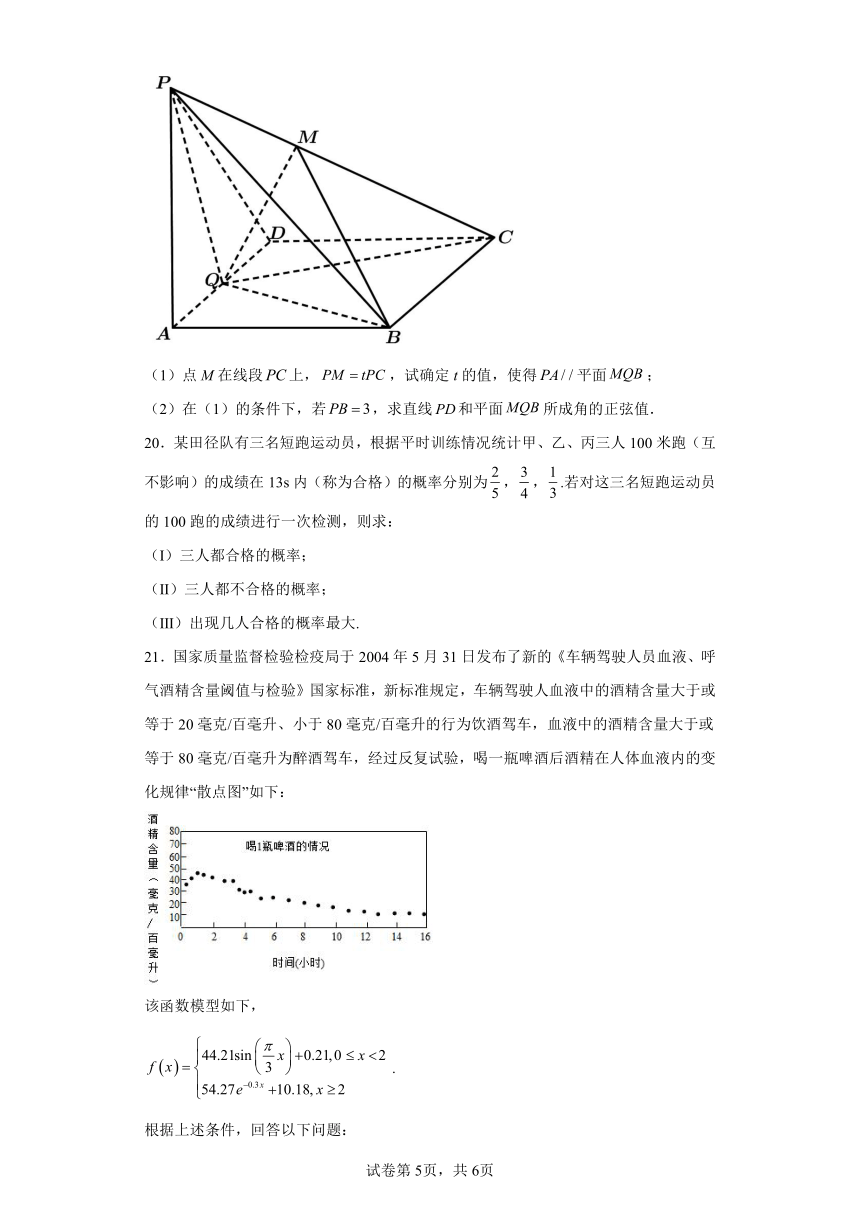
19.如图,在四棱锥中,底面为菱形,,Q为的中点,.
(1)点M在线段上,,试确定t的值,使得平面;
(2)在(1)的条件下,若,求直线和平面所成角的正弦值.
20.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13s内(称为合格)的概率分别为,,.若对这三名短跑运动员的100跑的成绩进行一次检测,则求:
(Ⅰ)三人都合格的概率;
(Ⅱ)三人都不合格的概率;
(Ⅲ)出现几人合格的概率最大.
21.国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,新标准规定,车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下:
该函数模型如下,
.
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据:)
22.如图,在四棱柱中,,,底面ABCD是菱形,,平面平面ABCD,.
(1)证明:平面ABCD;
(2)若M是线段的中点,求二面角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
首先根据复数代数形式的除法运算化简复数,即可判断其虚部;
【详解】
解:
所以复数的虚部为;
故选:C
2.C
【解析】
【分析】
根据给定条件探求出,结合转化为二次函数并求函数的最小值即可.
【详解】
在△ABC中,M为边BC上任意一点,则,
于是得,而,且与不共线,
则,即有,因此,,
当且仅当时取“=”,此时M为BC中点,
所以的最小值为.
故选:C
3.D
【解析】
【分析】
根据几何模型,结合充分条件和必要条件的定义可判断.
【详解】
如图所示,在正方体中,
若为,为,为,则,,满足,但不垂直于,故充分性不成立;
若为,为, 为,则,,满足,但不垂直于,故必要性不成立;
故选:D
4.A
【解析】
【分析】
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
5.A
【解析】
【分析】
计算出朱色的面积、大正方形的面积,然后利用面积比求得图钉数.
【详解】
不妨设勾长,股长,
则朱色面积为,
大正方形的边长为,面积为,
所以落在红(朱)色图形内的图钉数大约为.
故选:A
6.D
【解析】
【分析】
直线,
可化为:,令可得直线经过定点,可得点到直线的距离的最大值为.
【详解】
直线,
可化为:,令解得:
因为直线经过定点,
所以点到直线的距离的最大值为
故选:D
7.A
【解析】
【分析】
直接利用互斥事件和对立事件,频率和概率的关系的应用判断、、、的结论.
【详解】
解:对于:从装有2个红球和2个白球的口袋内任取2个球,记事件为“恰有1个白球”,事件为恰有2个白球”,则与互斥,故正确;
对于:甲、乙二人比赛,甲胜的概率为,并不是说比赛5场,甲胜3场,故错误;
对于:随机试验可以用频率估计概率,并不是说频率和概率相等,故错误;
对于:抛掷一颗质地均匀的骰子,记事件为“向上的点数为1或4”,事件为“向上的点数为奇数”,则与不对立,故错误.
故选:.
8.B
【解析】
本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.
【详解】
方法1:如图为中点,在底面的投影为,则在底面投影在线段上,过作垂直,易得,过作交于,过作,交于,则,则,即,,即,综上所述,答案为B.
方法2:由最小角定理,记的平面角为(显然)
由最大角定理,故选B.
方法3:(特殊位置)取为正四面体,为中点,易得
,故选B.
【点睛】
常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法.
9.ABD
【解析】
【分析】
由给定条件判断圆O与圆M的位置关系,再逐项分析、推理、计算即可作答.
【详解】
圆的圆心,半径,圆的圆心,,
,显然有,于是得圆O与圆M相交,
圆O与圆M有两条公切线,A正确;
由得:,则直线的方程为,B正确;
圆心O到直线:的距离,
则,C不正确;
,当且仅当点E,O,M,F四点共线时取“=”,如图,
因此,当点E,F分别是直线OM与圆O交点,与圆M交点时,,D正确.
故选:ABD
10.BD
【解析】
【分析】
利用列举法列出所有的基本事件,再根据概率公式计算可得结果.
【详解】
随机地排列数字1,5,6可以得到的三位数有:156,165,516,561,615,651,共6个,故A不正确;
其中奇数有:165,561,651,615,共4个,所以所得的三位数是奇数的概率为
,故B正确;
其中偶数有:156,516,共2个,所以所得的三位数是偶数的概率为,故C不正确;
其中大于400的有:516,561,615,651,共4个,所以所得的三位数大于400的概率为,故D正确.
故选:BD
11.AB
【解析】
【分析】
根据题意画出图象,取的中心为,连接,先得出面,再求出,可得正三棱锥高;利用三角形的面积公式求出的面积,利用体积公式求出正三棱锥的体积;作交于,求出正三棱锥的斜高;再利用面积公式求正三棱锥侧面积即可.
【详解】
取的中心为,连接,
由题意得:面,
又为等边三角形,
则,
所以正三棱锥高为:,
,
所以正三棱锥的体积为:,
作交于,
又,
则正三棱锥的斜高为,
所以正三棱锥的侧面积为:.
故选:A B .
【点睛】
本题主要考查了求正三棱锥的高,斜高,侧面积和体积的问题.属于中档题.
12.AC
【解析】
【分析】
利用辅助角公式化简已知可得,结合三角函数的性质依次判断选项即可得解.
【详解】
由题意
对于A,函数的最小正周期,故A正确;
对于B,由,得,令,得,,故B错误;
对于C,由,得,令,得,故C正确;
对于D,,,,即函数的最大值为,故D错误;
故选:AC
【点睛】
方法点睛:函数的性质:
(1) .
(2)周期
(3)由 求对称轴,由求对称中心.
(4)由求增区间;由求减区间.
13.
【解析】
【分析】
由可得,从而可求出实数a的值
【详解】
因为直线与,且,
所以,解得,
故答案为:
14.18
【解析】
【分析】
先计算抽样比,然后根据青年人的人数作乘法可得.
【详解】
由题可知:青年人的人数为360,抽样比为
所以青年人中抽取人数为
故答案为:
【点睛】
本题考查分层抽样的计算,考查概念的理解,属基础题.
15.
【解析】
【分析】
函数表示的是点(x,y)到点C(1,0)的距离与到点B(-1,0),到A(0,2)的距离之和,连接这三个点构成了三角形ABC,由角DOB为,角DOC为,OD=,OC=,OA=,距离之和为:2OC+OA,求和即可.
【详解】
根据题意画出图像并建系,D为坐标原点
函数表示的是点(x,y)到点C(1,0)的距离与到点B(-1,0),到A(0,2)的距离之和,设三角形这个等腰三角形的费马点在高线AD上,设为O点即费马点,连接OB,OC,则角DOB为,角DOC为,B(-1,0)C(1,0),A(0,2),OD=,OC=,OA=,距离之和为:2OC+OA=+=2+.
故答案为.
【点睛】
这个题目考查了点点距的公式,以及解三角形的应用,解三角形的范围问题常见两类,一类是根据基本不等式求范围,注意相等条件的判断;另一类是根据边或角的范围计算,解题时要注意题干信息给出的限制条件.
16.9
【解析】
【分析】
将三棱锥补充成长方体,则对角线长分别为,设长方体的长宽高分别为,推导出,从而,由此能求出三棱锥的外接球面积的最小值.
【详解】
由题意得三棱锥的对棱分别相等,
将三棱锥补充成长方体,
则对角线长分别为,
设长方体的长宽高分别为,
则,
∴,
∵
,
∴,
∴三棱锥的外接球面积的最小值为:
故选D.
【点睛】
本题考查三棱锥外接球的面积的最小值的求法,考查球、圆锥等基础知识,考查运算求解能力、空间想象能力,考查函数与方程思想、数形结合思想,是中档题.
17.(1)
(2)
【解析】
【分析】
(1)求出AB和AC的中点坐标,用两点求直线方程
(2)设圆的一般方程,将三点代入求出参数即可
(1)
AB的中点坐标为,AC的中点坐标为,所以直线的斜率,将代入得直线方程为:,即
(2)
设圆的一般方程为,将三点代入得:
解得: ,所以圆方程为:,化为标准方程为:
18.(1),
(2)分布列见解析,
【解析】
【分析】
(1)由图表数据求解
(2)由超几何分布公式求解
(1)
由女志愿者考核成绩频率分布表可知被抽取的女志愿者的人数为.
因为,所以,
所以这次培训考核等级为优秀的女志愿者人数为.
因为被抽取的志愿者人数是80,所以被抽取的男志愿者人数是.
由男志愿者考核成绩频率分布直方图可知男志愿者这次培训考核等级为优秀的频率为
则这次培训考核等级为优秀的男志愿者人数为.
(2)
由题意可知X的可能取值为.
,
.
X的分布列为
X 0 1 2 3
P
故.
19.(1);(2).
【解析】
【分析】
(1)若平面,易得,再根据,得到求解;
(2)在平面内作于T, 论证平面,然后以点Q为原点,QA为x轴,QB为y轴,建立空间直角坐标系,求得平面的一个法向量,和直线的一个方向向量,设直线和平面所成角为,由求解.
【详解】
(1)当时,平面.
如图所示:
连接交于点N,
连接,由题设,得.
若平面,
由平面平面,得,
所以.
当,
所以,
所以平面.
(2)由题设都是等边三角形,
Q是中点,平面.
,在中,.
因为,
所以.
在平面内作于T,则,.
由平面,可得平面.
以点Q为原点,建立如图所示的空间直角坐标系,
则,
由可得,
所以,
设平面的一个法向量,
则,可取,则,
直线的一个方向向量是,
设直线和平面所成角为,则
所以直线和平面所成角的正弦值等于.
【点睛】
方法点睛:利用向量求线面角的方法:(1)分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.
20.(Ⅰ);(Ⅱ);(Ⅲ)1人.
【解析】
【分析】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,显然事件,,相互独立,则,,,从而根据不同事件的概率求法求得各小题.
【详解】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,
显然事件,,相互独立,则,,
设恰有人合格的概率为.
(Ⅰ)三人都合格的概率:
(Ⅱ)三人都不合格的概率:.
(Ⅲ)恰有两人合格的概率:.
恰有一人合格的概率:.
因为,
所以出现1人合格的概率最大.
21.(1)喝一瓶啤酒后1.5小时血液中的酒精达到最大值,最大值是44.42毫克/百毫升;(2)喝一瓶啤酒后6小时才可以驾车
【解析】
【分析】
(1)由图可知,当函数取得最大值时,,此时时,取得最大值,即可求得.
(2)由题意知当车辆驾驶人员血液中的酒精小于20毫克/100毫升可以驾车,此时,解不等式,两边取对数,即可求出..
【详解】
(1)由图可知,当函数取得最大值时,.
此时.
当时,即时,函数取得最大值为,
故喝一瓶啤酒后1.5小时血液中的酒精达到最大值,最大值是44.42毫克/百毫升,
(2)由题意知当车辆驾驶人员血液中的酒精小于20毫克/100毫升可以驾车,此时,
由,得,
两边取自然对数得,
即,
∴,
故喝一瓶啤酒后6小时才可以驾车.
【点睛】
本题考查函数模型应用和分段函数,考查分析问题的能力和运算求解的能力,属于中档题.
22.(1)证明见解析;
(2).
【解析】
【分析】
(1)连接AC,由线面垂直的判定性质可得,取CD中点E,由面面垂直、线面垂直的性质可得,再利用线面垂直的判定推理作答.
(2)以点C为原点建立空间直角坐标系,借助空间向量求二面角的余弦值作答.
(1)
在四棱柱中,取CD中点E,连接,如图,
菱形中,,因,,平面,则平面,
而平面,即有,因,则是正三角形,,
又平面平面,平面平面,平面,则有平面,
而平面,于是得,又,平面,
所以平面.
(2)
在平面内过点C作,由(1)知,射线两两垂直,
以点C为原点建立如图所示的空间直角坐标系,
则,
,
设平面的一个法向量,则,令,得,
设平面的一个法向量,则,令,得,
于是得,显然二面角的平面角是锐角,
所以二面角的余弦值.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知为虚数单位,则复数的虚部是( )
A. B. C.2 D.2i
2.在△ABC中,M为边BC上任意一点,N为AM中点,且满足,则的最小值为( )
A. B. C. D.1
3.已知是三个不同的平面,且,,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
5.三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用2勾股+(股-勾)=4朱实+黄实=弦实,化简,得勾+股=弦,设勾股中勾股比为,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在红(朱)色图形内的图钉数大约为( )(参考数据:)
A.866 B.500 C.300 D.134
6.已知定点和直线,则点到直线的离的最大值为( )
A. B.
C. D.
7.下列说法正确的是( )
A.从装有个红球和个白球的口袋内任取个球,记事件为“恰有个白球”,事件为恰有个白球”,则与互斥
B.甲 乙二人比赛,甲胜的概率为,则比赛场,甲胜场
C.随机试验的频率与概率相等
D.抛掷一颗质地均匀的骰子,记事件为“向上的点数为或”,事件为“向上的点数为奇数”,则与对立
8.设三棱锥的底面是正三角形,侧棱长均相等,是棱上的点(不含端点),记直线与直线所成角为,直线与平面所成角为,二面角的平面角为,则
A. B.
C. D.
二、多选题
9.已知圆和圆相交于 两点,下列说法正确的为( )
A.两圆有两条公切线 B.直线的方程为
C.线段的长为 D.圆上点,圆上点,的最大值为
10.随机地排列数字1,5,6得到一个三位数,则( )
A.可以排成9个不同的三位数 B.所得的三位数是奇数的概率为
C.所得的三位数是偶数的概率为 D.所得的三位数大于400的概率为
11.正三棱锥底面边长为3,侧棱长为,则下列叙述正确的是( )
A.正三棱锥高为3. B.正三棱锥的斜高为
C.正三棱锥的体积为 D.正三棱锥侧面积为
12.已知函数 则下面叙述正确的是( )
A.最小正周期为 B.在区间是增函数
C.是对称轴 D.最大值为
三、填空题
13.已知直线与,若,则实数a的值为______.
14.某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段
人数(单位:人) 180 180 160 80
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.则抽出的青年观众有______人.
15.费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形最大内角小于时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为.根据以上性质,函数的最小值为__________.
16.在中,分别为三边中点,将分别沿向上折起,使重合,记为,则三棱锥的外接球面积的最小值为________________.
四、解答题
17.已知三个顶点分别为,,.
(1)求经过两边AB和AC的中点的直线的方程;
(2)求的外接圆方程.
18.北京冬季奥运会将于2022年2月4日至2022年2月20日在中华人民共和国北京市和河北省张家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京,张家口同为主办城市,也是中国继北京奥运会,南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解本次培训活动的效果,从中随机抽取80名志愿者的考核成绩,根据这80名志愿者的考核成绩,得到的统计图表如下所示.
女志愿者考核成绩频率分布表
分组 频数 频率
2 0.050
13 0.325
18 0.450
a m
b 0.075
若参加这次考核的志愿者考核成绩在内,则考核等级为优秀
(1)分别求这次培训考核等级为优秀的男、女志愿者人数;
(2)若从样本中考核等级为优秀的志愿者中随机抽取3人进行学习心得分享,记抽到女志愿者的人数为X,求X的分布列及期望.
19.如图,在四棱锥中,底面为菱形,,Q为的中点,.
(1)点M在线段上,,试确定t的值,使得平面;
(2)在(1)的条件下,若,求直线和平面所成角的正弦值.
20.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13s内(称为合格)的概率分别为,,.若对这三名短跑运动员的100跑的成绩进行一次检测,则求:
(Ⅰ)三人都合格的概率;
(Ⅱ)三人都不合格的概率;
(Ⅲ)出现几人合格的概率最大.
21.国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,新标准规定,车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下:
该函数模型如下,
.
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据:)
22.如图,在四棱柱中,,,底面ABCD是菱形,,平面平面ABCD,.
(1)证明:平面ABCD;
(2)若M是线段的中点,求二面角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
首先根据复数代数形式的除法运算化简复数,即可判断其虚部;
【详解】
解:
所以复数的虚部为;
故选:C
2.C
【解析】
【分析】
根据给定条件探求出,结合转化为二次函数并求函数的最小值即可.
【详解】
在△ABC中,M为边BC上任意一点,则,
于是得,而,且与不共线,
则,即有,因此,,
当且仅当时取“=”,此时M为BC中点,
所以的最小值为.
故选:C
3.D
【解析】
【分析】
根据几何模型,结合充分条件和必要条件的定义可判断.
【详解】
如图所示,在正方体中,
若为,为,为,则,,满足,但不垂直于,故充分性不成立;
若为,为, 为,则,,满足,但不垂直于,故必要性不成立;
故选:D
4.A
【解析】
【分析】
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
5.A
【解析】
【分析】
计算出朱色的面积、大正方形的面积,然后利用面积比求得图钉数.
【详解】
不妨设勾长,股长,
则朱色面积为,
大正方形的边长为,面积为,
所以落在红(朱)色图形内的图钉数大约为.
故选:A
6.D
【解析】
【分析】
直线,
可化为:,令可得直线经过定点,可得点到直线的距离的最大值为.
【详解】
直线,
可化为:,令解得:
因为直线经过定点,
所以点到直线的距离的最大值为
故选:D
7.A
【解析】
【分析】
直接利用互斥事件和对立事件,频率和概率的关系的应用判断、、、的结论.
【详解】
解:对于:从装有2个红球和2个白球的口袋内任取2个球,记事件为“恰有1个白球”,事件为恰有2个白球”,则与互斥,故正确;
对于:甲、乙二人比赛,甲胜的概率为,并不是说比赛5场,甲胜3场,故错误;
对于:随机试验可以用频率估计概率,并不是说频率和概率相等,故错误;
对于:抛掷一颗质地均匀的骰子,记事件为“向上的点数为1或4”,事件为“向上的点数为奇数”,则与不对立,故错误.
故选:.
8.B
【解析】
本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.
【详解】
方法1:如图为中点,在底面的投影为,则在底面投影在线段上,过作垂直,易得,过作交于,过作,交于,则,则,即,,即,综上所述,答案为B.
方法2:由最小角定理,记的平面角为(显然)
由最大角定理,故选B.
方法3:(特殊位置)取为正四面体,为中点,易得
,故选B.
【点睛】
常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解法.
9.ABD
【解析】
【分析】
由给定条件判断圆O与圆M的位置关系,再逐项分析、推理、计算即可作答.
【详解】
圆的圆心,半径,圆的圆心,,
,显然有,于是得圆O与圆M相交,
圆O与圆M有两条公切线,A正确;
由得:,则直线的方程为,B正确;
圆心O到直线:的距离,
则,C不正确;
,当且仅当点E,O,M,F四点共线时取“=”,如图,
因此,当点E,F分别是直线OM与圆O交点,与圆M交点时,,D正确.
故选:ABD
10.BD
【解析】
【分析】
利用列举法列出所有的基本事件,再根据概率公式计算可得结果.
【详解】
随机地排列数字1,5,6可以得到的三位数有:156,165,516,561,615,651,共6个,故A不正确;
其中奇数有:165,561,651,615,共4个,所以所得的三位数是奇数的概率为
,故B正确;
其中偶数有:156,516,共2个,所以所得的三位数是偶数的概率为,故C不正确;
其中大于400的有:516,561,615,651,共4个,所以所得的三位数大于400的概率为,故D正确.
故选:BD
11.AB
【解析】
【分析】
根据题意画出图象,取的中心为,连接,先得出面,再求出,可得正三棱锥高;利用三角形的面积公式求出的面积,利用体积公式求出正三棱锥的体积;作交于,求出正三棱锥的斜高;再利用面积公式求正三棱锥侧面积即可.
【详解】
取的中心为,连接,
由题意得:面,
又为等边三角形,
则,
所以正三棱锥高为:,
,
所以正三棱锥的体积为:,
作交于,
又,
则正三棱锥的斜高为,
所以正三棱锥的侧面积为:.
故选:A B .
【点睛】
本题主要考查了求正三棱锥的高,斜高,侧面积和体积的问题.属于中档题.
12.AC
【解析】
【分析】
利用辅助角公式化简已知可得,结合三角函数的性质依次判断选项即可得解.
【详解】
由题意
对于A,函数的最小正周期,故A正确;
对于B,由,得,令,得,,故B错误;
对于C,由,得,令,得,故C正确;
对于D,,,,即函数的最大值为,故D错误;
故选:AC
【点睛】
方法点睛:函数的性质:
(1) .
(2)周期
(3)由 求对称轴,由求对称中心.
(4)由求增区间;由求减区间.
13.
【解析】
【分析】
由可得,从而可求出实数a的值
【详解】
因为直线与,且,
所以,解得,
故答案为:
14.18
【解析】
【分析】
先计算抽样比,然后根据青年人的人数作乘法可得.
【详解】
由题可知:青年人的人数为360,抽样比为
所以青年人中抽取人数为
故答案为:
【点睛】
本题考查分层抽样的计算,考查概念的理解,属基础题.
15.
【解析】
【分析】
函数表示的是点(x,y)到点C(1,0)的距离与到点B(-1,0),到A(0,2)的距离之和,连接这三个点构成了三角形ABC,由角DOB为,角DOC为,OD=,OC=,OA=,距离之和为:2OC+OA,求和即可.
【详解】
根据题意画出图像并建系,D为坐标原点
函数表示的是点(x,y)到点C(1,0)的距离与到点B(-1,0),到A(0,2)的距离之和,设三角形这个等腰三角形的费马点在高线AD上,设为O点即费马点,连接OB,OC,则角DOB为,角DOC为,B(-1,0)C(1,0),A(0,2),OD=,OC=,OA=,距离之和为:2OC+OA=+=2+.
故答案为.
【点睛】
这个题目考查了点点距的公式,以及解三角形的应用,解三角形的范围问题常见两类,一类是根据基本不等式求范围,注意相等条件的判断;另一类是根据边或角的范围计算,解题时要注意题干信息给出的限制条件.
16.9
【解析】
【分析】
将三棱锥补充成长方体,则对角线长分别为,设长方体的长宽高分别为,推导出,从而,由此能求出三棱锥的外接球面积的最小值.
【详解】
由题意得三棱锥的对棱分别相等,
将三棱锥补充成长方体,
则对角线长分别为,
设长方体的长宽高分别为,
则,
∴,
∵
,
∴,
∴三棱锥的外接球面积的最小值为:
故选D.
【点睛】
本题考查三棱锥外接球的面积的最小值的求法,考查球、圆锥等基础知识,考查运算求解能力、空间想象能力,考查函数与方程思想、数形结合思想,是中档题.
17.(1)
(2)
【解析】
【分析】
(1)求出AB和AC的中点坐标,用两点求直线方程
(2)设圆的一般方程,将三点代入求出参数即可
(1)
AB的中点坐标为,AC的中点坐标为,所以直线的斜率,将代入得直线方程为:,即
(2)
设圆的一般方程为,将三点代入得:
解得: ,所以圆方程为:,化为标准方程为:
18.(1),
(2)分布列见解析,
【解析】
【分析】
(1)由图表数据求解
(2)由超几何分布公式求解
(1)
由女志愿者考核成绩频率分布表可知被抽取的女志愿者的人数为.
因为,所以,
所以这次培训考核等级为优秀的女志愿者人数为.
因为被抽取的志愿者人数是80,所以被抽取的男志愿者人数是.
由男志愿者考核成绩频率分布直方图可知男志愿者这次培训考核等级为优秀的频率为
则这次培训考核等级为优秀的男志愿者人数为.
(2)
由题意可知X的可能取值为.
,
.
X的分布列为
X 0 1 2 3
P
故.
19.(1);(2).
【解析】
【分析】
(1)若平面,易得,再根据,得到求解;
(2)在平面内作于T, 论证平面,然后以点Q为原点,QA为x轴,QB为y轴,建立空间直角坐标系,求得平面的一个法向量,和直线的一个方向向量,设直线和平面所成角为,由求解.
【详解】
(1)当时,平面.
如图所示:
连接交于点N,
连接,由题设,得.
若平面,
由平面平面,得,
所以.
当,
所以,
所以平面.
(2)由题设都是等边三角形,
Q是中点,平面.
,在中,.
因为,
所以.
在平面内作于T,则,.
由平面,可得平面.
以点Q为原点,建立如图所示的空间直角坐标系,
则,
由可得,
所以,
设平面的一个法向量,
则,可取,则,
直线的一个方向向量是,
设直线和平面所成角为,则
所以直线和平面所成角的正弦值等于.
【点睛】
方法点睛:利用向量求线面角的方法:(1)分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.
20.(Ⅰ);(Ⅱ);(Ⅲ)1人.
【解析】
【分析】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,显然事件,,相互独立,则,,,从而根据不同事件的概率求法求得各小题.
【详解】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,
显然事件,,相互独立,则,,
设恰有人合格的概率为.
(Ⅰ)三人都合格的概率:
(Ⅱ)三人都不合格的概率:.
(Ⅲ)恰有两人合格的概率:.
恰有一人合格的概率:.
因为,
所以出现1人合格的概率最大.
21.(1)喝一瓶啤酒后1.5小时血液中的酒精达到最大值,最大值是44.42毫克/百毫升;(2)喝一瓶啤酒后6小时才可以驾车
【解析】
【分析】
(1)由图可知,当函数取得最大值时,,此时时,取得最大值,即可求得.
(2)由题意知当车辆驾驶人员血液中的酒精小于20毫克/100毫升可以驾车,此时,解不等式,两边取对数,即可求出..
【详解】
(1)由图可知,当函数取得最大值时,.
此时.
当时,即时,函数取得最大值为,
故喝一瓶啤酒后1.5小时血液中的酒精达到最大值,最大值是44.42毫克/百毫升,
(2)由题意知当车辆驾驶人员血液中的酒精小于20毫克/100毫升可以驾车,此时,
由,得,
两边取自然对数得,
即,
∴,
故喝一瓶啤酒后6小时才可以驾车.
【点睛】
本题考查函数模型应用和分段函数,考查分析问题的能力和运算求解的能力,属于中档题.
22.(1)证明见解析;
(2).
【解析】
【分析】
(1)连接AC,由线面垂直的判定性质可得,取CD中点E,由面面垂直、线面垂直的性质可得,再利用线面垂直的判定推理作答.
(2)以点C为原点建立空间直角坐标系,借助空间向量求二面角的余弦值作答.
(1)
在四棱柱中,取CD中点E,连接,如图,
菱形中,,因,,平面,则平面,
而平面,即有,因,则是正三角形,,
又平面平面,平面平面,平面,则有平面,
而平面,于是得,又,平面,
所以平面.
(2)
在平面内过点C作,由(1)知,射线两两垂直,
以点C为原点建立如图所示的空间直角坐标系,
则,
,
设平面的一个法向量,则,令,得,
设平面的一个法向量,则,令,得,
于是得,显然二面角的平面角是锐角,
所以二面角的余弦值.
答案第1页,共2页
答案第1页,共2页
同课章节目录
