北师大版九年级上册6.1 反比例函数课件(共24张PPT)
文档属性
| 名称 | 北师大版九年级上册6.1 反比例函数课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 803.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第六章 反比例函数
6.1 反比例函数
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据已知条件确定反比例函数的解析式. (重点、难点)
学习目标
我能
一、回顾旧知
1.什么是函数
在某变化过程中有两个变量x,y若给定其中一个变量x的值,y都有唯一确定的值和它对应,则称y是x的函数。
2.一次函数的表达式为 其中k,b为常数且 。
3.正比例函数的表达式为 其中 。
y=kx+b
y=kx
k≠0
k≠0
二、情境引入
?
?
我们知道,导体中的电流I,与导体的电阻R、导体两端的电压U之间满足关系式U=IR,当U=220V时,
R/Ω 20 40 60 80 100 …
I/A
通过填表,你发现 R,I 之间具有怎样的关系?你还能举出这样的例子吗?
11
?
三、讲授新知---反比例函数的概念
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1) 京沪高速铁路全程约为1318 km,某次列车的全程运行时间t (单位:h)随此次列车的平均速度v (单位:km/h)的变化而变化;
(2) 一个矩形的面积为20cm2 ,矩形的长 y (单位:m) 随宽 x (单位:m)的变化而变化;
(3) 某村有耕地346.2hm2 ,人均占有面积 m (hm2/人) 随全村总人口 n (单位:人) 的 变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有 的形式,其中 是常数.
分式
分子
一般地,如果两个变量之间的关系可以表示成 (k为常数,k ≠ 0) 的形式,那么称是反比例函数.
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
①
②
③
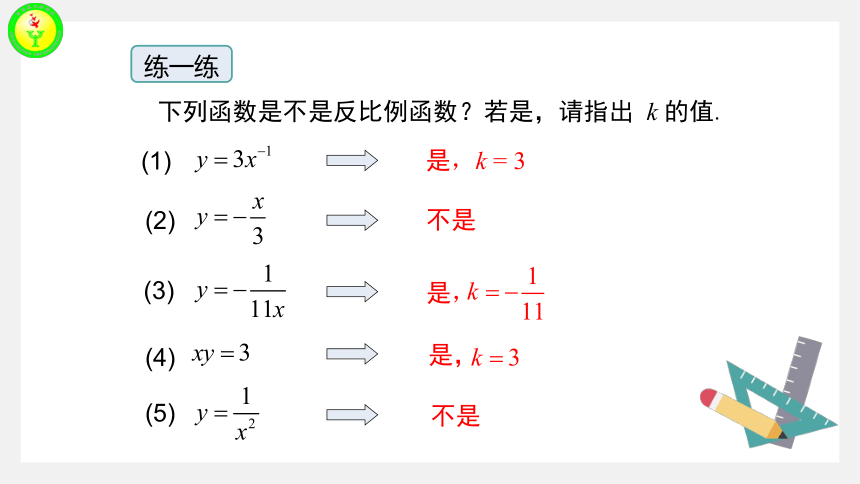
下列函数是不是反比例函数?若是,请指出 k 的值.
是,k = 3
不是
不是
练一练
是,
是,
(1)
(2)
(3)
(4)
(5)
反比例函数:
k≠0 即m-3≠0
解:由题可知m-3≠0,
得m≠3
总结:利用反比例概念求字母值时一定注意k≠0
例1 如果函数 为反比例函数,求m的取值范围
1. 已知函数 是反比例函数,则
k 必须满足 .
2. 当m= 时, 是反比例函数.
k≠-1
±1
练一练
3. 已知函数 是反比例函数,则a=_____
1
讲授新知---确定反比例函数的解析式
例2 已知 y 是 x 的反比例函数,并且当 x=2时,y=6.
写出 y 关于 x 的函数解析式;
提示:因为 y 是 x 的反比例函数,所以设 .把 x=2 和 y=6 代入上式,就可求出常数 k 的值.
解:设 . 因为当 x=2时,y=6,所以有
解得 k =12.
因此
练一练
已知变量 y 与 x 成反比例,且当 x=3时,y=-4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 y=6 时,求 x 的值.
解:(1) 设 . 因为当 x=3时,y=-4,所以有
解得 k =-12.
因此
(2) 把 y=6 代入 ,得
解得 x =-2.
归纳总结
用待定系数法确定反比例函数的表达式的一般步骤
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
你有哪些收获??
四、课堂小结
1.反比例函数的概念:
一般地,如果两个变量之间的关系可以表示成 (k为常数,k ≠ 0) 的形式,那么称是反比例函数.
2.反比例函数三种表达式:
①
②
③
3.用待定系数法确定反比例函数的表达式的一般步骤:
一设,二代,三求,四写.
五、练习巩固
A. B.
C. D.
1. 下列函数中,y是x的反比例函数的是 ( )
A
2. 填空
(1) 若 是反比例函数,则 m 的取值范围
是 .
(2) 若 是反比例函数,则m的取值范
围是 .
(3) 若 是反比例函数,则m的取值范围
是 .
m ≠ 1
m ≠ 0 且 m ≠ -2
m = -1
3. 已知 y 与 x+1 成反比例,并且当 x = 3 时,y = 4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 x = 7 时,求 y 的值.
解:(1) 设 ,因为当 x = 3 时,y =4 ,
所以有 ,解得 k =16,因此 .
(2) 当 x = 7 时,
六、课后思考
4. 已知 y = y1+y2,y1与 (x-1) 成正比例,y2 与 (x + 1)
成反比例,当 x = 0 时,y =-3;当 x =1 时,y = -1,
求:
(1) y 关于 x 的关系式;
解:设 y1 = k1(x-1) (k1≠0), (k2≠0),
则 .
∵ x = 0 时,y =-3;x =1 时,y = -1,
-3=-k1+k2 ,
∴k1=1,k2=-2.
∴
∴
(2) 当 x = 时,y 的值.
解:把 x = 代入 (1) 中函数关系式,得 y =
谢谢聆听
第六章 反比例函数
6.1 反比例函数
1. 理解并掌握反比例函数的概念. (重点)
2. 从实际问题中抽象出反比例函数的概念,能根据已知条件确定反比例函数的解析式. (重点、难点)
学习目标
我能
一、回顾旧知
1.什么是函数
在某变化过程中有两个变量x,y若给定其中一个变量x的值,y都有唯一确定的值和它对应,则称y是x的函数。
2.一次函数的表达式为 其中k,b为常数且 。
3.正比例函数的表达式为 其中 。
y=kx+b
y=kx
k≠0
k≠0
二、情境引入
?
?
我们知道,导体中的电流I,与导体的电阻R、导体两端的电压U之间满足关系式U=IR,当U=220V时,
R/Ω 20 40 60 80 100 …
I/A
通过填表,你发现 R,I 之间具有怎样的关系?你还能举出这样的例子吗?
11
?
三、讲授新知---反比例函数的概念
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1) 京沪高速铁路全程约为1318 km,某次列车的全程运行时间t (单位:h)随此次列车的平均速度v (单位:km/h)的变化而变化;
(2) 一个矩形的面积为20cm2 ,矩形的长 y (单位:m) 随宽 x (单位:m)的变化而变化;
(3) 某村有耕地346.2hm2 ,人均占有面积 m (hm2/人) 随全村总人口 n (单位:人) 的 变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有 的形式,其中 是常数.
分式
分子
一般地,如果两个变量之间的关系可以表示成 (k为常数,k ≠ 0) 的形式,那么称是反比例函数.
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
①
②
③
下列函数是不是反比例函数?若是,请指出 k 的值.
是,k = 3
不是
不是
练一练
是,
是,
(1)
(2)
(3)
(4)
(5)
反比例函数:
k≠0 即m-3≠0
解:由题可知m-3≠0,
得m≠3
总结:利用反比例概念求字母值时一定注意k≠0
例1 如果函数 为反比例函数,求m的取值范围
1. 已知函数 是反比例函数,则
k 必须满足 .
2. 当m= 时, 是反比例函数.
k≠-1
±1
练一练
3. 已知函数 是反比例函数,则a=_____
1
讲授新知---确定反比例函数的解析式
例2 已知 y 是 x 的反比例函数,并且当 x=2时,y=6.
写出 y 关于 x 的函数解析式;
提示:因为 y 是 x 的反比例函数,所以设 .把 x=2 和 y=6 代入上式,就可求出常数 k 的值.
解:设 . 因为当 x=2时,y=6,所以有
解得 k =12.
因此
练一练
已知变量 y 与 x 成反比例,且当 x=3时,y=-4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 y=6 时,求 x 的值.
解:(1) 设 . 因为当 x=3时,y=-4,所以有
解得 k =-12.
因此
(2) 把 y=6 代入 ,得
解得 x =-2.
归纳总结
用待定系数法确定反比例函数的表达式的一般步骤
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
你有哪些收获??
四、课堂小结
1.反比例函数的概念:
一般地,如果两个变量之间的关系可以表示成 (k为常数,k ≠ 0) 的形式,那么称是反比例函数.
2.反比例函数三种表达式:
①
②
③
3.用待定系数法确定反比例函数的表达式的一般步骤:
一设,二代,三求,四写.
五、练习巩固
A. B.
C. D.
1. 下列函数中,y是x的反比例函数的是 ( )
A
2. 填空
(1) 若 是反比例函数,则 m 的取值范围
是 .
(2) 若 是反比例函数,则m的取值范
围是 .
(3) 若 是反比例函数,则m的取值范围
是 .
m ≠ 1
m ≠ 0 且 m ≠ -2
m = -1
3. 已知 y 与 x+1 成反比例,并且当 x = 3 时,y = 4.
(1) 写出 y 关于 x 的函数解析式;
(2) 当 x = 7 时,求 y 的值.
解:(1) 设 ,因为当 x = 3 时,y =4 ,
所以有 ,解得 k =16,因此 .
(2) 当 x = 7 时,
六、课后思考
4. 已知 y = y1+y2,y1与 (x-1) 成正比例,y2 与 (x + 1)
成反比例,当 x = 0 时,y =-3;当 x =1 时,y = -1,
求:
(1) y 关于 x 的关系式;
解:设 y1 = k1(x-1) (k1≠0), (k2≠0),
则 .
∵ x = 0 时,y =-3;x =1 时,y = -1,
-3=-k1+k2 ,
∴k1=1,k2=-2.
∴
∴
(2) 当 x = 时,y 的值.
解:把 x = 代入 (1) 中函数关系式,得 y =
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
