数学人教A版(2019)选择性必修第一册1.4 空间向量的应用 同步课时训练(Word版含解析)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4 空间向量的应用 同步课时训练(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 06:28:54 | ||
图片预览




文档简介
1.4 空间向量的应用--2022-2023学年高二数学人教A版(2019)选择性必修第一册同步课时训练
概念练习
1.如图,某圆锥SO的轴截面SAC是等边三角形,点B是底面圆周上的一点,且,点M是SA的中点,则异面直线AB与CM所成角的余弦值是( )
A. B. C. D.
2.如图,正四棱锥中,O为顶点在底面内的投影,P为侧棱SD的中点,且,则直线BC与平面PAC的夹角是( )
A.30° B.45° C.60° D.90°
3.已知直线过定点,且为其一个方向向量,则点到直线的距离为( )
A. B. C. D.
4.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B.
C. D.
5.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B. C. D.
二、能力提升
6.如图,在长方体中,,,则直线和夹角的余弦值为( )
A. B. C. D.
7.四棱锥中,,,,则这个四棱锥的高h为( )
A.1 B.2 C.3 D.4
(多选)
8.已知二面角的大小为,点,点,,且,,,则两点间的距离可以是( )
A. B. C. 3 D.
9.已知点P是平行四边形ABCD所在的平面外一点,如果,,,则下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
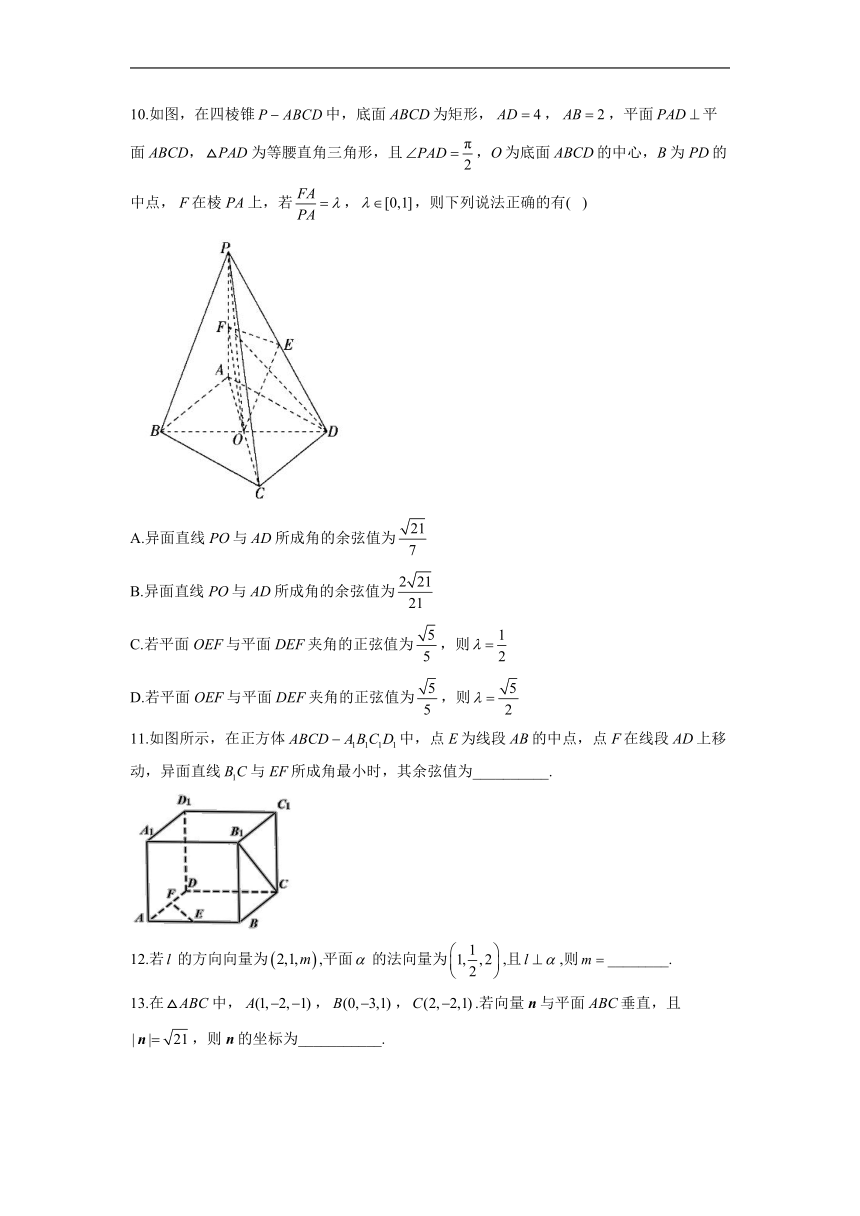
10.如图,在四棱锥中,底面ABCD为矩形,,,平面平面ABCD,为等腰直角三角形,且,O为底面ABCD的中心,B为PD的中点, F在棱PA上,若,,则下列说法正确的有( )
A.异面直线PO与AD所成角的余弦值为
B.异面直线PO与AD所成角的余弦值为
C.若平面OEF与平面DEF夹角的正弦值为,则
D.若平面OEF与平面DEF夹角的正弦值为,则
11.如图所示,在正方体中,点E为线段AB的中点,点F在线段AD上移动,异面直线与EF所成角最小时,其余弦值为__________.
12.若的方向向量为,平面的法向量为,且,则________.
13.在中,,,.若向量n与平面ABC垂直,且,则n的坐标为___________.
14.如图,和都是边长为2的正三角形,且它们所在平面互相垂直.平面,且.
(1)设P是的中点,求证:平面.
(2)求二面角的正弦值.
15.如图,PO是三棱锥的高,,,E是PB的中点.
(1)求证:平面PAC;
(2)若,,,求二面角正余弦值.
答案以及解析
1.答案:C
解析:以过点O且垂直于平面SAC的直线为x轴,直线OC,OS分别为y轴,z轴,
建立如图所示的空间直角坐标系.不妨设,
则根据题意可得,,,,
所以,,
设异面直线AB与CM所成角为,
则.
故选:C.
2.答案:A
解析:如图所示,以为原点建立空间直角坐标系Oxyz.
设,
则.
则,
设平面的法向量为,则,
可求得,
则.
∴,
∴直线与平面所成的角为.
故选A.
3.答案:A
解析:,则点到直线的距离.
4.答案:B
解析:解法一:设H为MF的中点,连接EH,BH,
如图,E是MA的中点,,
是异面直线BE与AF所成的角或其补角,
平面ABC,
,,
,
,
又,,
,
异面直线BE与AF所成角的余弦值为,故选B.
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,
则,
则,
异面直线BE与AF所成角的余弦值为,故选B.
5.答案:B
解析:解法一:设H为MF的中点,连接EH,BH,如图,
E是MA的中点,,是异面直线BE与AF所成的角或其补角.
平面ABC,,
,,
.
F为MC的中点,,
又,
在中,,
,
异面直线BE与AF所成角的余弦值为,故选B.
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,,
则,
异面直线BE与AF所成角的余弦值为,故选B.
6.答案:D
解析:以为原点,分别以,,所在的直线为轴建立空间直角坐标系,则,,,,
所以,,
所以,
所以直线和夹角的余弦值为
7.答案:D
解析:设平面ABCD的法向量为,则,
即,,
取,则,
这个四棱锥的高.故选:D.
8.答案:ABC
解析:如图,设,
,
则
,
,,
结合选项可得,P,Q两点间的距离可以是,,3.
故选:ABC
9.答案:ABC
解析:,,,A对;
,,,B对;
,,,平面ABCD,
是平面ABCD的一个法向量,C对;
,设,即方程组无解,D错.
故选ABC.
10.答案:BC
解析:,
,
平面平面ABCD,
平面平面,平面PAD,
平面ABCD,
底面ABCD为矩形,,AD,AP两两垂直.
以A为原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,如图所示,
则,,,,,
,,
,
异面直线PO与AD所成角的余弦值为,故A错,B对.
由题易得,平面PAD,
取平面PAD的一个法向量.
,,,
,,
设平面OEF的法向量为,
易知,,
则即
令,得,
平面OEF与平面DEF夹角的正弦值为,
,
而,
,解得,
故C对,D错.
故选BC.
11.答案:
解析:以D为坐标原点,建立如图所示的空间直角坐标系,
设正方体的边长为1,则,,,,
所以,,所以,,当异面直线与EF所成角最小时,则最大,即时,.
12.答案:4
解析: ,
的方向向量为 与平面 的法向量为
平行,.
,解得.
故答案为 4 .
13.答案:或
解析:据题意,得,.设,n与平面ABC垂直,即可得,,解得或.当时,,;当时,,.
14.答案:(1)见解析
(2)
解析:(1)证明:取的中点O,连接.
是正三角形,
.
∵平面平面,平面平面,
平面.
平面,
.
在中,,
.
又,
为等腰三角形.
是的中点,.
平面,
.
平面平面,
平面.
(2)由(1)知,,
∴四边形为平行四边形,
,
.
以点O为坐标原点,以的方向分别为x轴、y轴、z轴的正方向,建立如图的空间直角坐标系,
则, ,
.
设平面的法向量为,
则即
令,则,
.
设平面的法向量为,
则即
令,则,
.
.
,
∴二面角的正弦值为.
15.答案:(1)证明见解析
(2)
解析:(1)如图,取AB的中点D,连接DP,DO,DE.
因为,所以.
因为PO为三棱锥的高,所以平面ABC,
因为平面ABC,所以.
又平面POD,且,所以平面POD.
因为平面POD,所以,
又,所以,因为平面PAC,平面PAC,所以平面PAC.
因为D,E分别为BA,BP的中点,所以,
因为平面PAC,平面PAC,所以平面PAC.
又平面ODE,,
所以平面平面PAC.
又平面ODE,所以平面PAC.
(2)连接OA,
因为平面ABC,平面ABC,
所以,,
所以.
易得在中,,
所以,,
又,
所以在中,.
以A为坐标原点,AB,AC所在直线分别为x,y轴,以过A且垂直于平面ABC的直线为z轴建立空间直角坐标系,如图所示,则,,,,,
设平面AEC的法向量为,
则,即,
令,则.
设平面AEB的法向量为,
则,即,令,则.
所以.
设二面角的大小为,
则.
概念练习
1.如图,某圆锥SO的轴截面SAC是等边三角形,点B是底面圆周上的一点,且,点M是SA的中点,则异面直线AB与CM所成角的余弦值是( )
A. B. C. D.
2.如图,正四棱锥中,O为顶点在底面内的投影,P为侧棱SD的中点,且,则直线BC与平面PAC的夹角是( )
A.30° B.45° C.60° D.90°
3.已知直线过定点,且为其一个方向向量,则点到直线的距离为( )
A. B. C. D.
4.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B.
C. D.
5.如图,在三棱锥中,平面ABC,是边长为2的正三角形,,E,F分别为MA,MC的中点,则异面直线BE与AF所成角的余弦值为( )
A. B. C. D.
二、能力提升
6.如图,在长方体中,,,则直线和夹角的余弦值为( )
A. B. C. D.
7.四棱锥中,,,,则这个四棱锥的高h为( )
A.1 B.2 C.3 D.4
(多选)
8.已知二面角的大小为,点,点,,且,,,则两点间的距离可以是( )
A. B. C. 3 D.
9.已知点P是平行四边形ABCD所在的平面外一点,如果,,,则下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
10.如图,在四棱锥中,底面ABCD为矩形,,,平面平面ABCD,为等腰直角三角形,且,O为底面ABCD的中心,B为PD的中点, F在棱PA上,若,,则下列说法正确的有( )
A.异面直线PO与AD所成角的余弦值为
B.异面直线PO与AD所成角的余弦值为
C.若平面OEF与平面DEF夹角的正弦值为,则
D.若平面OEF与平面DEF夹角的正弦值为,则
11.如图所示,在正方体中,点E为线段AB的中点,点F在线段AD上移动,异面直线与EF所成角最小时,其余弦值为__________.
12.若的方向向量为,平面的法向量为,且,则________.
13.在中,,,.若向量n与平面ABC垂直,且,则n的坐标为___________.
14.如图,和都是边长为2的正三角形,且它们所在平面互相垂直.平面,且.
(1)设P是的中点,求证:平面.
(2)求二面角的正弦值.
15.如图,PO是三棱锥的高,,,E是PB的中点.
(1)求证:平面PAC;
(2)若,,,求二面角正余弦值.
答案以及解析
1.答案:C
解析:以过点O且垂直于平面SAC的直线为x轴,直线OC,OS分别为y轴,z轴,
建立如图所示的空间直角坐标系.不妨设,
则根据题意可得,,,,
所以,,
设异面直线AB与CM所成角为,
则.
故选:C.
2.答案:A
解析:如图所示,以为原点建立空间直角坐标系Oxyz.
设,
则.
则,
设平面的法向量为,则,
可求得,
则.
∴,
∴直线与平面所成的角为.
故选A.
3.答案:A
解析:,则点到直线的距离.
4.答案:B
解析:解法一:设H为MF的中点,连接EH,BH,
如图,E是MA的中点,,
是异面直线BE与AF所成的角或其补角,
平面ABC,
,,
,
,
又,,
,
异面直线BE与AF所成角的余弦值为,故选B.
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,
则,
则,
异面直线BE与AF所成角的余弦值为,故选B.
5.答案:B
解析:解法一:设H为MF的中点,连接EH,BH,如图,
E是MA的中点,,是异面直线BE与AF所成的角或其补角.
平面ABC,,
,,
.
F为MC的中点,,
又,
在中,,
,
异面直线BE与AF所成角的余弦值为,故选B.
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,,
则,
异面直线BE与AF所成角的余弦值为,故选B.
6.答案:D
解析:以为原点,分别以,,所在的直线为轴建立空间直角坐标系,则,,,,
所以,,
所以,
所以直线和夹角的余弦值为
7.答案:D
解析:设平面ABCD的法向量为,则,
即,,
取,则,
这个四棱锥的高.故选:D.
8.答案:ABC
解析:如图,设,
,
则
,
,,
结合选项可得,P,Q两点间的距离可以是,,3.
故选:ABC
9.答案:ABC
解析:,,,A对;
,,,B对;
,,,平面ABCD,
是平面ABCD的一个法向量,C对;
,设,即方程组无解,D错.
故选ABC.
10.答案:BC
解析:,
,
平面平面ABCD,
平面平面,平面PAD,
平面ABCD,
底面ABCD为矩形,,AD,AP两两垂直.
以A为原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,如图所示,
则,,,,,
,,
,
异面直线PO与AD所成角的余弦值为,故A错,B对.
由题易得,平面PAD,
取平面PAD的一个法向量.
,,,
,,
设平面OEF的法向量为,
易知,,
则即
令,得,
平面OEF与平面DEF夹角的正弦值为,
,
而,
,解得,
故C对,D错.
故选BC.
11.答案:
解析:以D为坐标原点,建立如图所示的空间直角坐标系,
设正方体的边长为1,则,,,,
所以,,所以,,当异面直线与EF所成角最小时,则最大,即时,.
12.答案:4
解析: ,
的方向向量为 与平面 的法向量为
平行,.
,解得.
故答案为 4 .
13.答案:或
解析:据题意,得,.设,n与平面ABC垂直,即可得,,解得或.当时,,;当时,,.
14.答案:(1)见解析
(2)
解析:(1)证明:取的中点O,连接.
是正三角形,
.
∵平面平面,平面平面,
平面.
平面,
.
在中,,
.
又,
为等腰三角形.
是的中点,.
平面,
.
平面平面,
平面.
(2)由(1)知,,
∴四边形为平行四边形,
,
.
以点O为坐标原点,以的方向分别为x轴、y轴、z轴的正方向,建立如图的空间直角坐标系,
则, ,
.
设平面的法向量为,
则即
令,则,
.
设平面的法向量为,
则即
令,则,
.
.
,
∴二面角的正弦值为.
15.答案:(1)证明见解析
(2)
解析:(1)如图,取AB的中点D,连接DP,DO,DE.
因为,所以.
因为PO为三棱锥的高,所以平面ABC,
因为平面ABC,所以.
又平面POD,且,所以平面POD.
因为平面POD,所以,
又,所以,因为平面PAC,平面PAC,所以平面PAC.
因为D,E分别为BA,BP的中点,所以,
因为平面PAC,平面PAC,所以平面PAC.
又平面ODE,,
所以平面平面PAC.
又平面ODE,所以平面PAC.
(2)连接OA,
因为平面ABC,平面ABC,
所以,,
所以.
易得在中,,
所以,,
又,
所以在中,.
以A为坐标原点,AB,AC所在直线分别为x,y轴,以过A且垂直于平面ABC的直线为z轴建立空间直角坐标系,如图所示,则,,,,,
设平面AEC的法向量为,
则,即,
令,则.
设平面AEB的法向量为,
则,即,令,则.
所以.
设二面角的大小为,
则.
