九年级上册22.3 实际问题与二次函数课件(共20张PPT)
文档属性
| 名称 | 九年级上册22.3 实际问题与二次函数课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 478.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 20:36:14 | ||
图片预览







文档简介
(共20张PPT)
第二十二章 二次函数
22.3 实际问题与二次函数
(第1课时)
人教版 九年级上册
学习目标
1.能够表示实际问题中变量之间的二次函数关系
2.会运用二次函数的顶点坐标求出实际问题的最值.
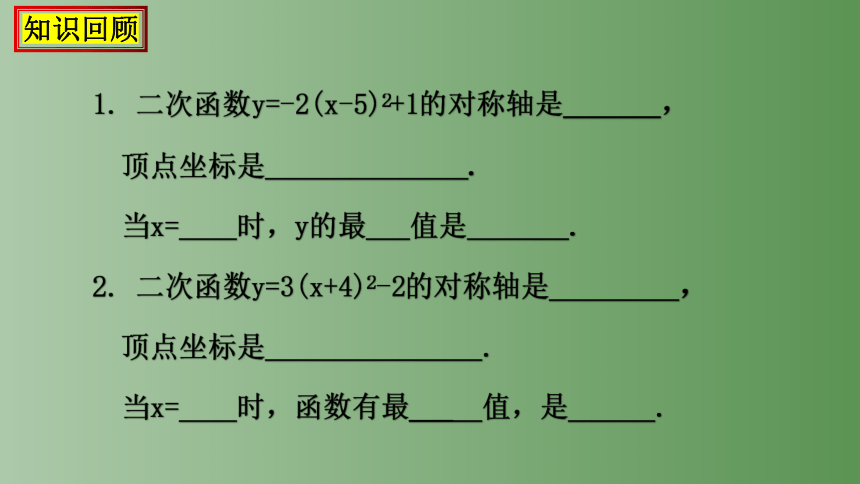
1. 二次函数y=-2(x-5)2+1的对称轴是 ,
顶点坐标是 .
当x= 时,y的最 值是 .
2. 二次函数y=3(x+4)2-2的对称轴是 ,
顶点坐标是 .
当x= 时,函数有最___ 值,是 .
知识回顾
3.二次函数y=2x2-4x+1的对称轴是 ,
顶点坐标是 .
当x= 时,函数有最__ 值,是 .
知识回顾
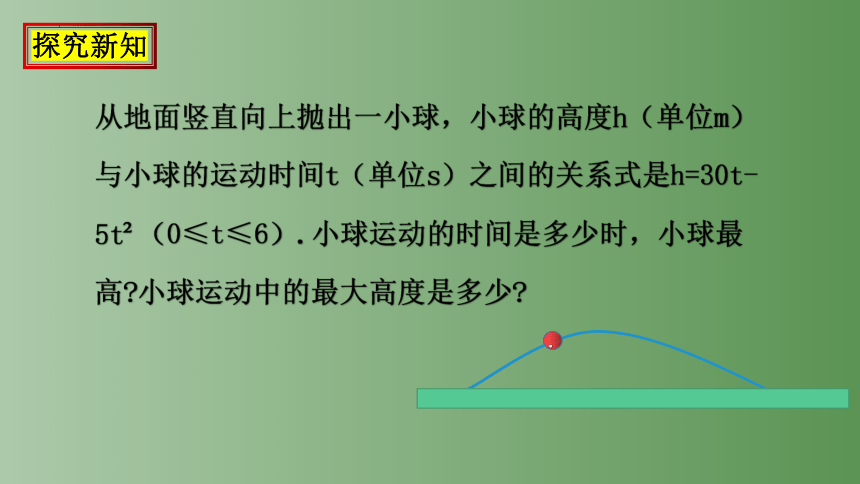
从地面竖直向上抛出一小球,小球的高度h(单位m)与小球的运动时间t(单位s)之间的关系式是h=30t-5t (0≤t≤6).小球运动的时间是多少时,小球最高 小球运动中的最大高度是多少
探究新知
.
从地面竖直向上抛出一小球,小球的高度h(单位m)与小球的运动时间t(单位s)之间的关系式是h=30t-5t (0≤t≤6).小球运动的时间是多少时,小球最高 小球运动中的最大高度是多少
探究新知
即:小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
由于抛物线 y = ax 2 + bx + c 的顶点
是最低(高)点,
问题拓展
如何求出二次函数
y = ax 2 + bx + c 的最小(大)值
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长x的变化而变化.当x是多少时,场地的面积S最大?
解:矩形场地的周长是60m,一边长为xm,
另一边长为(30-x)m
场地的面积
S=x(30-x)
=-x2+30x= -(x-15)2+225
跟踪练习
当x是15m时,场地的面积S最大.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙,另三边用总长为 40 m 的栅栏围住(如下图).设绿化带的AB边长为 x m,绿化带的面积为 y m 2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
拓展训练
解:(1)AB=xm,BC=40-2x
y=x(40-2x)=-2x2 +40x (7.5≤x≤25)
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙,另三边用总长为 40 m 的栅栏围住(如下图).设绿化带的AB边长为 x m,绿化带的面积为 y m 2.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
拓展训练
(2)y=-2x2 +40x
(2)y=-2(x-10)2 +200
x=10时,满足条件的绿化带的面积最大
(2)当y=16时,-x2+10x=16.
解得x1=2,x2=8.
∴10-x=8或2.
答:矩形的长和宽分别为8 cm和2 cm.
用20cm长的铁丝围矩形设矩形一边长为x cm,面积为ycm2.
(1)求y与x的函数关系式
(2)当所围矩形的面积是16cm2,时,求所围矩形的长和宽;
跟踪练习
(1)y=(10-x)x=-x2+10x
用20cm长的铁丝围矩形设矩形一边长为x cm,面积为ycm2.
(3)当x为多少时所围矩形面积最大;最大面积是多少?
跟踪练习
(3)y=-x2+10x
=-(x-5)2+25
当x为5cm时,所围矩形面积最大;最大面积是25cm2
某商店经营T恤衫,已知成批购进时单价是20元.根据市场调查,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
解:设销售单价为x元,利润为y元
则一件的利润为 .
(x-20)元
销售量为 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
10(100-x)+200=-10x+1200
化简为 .
利润为 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
y=(x-20)(-10x-1200)
y=-10x2-1000x+24000
答:销售单价是50元时,获利最多,最大利润是49000元.
配方得 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多 最大利润是多少?
探究新知
y=-10(x-50)2+49000
总结归纳
一般情况,营销利润最值问题建模思想:
(1)审题
(2)用自变量表示一件的利润
(3)用自变量表示销售量
(4)列解析式:总利润=一件的利润×销售量
(5)求出函数的最值
(6)答
1.如图在长200米,宽80米的矩形广场内修建等宽的十字形道路.绿地面积y(㎡)与x路宽(m)之间的关系?
堂检测纳
解:y=(200-x)(80-x)
y=x2 -280x+16000
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;已知商品的进价为每件40元,如何定价才能使利润最大?
堂检测纳
解:设销售单价为x元,利润为y元
y=(60-40+x)[300-10(x-60))]
化简得:y=-10x2+700x+18000
y=-10(x-35)2+30250
答:定价35元才能使利润最大
坚持就是胜利
第二十二章 二次函数
22.3 实际问题与二次函数
(第1课时)
人教版 九年级上册
学习目标
1.能够表示实际问题中变量之间的二次函数关系
2.会运用二次函数的顶点坐标求出实际问题的最值.
1. 二次函数y=-2(x-5)2+1的对称轴是 ,
顶点坐标是 .
当x= 时,y的最 值是 .
2. 二次函数y=3(x+4)2-2的对称轴是 ,
顶点坐标是 .
当x= 时,函数有最___ 值,是 .
知识回顾
3.二次函数y=2x2-4x+1的对称轴是 ,
顶点坐标是 .
当x= 时,函数有最__ 值,是 .
知识回顾
从地面竖直向上抛出一小球,小球的高度h(单位m)与小球的运动时间t(单位s)之间的关系式是h=30t-5t (0≤t≤6).小球运动的时间是多少时,小球最高 小球运动中的最大高度是多少
探究新知
.
从地面竖直向上抛出一小球,小球的高度h(单位m)与小球的运动时间t(单位s)之间的关系式是h=30t-5t (0≤t≤6).小球运动的时间是多少时,小球最高 小球运动中的最大高度是多少
探究新知
即:小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
由于抛物线 y = ax 2 + bx + c 的顶点
是最低(高)点,
问题拓展
如何求出二次函数
y = ax 2 + bx + c 的最小(大)值
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长x的变化而变化.当x是多少时,场地的面积S最大?
解:矩形场地的周长是60m,一边长为xm,
另一边长为(30-x)m
场地的面积
S=x(30-x)
=-x2+30x= -(x-15)2+225
跟踪练习
当x是15m时,场地的面积S最大.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙,另三边用总长为 40 m 的栅栏围住(如下图).设绿化带的AB边长为 x m,绿化带的面积为 y m 2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
拓展训练
解:(1)AB=xm,BC=40-2x
y=x(40-2x)=-2x2 +40x (7.5≤x≤25)
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙,另三边用总长为 40 m 的栅栏围住(如下图).设绿化带的AB边长为 x m,绿化带的面积为 y m 2.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
拓展训练
(2)y=-2x2 +40x
(2)y=-2(x-10)2 +200
x=10时,满足条件的绿化带的面积最大
(2)当y=16时,-x2+10x=16.
解得x1=2,x2=8.
∴10-x=8或2.
答:矩形的长和宽分别为8 cm和2 cm.
用20cm长的铁丝围矩形设矩形一边长为x cm,面积为ycm2.
(1)求y与x的函数关系式
(2)当所围矩形的面积是16cm2,时,求所围矩形的长和宽;
跟踪练习
(1)y=(10-x)x=-x2+10x
用20cm长的铁丝围矩形设矩形一边长为x cm,面积为ycm2.
(3)当x为多少时所围矩形面积最大;最大面积是多少?
跟踪练习
(3)y=-x2+10x
=-(x-5)2+25
当x为5cm时,所围矩形面积最大;最大面积是25cm2
某商店经营T恤衫,已知成批购进时单价是20元.根据市场调查,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
解:设销售单价为x元,利润为y元
则一件的利润为 .
(x-20)元
销售量为 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
10(100-x)+200=-10x+1200
化简为 .
利润为 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多
探究新知
y=(x-20)(-10x-1200)
y=-10x2-1000x+24000
答:销售单价是50元时,获利最多,最大利润是49000元.
配方得 .
某网店经营T恤衫,已知成批购进时单价是20元.网店店主发现,销售量与销售单价满足如下关系:在某一时间内,单价是100元时,销售量是200件,而单价每降低1元,就可以多售出10件. 销售单价是多少时,可以获利最多 最大利润是多少?
探究新知
y=-10(x-50)2+49000
总结归纳
一般情况,营销利润最值问题建模思想:
(1)审题
(2)用自变量表示一件的利润
(3)用自变量表示销售量
(4)列解析式:总利润=一件的利润×销售量
(5)求出函数的最值
(6)答
1.如图在长200米,宽80米的矩形广场内修建等宽的十字形道路.绿地面积y(㎡)与x路宽(m)之间的关系?
堂检测纳
解:y=(200-x)(80-x)
y=x2 -280x+16000
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;已知商品的进价为每件40元,如何定价才能使利润最大?
堂检测纳
解:设销售单价为x元,利润为y元
y=(60-40+x)[300-10(x-60))]
化简得:y=-10x2+700x+18000
y=-10(x-35)2+30250
答:定价35元才能使利润最大
坚持就是胜利
同课章节目录
