金牌培训2022-2023学年高一上开学考试数学试题1(Word版含解析)
文档属性
| 名称 | 金牌培训2022-2023学年高一上开学考试数学试题1(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 09:57:35 | ||
图片预览



文档简介
金牌培训2022-2023学年高一上开学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.把多项式分解因式,结果是( )
A. B.
C. D.
2.如图,、、是同一平面内的三条平行直线,与间的距离是1,与间的距离是2,正三角形的三顶点分别在、、上,则的边长是( )
A. B. C. D.
3.如图,将一个含有45°角的直角三角板摆放在矩形上,若∠1=25°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
4.南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积术”,其求法是:“以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,为实;一为从隅,开平方得积.”若把以上这段文字写成公式,即,其中、、是内角、、的对边.若,,则的面积为( )
A. B. C. D.
5.若集合中有且仅有一个元素,则实数的值为( )
A. B. C. D.
6.设集合,且,则( )
A. B. C.1 D.2
7.在△中,是上的点,平分,,则( )
A. B. C. D.
8.已知命题,,则命题的否定为
A., B.,
C., D.,
二、多选题
9.下列函数中,最小值为2的是
A.
B.
C.
D.
10.下列说法中正确的是( )
A.两条对角线互相垂直且平分的四边形是菱形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直、平分且相等的四边形是正方形
D.两条对角线互相平分的四边形是平行四边形
11.下列结论错误的有
A.两个不等式与成立的条件是相同的
B.已知,则的最大值为5
C.函数的最小值等于4
D.且是的充要条件
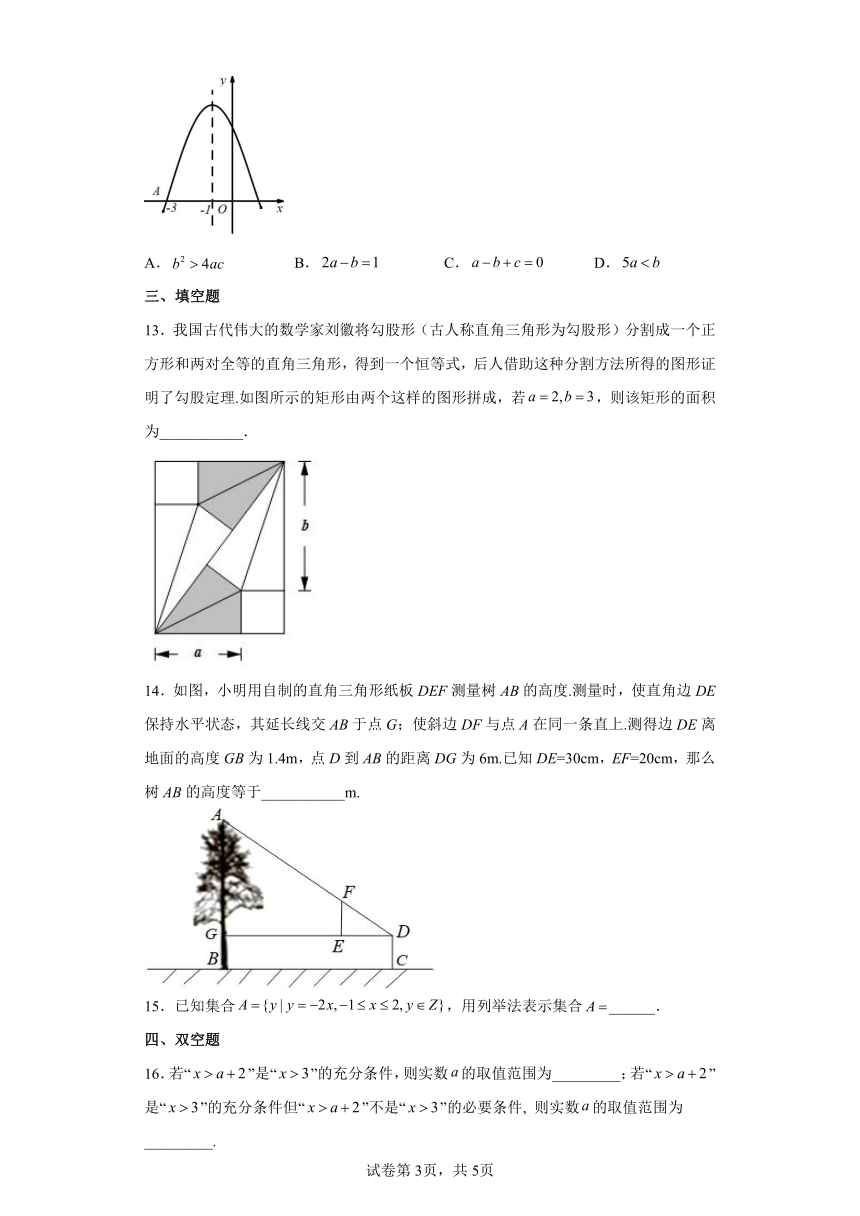
12.如图是二次函数图象的一部分,图象过点,且对称轴为,则以下选项中正确的为( )
A. B. C. D.
三、填空题
13.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若,则该矩形的面积为___________.
14.如图,小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m.已知DE=30cm,EF=20cm,那么树AB的高度等于___________m.
15.已知集合,用列举法表示集合______.
四、双空题
16.若“”是“”的充分条件,则实数的取值范围为_________;若“”是“”的充分条件但“”不是“”的必要条件, 则实数的取值范围为_________.
五、解答题
17.(1)先化简再求值:,其中a=,b=.
(2)
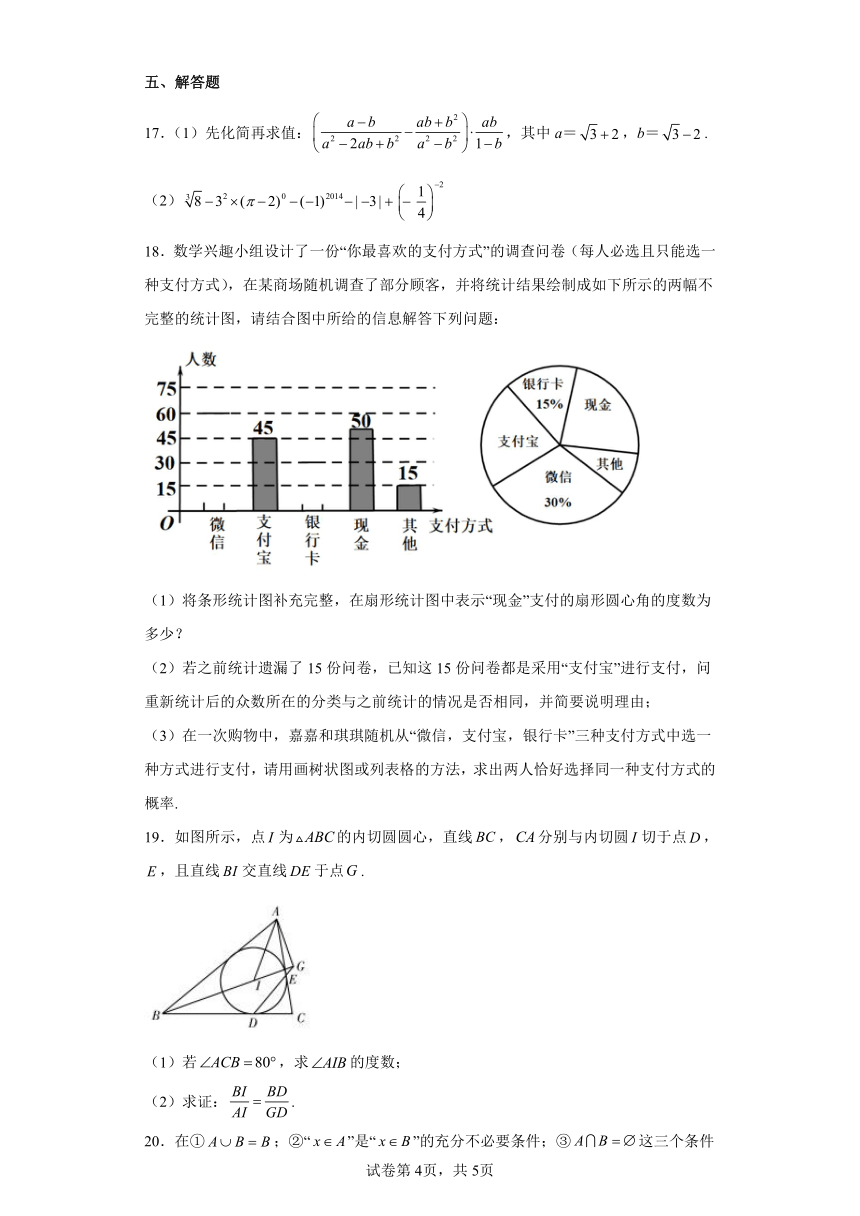
18.数学兴趣小组设计了一份“你最喜欢的支付方式”的调查问卷(每人必选且只能选一种支付方式),在某商场随机调查了部分顾客,并将统计结果绘制成如下所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)将条形统计图补充完整,在扇形统计图中表示“现金”支付的扇形圆心角的度数为多少?
(2)若之前统计遗漏了15份问卷,已知这15份问卷都是采用“支付宝”进行支付,问重新统计后的众数所在的分类与之前统计的情况是否相同,并简要说明理由;
(3)在一次购物中,嘉嘉和琪琪随机从“微信,支付宝,银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
19.如图所示,点为的内切圆圆心,直线,分别与内切圆切于点,,且直线交直线于点.
(1)若,求的度数;
(2)求证:.
20.在①;②“”是“”的充分不必要条件;③这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
问题:已知集合,.
(1)当时,求;
(2)若______,求实数a的取值范围.
21.解方程
(1)x2+2x-3=0;
(2).
22.若二次函数满足且.
(1)求的解析式;
(2)是否存在实数,使函数的最小值为2?若存在,求出的值;若不存在,说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
先利用分组分解法得,再利用平方差公式分解因式即可
【详解】
解:,
故选:B
2.D
【解析】
【详解】
作高AE,BG,CF(如图),
设AD=x,则AC=3x,
于是,,
∵∠BDG=∠CDF,
∠BGD=∠CFD=90°,
∴Rt△BDG∽Rt△CDF,
,即,
.
故选:D.
3.A
【解析】
【分析】
直角利用三角形外角的性质,结合平行四边形的性质,即可求解.
【详解】
由题意,因为,,所以,
又因为矩形对边平行,所以,
故选:A
4.A
【解析】
【分析】
利用余弦定理以及题中等式可求得的面积.
【详解】
由余弦定理可得,所以,,
所以,.
故选:A.
5.C
【解析】
【分析】
讨论与方程有一实根即可求解.
【详解】
当时,,符合题意;
当时,有一实根,所以,符合题意;
所以实数的值为或
故选:C
6.D
【解析】
【分析】
求得集合和,根据题意,得到,即可求解.
【详解】
解:由题意,集合,,
因为,可得,解得.
故选:D.
7.C
【解析】
【分析】
过点作,延长与交于点,可证明△∽△,结合平分,可得,,从而可知.
【详解】
过点作,延长与交于点,
则,所以△∽△,且,
又因为平分,所以,
故△是等腰三角形,且,
所以.
故选:C.
【点睛】
本题考查角分线、相似三角形的性质,考查学生的推理能力,属于基础题.
8.A
【解析】
【分析】
根据全程命题的否定是特称命题,这一规则书写即可.
【详解】
全称命题“,”的否定为特称命题,故命题的否定为“,”.
故答案为A.
【点睛】
这个题目考查了全称命题的否定的写法,换量词否结论,不变条件.
9.AB
【解析】
对A,根据二次函数的最值判定即可.
对B,利用基本不等式判定即可.
对C,利用基本不等式判定即可.
对D,根据指数函数的值域判定即可.
【详解】
对A, ,当且仅当时取等号.故A正确.
对B, ,当且仅当时取等号.故B正确.
对C, .取等号时,又故不可能成立.故C错误 .
对D,因为,故.故D错误.
故选:AB
【点睛】
本题主要考查了函数最值的运算,属于基础题.
10.ACD
【解析】
【分析】
利用菱形的判定,矩形的判定,正方形的判定依次判断可求解.
【详解】
对于选项A,两条对角线互相垂直且平分的四边形是菱形,故A说法正确;
对于选项B,两条对角线相等的平行四边形是矩形,故B说法错误;
对于选项C,两条对角线互相垂直、平分且相等的四边形是正方形,故C说法正确;
对于选项D,两条对角线互相平分的四边形是平行四边形,故D说法正确;
故选:ACD.
11.ABCD
【解析】
根据基本不等式等号成立的条件,重要不等式、基本不等式的应用条件逐项分析即可.
【详解】
A中成立条件为,成立条件为,故不正确;
B中, 因为,所以,最大值不是5,错误;
C中,,故,当且仅当时,等号成立,故等号取不到,错误;
D中,当且时,,当且仅当时等号成立,取时,不能得到且,故且是的充分不必要条件,故错误.
故选:ABCD
【点睛】
本题主要考查了重要不等式、基本不等式的成立条件,应用基本不等式求最值的等号成立条件,属于中档题.
12.AD
【解析】
【分析】
由抛物线的开口方向,对称轴,及特殊点代入可判断选项.
【详解】
A:∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴,即,故A正确;
B:∵对称轴为,
∴,即,故B错误;
C:由图象可知当时,,即,故C错误;
D:∵把代入解析式可得,
两式相加整理可得,
又当时,,
则,故D正确.
故选:AD.
【点睛】
二次函数的相关量判断:开口方向、对称轴、根的判别式、零点是常用的切入点.
13.12
【解析】
设小正方形的边长为,在中由勾股定理得,则可求出面积.
【详解】
设小正方形的边长为,
,,
在中,,
即,即,
则该矩形的面积为.
故答案为:12.
14.5.4
【解析】
【分析】
由题意,由此得线段之间的比例关系,建立方程组,解之可得答案.
【详解】
解:根据题意得,所以,又,所以,解得,
又,所以m,
故答案为:5.4.
15.0,1,
【解析】
【分析】
先由x的范围推出y的范围,然后从中取整数即可.
【详解】
因为,,即,
又,,,,,,,
故答案为0,1,
【点睛】
本题考查了集合的表示法属基础题.
16.
【解析】
【分析】
根据充分条件以及必要条件的定义集合的包含关系得出实数的取值范围.
【详解】
∵若“”是“”的充分条件,∴,∴
∵若“”是“”的充分条件但“”不是“”的必要条件,
∴,∴
故答案为:,
【点睛】
关键点睛:解决本题的关键在于将充分条件以及必要条件的问题转化为集合的包含关系,由集合的知识进行求解.
17.(1);(2)5.
【解析】
【分析】
(1)先根据分式混合运算的法则把原式进行化简,再把的值代入进行计算即可;
(2)指数幂的运算法则和绝对值的含义,即可求出结果.
【详解】
(1)原式=
;
当时,
,
,
∴原式.
(2).
18.(1)条形统计图见解析,;(2)不同,理由见解析;(3).
【解析】
【分析】
(1)由两幅图可知,用现金、支付宝、其他支付共有人数110人,所占比例为1-15%-30%=55%,可得共调查了多少人,再根据用银行卡、微信支付的百分比可得答案
(2)根据原数据的众数所在的分类为微信,加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝可得答案;
(3)将微信记为A、支付宝记为B、银行卡记为C,画出树状图根据古典概型概率计算公式可得答案.
【详解】
(1)由条形统计图可知,用现金、支付宝、其他支付共有人数110人,
所占比例为1-15%-30%=55%,所以共调查了人,
所以用银行卡支付的人有人,用微信支付的人有人,
用现金支付所占比例为,所以,在扇形统计图中表示“现金”支付的扇形圆心角的度数为90°,
补全统计图如图所示:
(2)重新统计后的众数所在的分类与之前统计的情况不同,理由如下:原数据的众数所在的分类为微信,而加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝.
(3)将微信记为A、支付宝记为B、银行卡记为C,画树状图如下:
∵共有9种等可能的结果,其中两人恰好选择同一种支付方式的有3种,
∴两人恰好选择同一种支付方式的概率为.
19.(1);(2)证明见解析.
【解析】
(1)由为内心,可得,从而可得答案;
(2)连接,,,结合(1)可得,,,四点共圆,先证明,进而可得结论.
【详解】
(1)因为为内心,所以,
,,
则.
(2)证明:连接,,,由(1)知,
由,可得,,,四点共圆,
所以,,
又因为,所以,所以.
【点睛】
关键点点睛:解答(1)的关键是利用内心的性质可得,,解答(2)的关键是证明,,,四点共圆,得到.
20.(1)
(2)答案见解析
【解析】
【分析】
(1)代入,然后根据交、并、补集进行计算.
(2)选①,可知,分,计算;选②可知,分,计算即可;选③,分,计算.
(1)
当时,集合,,
∴或,
所以;
(2)
若选择①,则,因为,
时,,即,;
时,
所以实数a的取值范围是.
若选择②,“”是“”的充分不必要条件,则,
因为,时,,即,;
时,;
所以实数a的取值范围是.
若选择③,,因为,
时,,即,;
时,或,解得
所以实数a的取值范围是或.
21.(1)x=1或x=-3;(2)或.
【解析】
(1)将方程因式分解,即可求出方程的解;
(2)去分母,再解一元二次方程,再代入检验即可;
【详解】
(1)因为,所以,解得或
(2)解:
且,整理得即故或,经检验或均满足分母不为零,故方程的解为或;
22.(1);(2).
【解析】
【分析】
(1)设,由得,即,代入中,化简整理即可得到值,从而得到函数解析式.
(2)由(1)可得,讨论对称轴和区间的关系,利用函数单调性求得最值,即可得到所求的值.
【详解】
(1)设,由,
∴,∴,
∵,∴,
∴∴,
∴.
(2)由(1)可得
①当时,在上单增,,解得;
②当时,在上单减,在上单增,
,解得,又,故.
③当时,在上单减,,,
解得,不合题意.
综上,存在实数符合题意.
【点睛】
本题考查利用待定系数法求函数解析式,考查已知二次函数在区间的最值求参数问题,考查分析能力和计算能力,属于基础题.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.把多项式分解因式,结果是( )
A. B.
C. D.
2.如图,、、是同一平面内的三条平行直线,与间的距离是1,与间的距离是2,正三角形的三顶点分别在、、上,则的边长是( )
A. B. C. D.
3.如图,将一个含有45°角的直角三角板摆放在矩形上,若∠1=25°,则∠2的度数为( )
A.70° B.75° C.80° D.85°
4.南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积术”,其求法是:“以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,为实;一为从隅,开平方得积.”若把以上这段文字写成公式,即,其中、、是内角、、的对边.若,,则的面积为( )
A. B. C. D.
5.若集合中有且仅有一个元素,则实数的值为( )
A. B. C. D.
6.设集合,且,则( )
A. B. C.1 D.2
7.在△中,是上的点,平分,,则( )
A. B. C. D.
8.已知命题,,则命题的否定为
A., B.,
C., D.,
二、多选题
9.下列函数中,最小值为2的是
A.
B.
C.
D.
10.下列说法中正确的是( )
A.两条对角线互相垂直且平分的四边形是菱形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直、平分且相等的四边形是正方形
D.两条对角线互相平分的四边形是平行四边形
11.下列结论错误的有
A.两个不等式与成立的条件是相同的
B.已知,则的最大值为5
C.函数的最小值等于4
D.且是的充要条件
12.如图是二次函数图象的一部分,图象过点,且对称轴为,则以下选项中正确的为( )
A. B. C. D.
三、填空题
13.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若,则该矩形的面积为___________.
14.如图,小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m.已知DE=30cm,EF=20cm,那么树AB的高度等于___________m.
15.已知集合,用列举法表示集合______.
四、双空题
16.若“”是“”的充分条件,则实数的取值范围为_________;若“”是“”的充分条件但“”不是“”的必要条件, 则实数的取值范围为_________.
五、解答题
17.(1)先化简再求值:,其中a=,b=.
(2)
18.数学兴趣小组设计了一份“你最喜欢的支付方式”的调查问卷(每人必选且只能选一种支付方式),在某商场随机调查了部分顾客,并将统计结果绘制成如下所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)将条形统计图补充完整,在扇形统计图中表示“现金”支付的扇形圆心角的度数为多少?
(2)若之前统计遗漏了15份问卷,已知这15份问卷都是采用“支付宝”进行支付,问重新统计后的众数所在的分类与之前统计的情况是否相同,并简要说明理由;
(3)在一次购物中,嘉嘉和琪琪随机从“微信,支付宝,银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
19.如图所示,点为的内切圆圆心,直线,分别与内切圆切于点,,且直线交直线于点.
(1)若,求的度数;
(2)求证:.
20.在①;②“”是“”的充分不必要条件;③这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.
问题:已知集合,.
(1)当时,求;
(2)若______,求实数a的取值范围.
21.解方程
(1)x2+2x-3=0;
(2).
22.若二次函数满足且.
(1)求的解析式;
(2)是否存在实数,使函数的最小值为2?若存在,求出的值;若不存在,说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
先利用分组分解法得,再利用平方差公式分解因式即可
【详解】
解:,
故选:B
2.D
【解析】
【详解】
作高AE,BG,CF(如图),
设AD=x,则AC=3x,
于是,,
∵∠BDG=∠CDF,
∠BGD=∠CFD=90°,
∴Rt△BDG∽Rt△CDF,
,即,
.
故选:D.
3.A
【解析】
【分析】
直角利用三角形外角的性质,结合平行四边形的性质,即可求解.
【详解】
由题意,因为,,所以,
又因为矩形对边平行,所以,
故选:A
4.A
【解析】
【分析】
利用余弦定理以及题中等式可求得的面积.
【详解】
由余弦定理可得,所以,,
所以,.
故选:A.
5.C
【解析】
【分析】
讨论与方程有一实根即可求解.
【详解】
当时,,符合题意;
当时,有一实根,所以,符合题意;
所以实数的值为或
故选:C
6.D
【解析】
【分析】
求得集合和,根据题意,得到,即可求解.
【详解】
解:由题意,集合,,
因为,可得,解得.
故选:D.
7.C
【解析】
【分析】
过点作,延长与交于点,可证明△∽△,结合平分,可得,,从而可知.
【详解】
过点作,延长与交于点,
则,所以△∽△,且,
又因为平分,所以,
故△是等腰三角形,且,
所以.
故选:C.
【点睛】
本题考查角分线、相似三角形的性质,考查学生的推理能力,属于基础题.
8.A
【解析】
【分析】
根据全程命题的否定是特称命题,这一规则书写即可.
【详解】
全称命题“,”的否定为特称命题,故命题的否定为“,”.
故答案为A.
【点睛】
这个题目考查了全称命题的否定的写法,换量词否结论,不变条件.
9.AB
【解析】
对A,根据二次函数的最值判定即可.
对B,利用基本不等式判定即可.
对C,利用基本不等式判定即可.
对D,根据指数函数的值域判定即可.
【详解】
对A, ,当且仅当时取等号.故A正确.
对B, ,当且仅当时取等号.故B正确.
对C, .取等号时,又故不可能成立.故C错误 .
对D,因为,故.故D错误.
故选:AB
【点睛】
本题主要考查了函数最值的运算,属于基础题.
10.ACD
【解析】
【分析】
利用菱形的判定,矩形的判定,正方形的判定依次判断可求解.
【详解】
对于选项A,两条对角线互相垂直且平分的四边形是菱形,故A说法正确;
对于选项B,两条对角线相等的平行四边形是矩形,故B说法错误;
对于选项C,两条对角线互相垂直、平分且相等的四边形是正方形,故C说法正确;
对于选项D,两条对角线互相平分的四边形是平行四边形,故D说法正确;
故选:ACD.
11.ABCD
【解析】
根据基本不等式等号成立的条件,重要不等式、基本不等式的应用条件逐项分析即可.
【详解】
A中成立条件为,成立条件为,故不正确;
B中, 因为,所以,最大值不是5,错误;
C中,,故,当且仅当时,等号成立,故等号取不到,错误;
D中,当且时,,当且仅当时等号成立,取时,不能得到且,故且是的充分不必要条件,故错误.
故选:ABCD
【点睛】
本题主要考查了重要不等式、基本不等式的成立条件,应用基本不等式求最值的等号成立条件,属于中档题.
12.AD
【解析】
【分析】
由抛物线的开口方向,对称轴,及特殊点代入可判断选项.
【详解】
A:∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴,即,故A正确;
B:∵对称轴为,
∴,即,故B错误;
C:由图象可知当时,,即,故C错误;
D:∵把代入解析式可得,
两式相加整理可得,
又当时,,
则,故D正确.
故选:AD.
【点睛】
二次函数的相关量判断:开口方向、对称轴、根的判别式、零点是常用的切入点.
13.12
【解析】
设小正方形的边长为,在中由勾股定理得,则可求出面积.
【详解】
设小正方形的边长为,
,,
在中,,
即,即,
则该矩形的面积为.
故答案为:12.
14.5.4
【解析】
【分析】
由题意,由此得线段之间的比例关系,建立方程组,解之可得答案.
【详解】
解:根据题意得,所以,又,所以,解得,
又,所以m,
故答案为:5.4.
15.0,1,
【解析】
【分析】
先由x的范围推出y的范围,然后从中取整数即可.
【详解】
因为,,即,
又,,,,,,,
故答案为0,1,
【点睛】
本题考查了集合的表示法属基础题.
16.
【解析】
【分析】
根据充分条件以及必要条件的定义集合的包含关系得出实数的取值范围.
【详解】
∵若“”是“”的充分条件,∴,∴
∵若“”是“”的充分条件但“”不是“”的必要条件,
∴,∴
故答案为:,
【点睛】
关键点睛:解决本题的关键在于将充分条件以及必要条件的问题转化为集合的包含关系,由集合的知识进行求解.
17.(1);(2)5.
【解析】
【分析】
(1)先根据分式混合运算的法则把原式进行化简,再把的值代入进行计算即可;
(2)指数幂的运算法则和绝对值的含义,即可求出结果.
【详解】
(1)原式=
;
当时,
,
,
∴原式.
(2).
18.(1)条形统计图见解析,;(2)不同,理由见解析;(3).
【解析】
【分析】
(1)由两幅图可知,用现金、支付宝、其他支付共有人数110人,所占比例为1-15%-30%=55%,可得共调查了多少人,再根据用银行卡、微信支付的百分比可得答案
(2)根据原数据的众数所在的分类为微信,加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝可得答案;
(3)将微信记为A、支付宝记为B、银行卡记为C,画出树状图根据古典概型概率计算公式可得答案.
【详解】
(1)由条形统计图可知,用现金、支付宝、其他支付共有人数110人,
所占比例为1-15%-30%=55%,所以共调查了人,
所以用银行卡支付的人有人,用微信支付的人有人,
用现金支付所占比例为,所以,在扇形统计图中表示“现金”支付的扇形圆心角的度数为90°,
补全统计图如图所示:
(2)重新统计后的众数所在的分类与之前统计的情况不同,理由如下:原数据的众数所在的分类为微信,而加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝.
(3)将微信记为A、支付宝记为B、银行卡记为C,画树状图如下:
∵共有9种等可能的结果,其中两人恰好选择同一种支付方式的有3种,
∴两人恰好选择同一种支付方式的概率为.
19.(1);(2)证明见解析.
【解析】
(1)由为内心,可得,从而可得答案;
(2)连接,,,结合(1)可得,,,四点共圆,先证明,进而可得结论.
【详解】
(1)因为为内心,所以,
,,
则.
(2)证明:连接,,,由(1)知,
由,可得,,,四点共圆,
所以,,
又因为,所以,所以.
【点睛】
关键点点睛:解答(1)的关键是利用内心的性质可得,,解答(2)的关键是证明,,,四点共圆,得到.
20.(1)
(2)答案见解析
【解析】
【分析】
(1)代入,然后根据交、并、补集进行计算.
(2)选①,可知,分,计算;选②可知,分,计算即可;选③,分,计算.
(1)
当时,集合,,
∴或,
所以;
(2)
若选择①,则,因为,
时,,即,;
时,
所以实数a的取值范围是.
若选择②,“”是“”的充分不必要条件,则,
因为,时,,即,;
时,;
所以实数a的取值范围是.
若选择③,,因为,
时,,即,;
时,或,解得
所以实数a的取值范围是或.
21.(1)x=1或x=-3;(2)或.
【解析】
(1)将方程因式分解,即可求出方程的解;
(2)去分母,再解一元二次方程,再代入检验即可;
【详解】
(1)因为,所以,解得或
(2)解:
且,整理得即故或,经检验或均满足分母不为零,故方程的解为或;
22.(1);(2).
【解析】
【分析】
(1)设,由得,即,代入中,化简整理即可得到值,从而得到函数解析式.
(2)由(1)可得,讨论对称轴和区间的关系,利用函数单调性求得最值,即可得到所求的值.
【详解】
(1)设,由,
∴,∴,
∵,∴,
∴∴,
∴.
(2)由(1)可得
①当时,在上单增,,解得;
②当时,在上单减,在上单增,
,解得,又,故.
③当时,在上单减,,,
解得,不合题意.
综上,存在实数符合题意.
【点睛】
本题考查利用待定系数法求函数解析式,考查已知二次函数在区间的最值求参数问题,考查分析能力和计算能力,属于基础题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
