人教版七年级上册3.1.2 等式的性质 课件 (共21张PPT)
文档属性
| 名称 | 人教版七年级上册3.1.2 等式的性质 课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 436.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
人教版七年级上册第三章 一元一次方程
3.1.2 等式的性质
一、复习引入
1、相反数
+5的相反数是几? -8的相反数是几
互为相反数的两数相加等于0
2、倒数
5的倒数是几?
互为倒数的两数相乘得1.
二、温故知新
(1)x + 1=3
(2)
2、什么是等式?请举几个等式的例子。
实际问题
一元一次方程
设未知数
列方程
(3)
3、小学我们学习过等式性质是怎样描述的?
1、
4x=24
三、探究新知
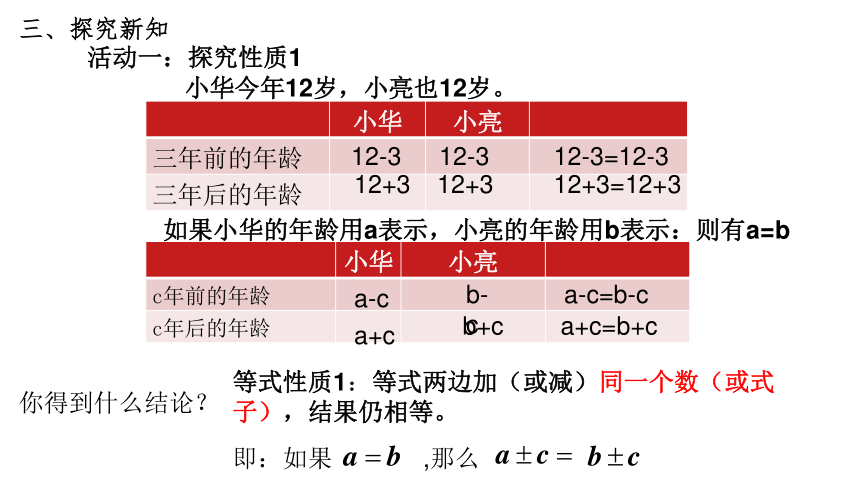
活动一:探究性质1
小华今年12岁,小亮也12岁。
小华 小亮
三年前的年龄
三年后的年龄
12-3
12-3
12+3
12+3
12-3=12-3
12+3=12+3
小华 小亮
c年前的年龄
c年后的年龄
如果小华的年龄用a表示,小亮的年龄用b表示:则有a=b
a-c
b-c
a+c
b+c
a-c=b-c
a+c=b+c
你得到什么结论?
等式性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
即:如果 ,那么
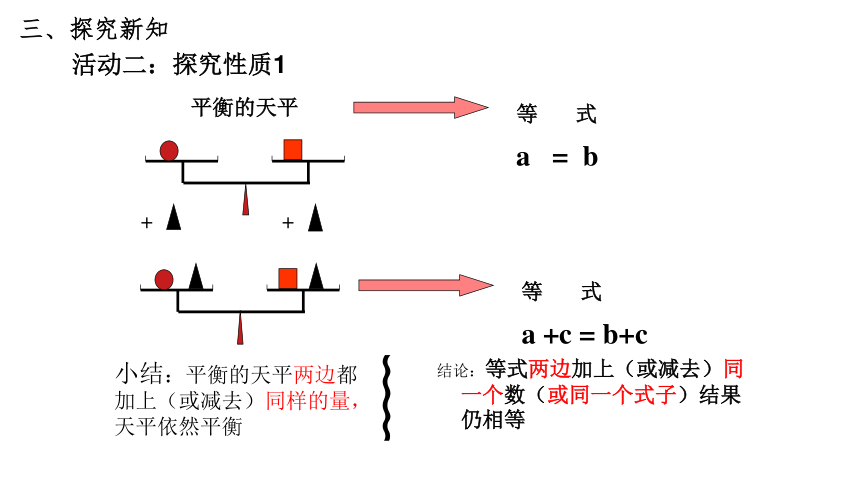
等 式
a = b
+ +
平衡的天平
等 式
a +c = b+c
小结:平衡的天平两边都
加上(或减去)同样的量,
天平依然平衡
结论:等式两边加上(或减去)同一个数(或同一个式子)结果仍相等
︴
活动二:探究性质1
三、探究新知
请你思考:乘和除也具有这样的等式性质吗?
+ - × ÷
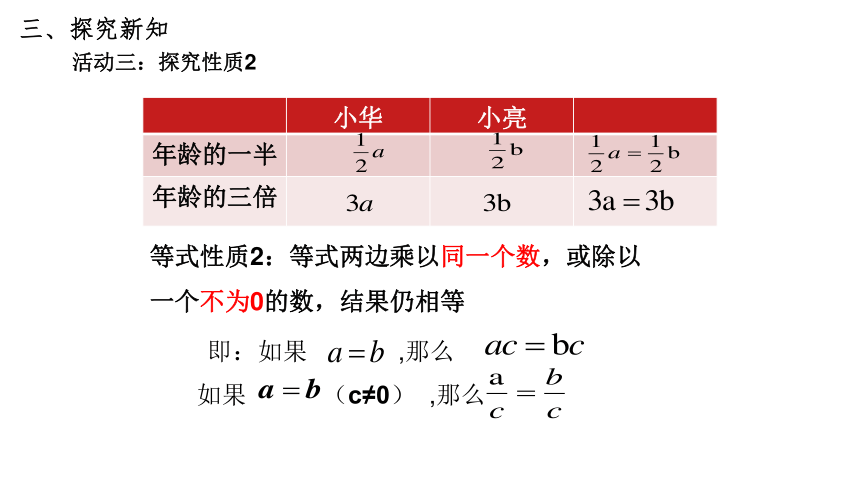
小华 小亮
年龄的一半
年龄的三倍
等式性质2:等式两边乘以同一个数,或除以一个不为0的数,结果仍相等
即:如果 ,那么
如果 (c≠0) ,那么
活动三:探究性质2
三、探究新知
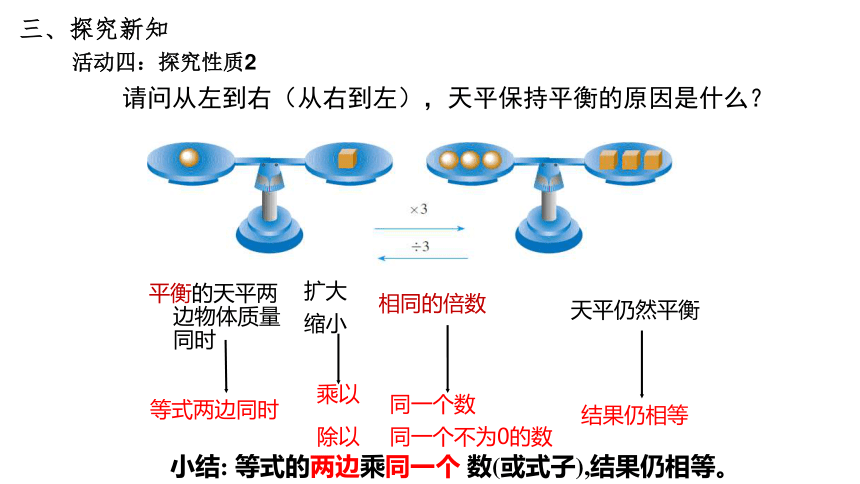
平衡的天平两边物体质量同时
扩大
缩小
相同的倍数
天平仍然平衡
等式两边同时
乘以
除以
同一个数
结果仍相等
请问从左到右(从右到左),天平保持平衡的原因是什么?
同一个不为0的数
活动四:探究性质2
三、探究新知
小结: 等式的两边乘同一个 数(或式子),结果仍相等。
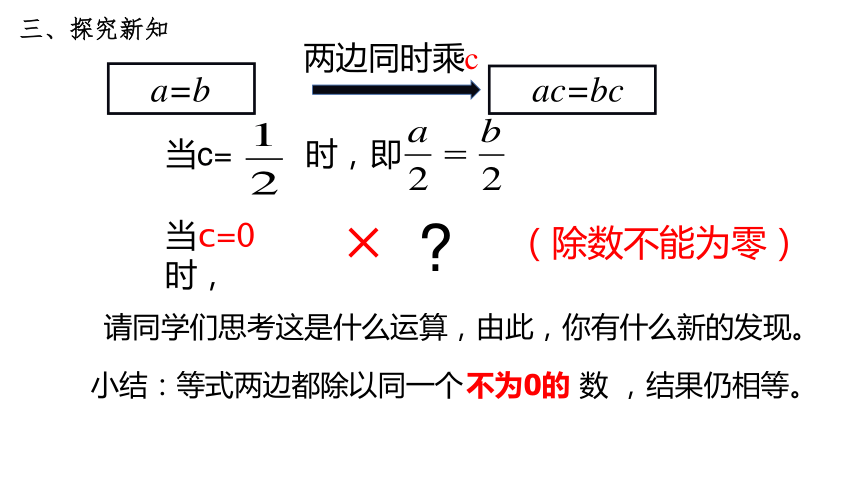
ac=bc
a=b
当c= 时,即
请同学们思考这是什么运算,由此,你有什么新的发现。
小结:等式两边都除以同一个 数 ,结果仍相等。
当c=0 时,
(除数不能为零)
不为0的
两边同时乘c
三、探究新知
等式性质1:如果a=b,
那么 a±c=b±c
等式性质2 :如果a=b,那么ac=bc
如果a=b (c≠0),那么
①原式是等式
②加减同一个数(或式)
③结果是等式
①原式是等式
②乘同一个数
③ 除同一个不为0的数
④结果是等式
用等式的性质解方程.
解:两边加5,得
化简,得
两边乘(-3),得
x=-27是原方程的解吗?
注意①两边必须同时进行同一种计算;②加(或减或乘或除以同一个不为零)的数时必须是同一个数或同一个式子.
(把方程化为x=a的形式)
三、探究新知
下列从左边到右边的变形正确吗?说明理由.
(1)若 x = y , 那么x + 2 = y - 2.
(2)若 x = y , 那么 .
(3)若 2m - 3 = 0 , 那么2m = 3.
(4)若 -3x =-3 y , 那么x = y .
×
×
√
√
四、感受变形 体会作用
利用等式的性质解下列方程:
(1) x + 1=3
(2) 4x=24
(3)
解方程的目的就是化简方程求出未知数x的值
x = a
一般的,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等。
五、感受化简 体会作用
.
解方程的目的是求出未知数x的值
x = a
练习:利用等式的性质解下列方程
(1)x-5= 6 (2)5 x+4=0
(3)0.3 x =45
(4)
六、熟练应用 体会作用
等式的变形: 3a+b-2=7a+b-2
过程如下:
3a+b=7a+b
3a=7a
3=7
3怎么和7相等了?
聪明的你,知道是什么原因吗?
乏腔音绽俏勾意婪挂荣杯丢呸谤禁拈语校疫斑良吓抨撬壬桥女互油纬引佰人教版七年级上册数学《等式的性质》课件人教版七年级上册数学《等式的性质》课件
思考
一、等式的
性质:
等式两边同时,加、减、乘、除以(不为0)同一个数,结果仍相等。
运用等式的性质把方程“转化”为 x = a(a为常数) 的形式.
二、等式的性质的应用:
三、渗透的数学思想:
1.构建等量关系的数学模型的思想.
2.渗透化归的数学思想.
七、课堂小结
请以《我是等式》为题,写一段自我介绍,阐述等式的定义、性质和作用等。
学习三问:
为什么学习它?
怎样学习它?
学习它有什么用?
七、总结体会 感悟收获
练习一:快速选出正确的答案.
1、下列运用等式的性质进行变形,正确的( )
A、若x=y,则x-5=y+5
B、若ac=bc,则a=b
C、
D、 若x=y,则
c
八、随堂练习
练习二:用等式的性质解下列方程并检验:
(1)x-5=6 (2)0.3x=45 (3)5x+4=0
检验:当 时,左边=0=右边,
所以 是原方程的解。
解;(3)两边减4,得
化简,得
两边除以5,得
作业一:课本P83习题1.3复习巩固3、4题.
作业二(选作题):
已知 ,你能求出 的值吗?
(提示:先用等式的性质求出 )
九、布置作业
谢谢聆听
人教版七年级上册第三章 一元一次方程
3.1.2 等式的性质
一、复习引入
1、相反数
+5的相反数是几? -8的相反数是几
互为相反数的两数相加等于0
2、倒数
5的倒数是几?
互为倒数的两数相乘得1.
二、温故知新
(1)x + 1=3
(2)
2、什么是等式?请举几个等式的例子。
实际问题
一元一次方程
设未知数
列方程
(3)
3、小学我们学习过等式性质是怎样描述的?
1、
4x=24
三、探究新知
活动一:探究性质1
小华今年12岁,小亮也12岁。
小华 小亮
三年前的年龄
三年后的年龄
12-3
12-3
12+3
12+3
12-3=12-3
12+3=12+3
小华 小亮
c年前的年龄
c年后的年龄
如果小华的年龄用a表示,小亮的年龄用b表示:则有a=b
a-c
b-c
a+c
b+c
a-c=b-c
a+c=b+c
你得到什么结论?
等式性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
即:如果 ,那么
等 式
a = b
+ +
平衡的天平
等 式
a +c = b+c
小结:平衡的天平两边都
加上(或减去)同样的量,
天平依然平衡
结论:等式两边加上(或减去)同一个数(或同一个式子)结果仍相等
︴
活动二:探究性质1
三、探究新知
请你思考:乘和除也具有这样的等式性质吗?
+ - × ÷
小华 小亮
年龄的一半
年龄的三倍
等式性质2:等式两边乘以同一个数,或除以一个不为0的数,结果仍相等
即:如果 ,那么
如果 (c≠0) ,那么
活动三:探究性质2
三、探究新知
平衡的天平两边物体质量同时
扩大
缩小
相同的倍数
天平仍然平衡
等式两边同时
乘以
除以
同一个数
结果仍相等
请问从左到右(从右到左),天平保持平衡的原因是什么?
同一个不为0的数
活动四:探究性质2
三、探究新知
小结: 等式的两边乘同一个 数(或式子),结果仍相等。
ac=bc
a=b
当c= 时,即
请同学们思考这是什么运算,由此,你有什么新的发现。
小结:等式两边都除以同一个 数 ,结果仍相等。
当c=0 时,
(除数不能为零)
不为0的
两边同时乘c
三、探究新知
等式性质1:如果a=b,
那么 a±c=b±c
等式性质2 :如果a=b,那么ac=bc
如果a=b (c≠0),那么
①原式是等式
②加减同一个数(或式)
③结果是等式
①原式是等式
②乘同一个数
③ 除同一个不为0的数
④结果是等式
用等式的性质解方程.
解:两边加5,得
化简,得
两边乘(-3),得
x=-27是原方程的解吗?
注意①两边必须同时进行同一种计算;②加(或减或乘或除以同一个不为零)的数时必须是同一个数或同一个式子.
(把方程化为x=a的形式)
三、探究新知
下列从左边到右边的变形正确吗?说明理由.
(1)若 x = y , 那么x + 2 = y - 2.
(2)若 x = y , 那么 .
(3)若 2m - 3 = 0 , 那么2m = 3.
(4)若 -3x =-3 y , 那么x = y .
×
×
√
√
四、感受变形 体会作用
利用等式的性质解下列方程:
(1) x + 1=3
(2) 4x=24
(3)
解方程的目的就是化简方程求出未知数x的值
x = a
一般的,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等。
五、感受化简 体会作用
.
解方程的目的是求出未知数x的值
x = a
练习:利用等式的性质解下列方程
(1)x-5= 6 (2)5 x+4=0
(3)0.3 x =45
(4)
六、熟练应用 体会作用
等式的变形: 3a+b-2=7a+b-2
过程如下:
3a+b=7a+b
3a=7a
3=7
3怎么和7相等了?
聪明的你,知道是什么原因吗?
乏腔音绽俏勾意婪挂荣杯丢呸谤禁拈语校疫斑良吓抨撬壬桥女互油纬引佰人教版七年级上册数学《等式的性质》课件人教版七年级上册数学《等式的性质》课件
思考
一、等式的
性质:
等式两边同时,加、减、乘、除以(不为0)同一个数,结果仍相等。
运用等式的性质把方程“转化”为 x = a(a为常数) 的形式.
二、等式的性质的应用:
三、渗透的数学思想:
1.构建等量关系的数学模型的思想.
2.渗透化归的数学思想.
七、课堂小结
请以《我是等式》为题,写一段自我介绍,阐述等式的定义、性质和作用等。
学习三问:
为什么学习它?
怎样学习它?
学习它有什么用?
七、总结体会 感悟收获
练习一:快速选出正确的答案.
1、下列运用等式的性质进行变形,正确的( )
A、若x=y,则x-5=y+5
B、若ac=bc,则a=b
C、
D、 若x=y,则
c
八、随堂练习
练习二:用等式的性质解下列方程并检验:
(1)x-5=6 (2)0.3x=45 (3)5x+4=0
检验:当 时,左边=0=右边,
所以 是原方程的解。
解;(3)两边减4,得
化简,得
两边除以5,得
作业一:课本P83习题1.3复习巩固3、4题.
作业二(选作题):
已知 ,你能求出 的值吗?
(提示:先用等式的性质求出 )
九、布置作业
谢谢聆听
