人教A版2019选择性必修第二册5.3.1 函数的单调性 同步练习(Word版含解析)
文档属性
| 名称 | 人教A版2019选择性必修第二册5.3.1 函数的单调性 同步练习(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 15:16:50 | ||
图片预览



文档简介
第五章:一元函数的导数及其应用
5.3 导数在研究函数中的应用
5.3.1 函数的单调性
【题型归纳】
题型一:利用导数求函数的单调性(不含参)
1.(2021·广西河池·高二月考(理))函数在上的单调减区间为( )
A. B. C. D.
2.(2021·全国·高二单元测试)已知函数f(x)与其导函数f'(x)的图象如图所示,则函数g(x)=的单调递减区间为( )
A.(0,1)和(4,+∞) B.(0,2)
C.(﹣∞,0)和(1,4) D.(0,3)
3.(2021·陕西·绥德中学高二月考(理))若曲线在点处的切线过点,则函数的单调递减区间为( )
A. B.
C. D.,
题型二:由函数的单调性求参数
4.(2021·广东·东莞市光明中学高二月考)若在上是减函数,则的取值范围是( )
A. B.
C. D.
5.(2021·陕西·渭南市尚德中学高二月考(理))已知在R上是增加的,则的取值范围是( )
A. B. C.或 D.或
6.(2021·山东·兰陵四中高二期中)若函数在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
题型三:由函数在区间的单调性求参数
7.(2021·重庆市清华中学校高二月考)若函数在区间内存在单调递增区间,则实数的取值范围是( )
A. B. C. D.
8.(2021·全国·高二课时练习)已知函数在上为减函数,则实数a的取值范围是( )
A. B. C. D.
9.(2021·河南·高二期末(理))若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
题型四:函数与导函数图像的关系
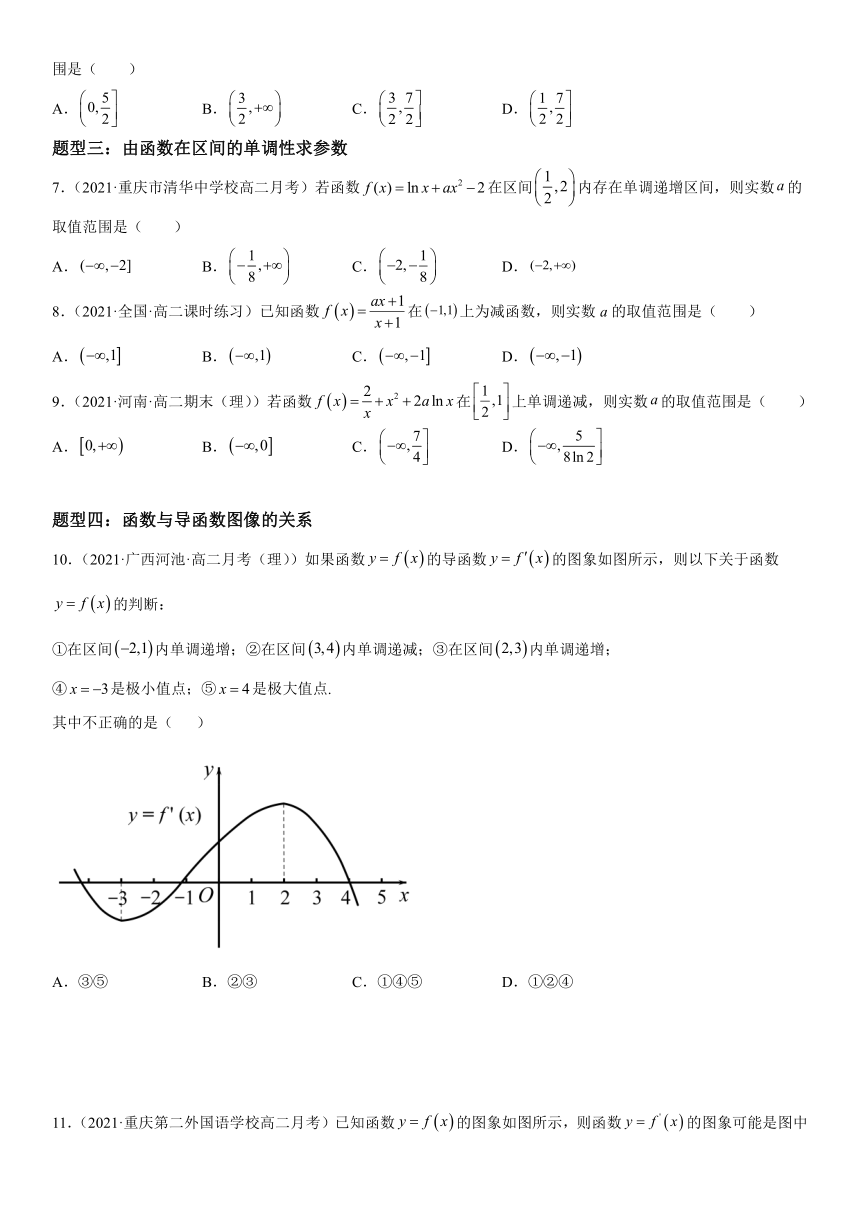
10.(2021·广西河池·高二月考(理))如果函数的导函数的图象如图所示,则以下关于函数的判断:
①在区间内单调递增;②在区间内单调递减;③在区间内单调递增;
④是极小值点;⑤是极大值点.
其中不正确的是( )
A.③⑤ B.②③ C.①④⑤ D.①②④
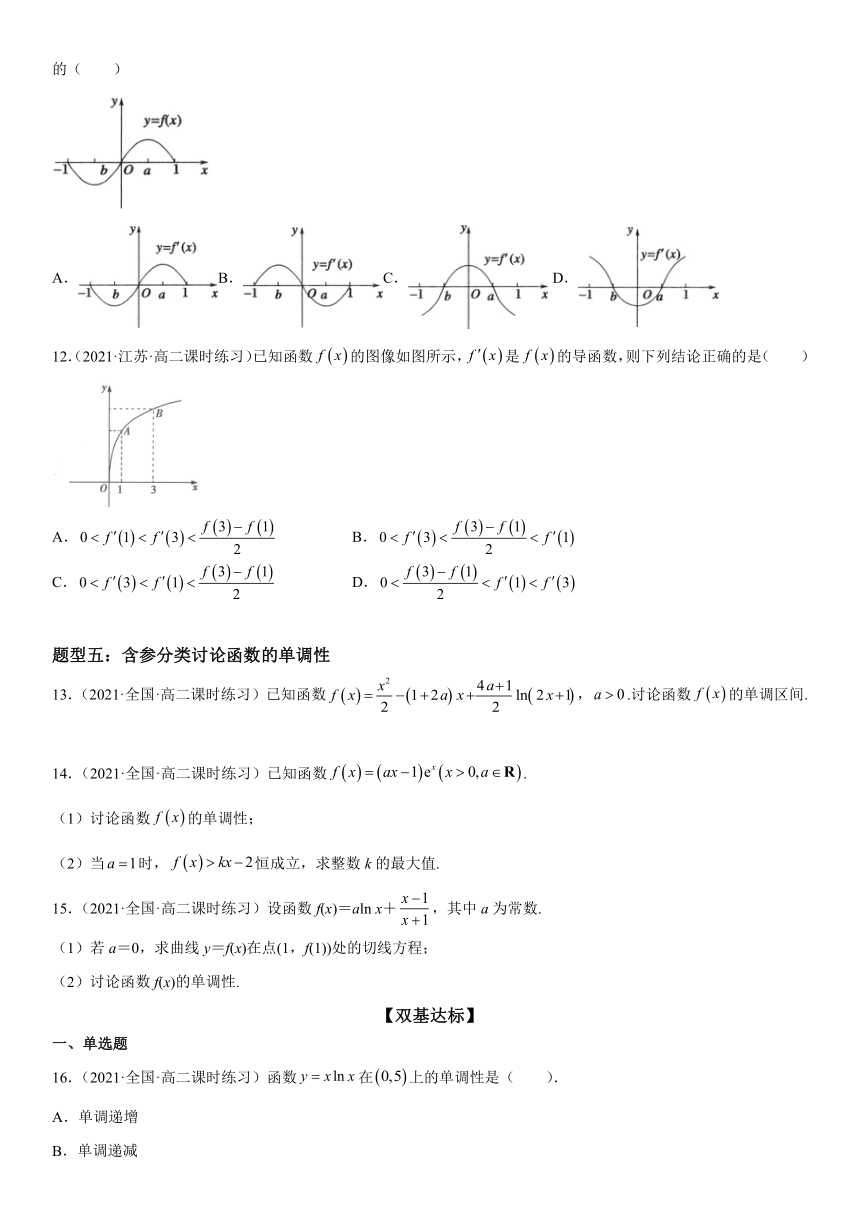
11.(2021·重庆第二外国语学校高二月考)已知函数的图象如图所示,则函数的图象可能是图中的( )
A.B.C. D.
12.(2021·江苏·高二课时练习)已知函数的图像如图所示,是的导函数,则下列结论正确的是( )
A. B.
C. D.
题型五:含参分类讨论函数的单调性
13.(2021·全国·高二课时练习)已知函数,.讨论函数的单调区间.
14.(2021·全国·高二课时练习)已知函数.
(1)讨论函数的单调性;
(2)当时,恒成立,求整数k的最大值.
15.(2021·全国·高二课时练习)设函数f(x)=aln x+,其中a为常数.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
【双基达标】
一、单选题
16.(2021·全国·高二课时练习)函数在上的单调性是( ).
A.单调递增
B.单调递减
C.在上单调递减,在上单调递增
D.在上单调递增,在上单调递减
17.(2021·全国·高二课时练习)已知函数的导函数有下列信息:
①时,;
②时,或;
③时,或.
则函数的大致图像是图中的( ).
A. B.
C. D.
18.(2021·广西河池·高二月考(理))定义在上的函数其导函数恒成立,且,则不等式的解集为( )
A. B. C. D.
19.(2021·河北承德第一中学高二月考)在上可导的函数的图象如图所示,则关于的不等式的解集为( )
A. B.
C. D.
20.(2021·全国·高二单元测试)定义域为R的函数且,且的导函数,则实数a的取值范围为( )
A. B. C. D.
21.(2021·全国·高二单元测试)已知函数,则在上不单调的一个充分不必要条件是( )
A. B.
C. D.
22.(2021·江苏·高二课时练习)已知函数的导函数为,对任意的实数都有,,则不等式的解集是( )
A. B. C. D.
23.(2021·新疆维吾尔自治区喀什第二中学高二期中)设f'(x)是函数f(x)的导函数,若f'(x)>0,且 x1,x2∈R(x1≠x2),f(x1)+f(x2)<2f(),则下列各项中不一定正确的是( )
A.f(2)<f(e)<f(π)
B.f′(π)<f′(e)<f′(2)
C.f(2)<f′(2)﹣f′(3)<f(3)
D.f′(3)<f(3)﹣f(2)<f′(2)
24.(2021·全国·高二专题练习)设函数是偶函数的导数, ,当时, ,则使|f(x)|>成立的x的取值范围是( )
A. B.
C. D.
25.(2021·全国·高二专题练习)定义在R上的偶函数,其导函数,当x≥0时,恒有,若,则不等式的解集为( )
A.(,1) B.(∞,)∪(1,+∞)
C.(,+∞) D.(∞,)
【高分突破】
一:单选题
26.(2021·江苏·南京市中华中学高二期中)已知函数在区间,上是单调增函数,则实数的取值范围为( )
A. B. C. D.
27.(2021·江西·景德镇一中高二期中)函数的图象大致是( )
A. B.
C. D.
28.(2021·全国·高二单元测试)设为实数,函数,且是偶函数,则的单调递增区间为( )
A. B.,
C. D.
29.(2021·广西·蒙山中学高二月考(理))已知定义在R上的函数f(x)满足f(2)=20,且f(x)的导函数满足,则不等式f(x)>2x3+2x的解集为( )
A.{x|x>-2} B.{x|x>2} C.{x|x<2} D.{x|x<-2或x>2}
30.(2021·江苏·高二课时练习)已知函数及其导函数满足且.若恒成立,则( )
A. B.
C. D.
31.(2021·北京一七一中高二月考)已知函数,且,则下列叙述正确的是( )
A. B.
C. D.
32.(2021·全国·高二课时练习)已知定义在上的函数满足对,其中是函数的导函数,若,则实数的取值范围为( )
A. B.
C. D.
33.(2021·全国·高二课时练习)若函数在区间上不是单调函数,则实数的取值范围是( )
A. B.
C. D.不存在这样的实数
34.(2021·浙江·临海市西湖双语实验学校高二月考)设分别是定义在上的偶函数和奇函数,为其导函数.当时,且.则使得不等式成立的的取值范围是( )
A. B.
C. D.
二、多选题
35.(2021·重庆十八中高二月考)已知函数,则( )
A.在定义域内单调性不变 B.在定义域内有零点
C.的导数在定义域内单调性不变 D.为奇函数
36.(2021·全国·高二单元测试)已知函数,,是其导函数,恒有,则( )
A. B.
C. D.
37.(2021·江苏省苏州第十中学校高二月考)已知是定义在R上函数,是的导数,则以下说法正确的是( )
A.若,则;
B.当时,可,则;
C.当时,可,且,则;
D.若,且,则的解集为
38.(2021·广东茂名·高二期末)已知函数是定义在上的可导函数,其导函数为,若,且,则使不等式成立的的值不可能为( )
A. B. C. D.
39.(2020·广东·广州市协和中学高二期中)已知函数,若关于的方程有4个不同的实数根,则实数的取值可以为( )
A. B. C. D.
三、填空题
40.(2021·浙江杭州·高二期中)已知函数在上是增函数,则实数的取值范围是__.
41.(2021·全国·高二课时练习)函数y=f(x)在其定义域内可导,其图象如图所示,记y=f(x)的导函数为y=,则不等式≤0的解集为________.
42.(2021·全国·高二单元测试)已知奇函数的导函数为,,若,则实数的取值范围为______.
43.(2021·江西上饶·高二月考(理))已知函数,则以下结论正确的是___________.
①在R上单调递增
②
③方程有实数解
④存在实数k,使得方程有4个实数解
四、解答题
44.(2021·全国·高二课时练习)求下列函数的单调区间:
(1)f(x)=2x3+3x2-36x+1;
(2)f(x)=sin x-x(045.(2021·山东任城·高二期中)已知函数.
(1)当时,求的单调区间;
(2)若在区间上单调递增,求的取值范围.
46.(2021·江苏·无锡市第一中学高二期中)已知函数,其中为正实数.
(1)试讨论函数的单调性;
(2)设,若存在,,使得不等式成立,求的取值范围.
47.(2021·全国·高二课时练习)已知函数,,.
(1)若函数在上单调递减,求实数a的取值范围;
(2)若函数存在单调递减区间,求实数a的取值范围.
48.(2021·河南·辉县市第一高级中学高二月考(理))已知函数的图象过点,若关于的方程有3个不同的实数根,
(1)求函数的单调区间;
(2)求的取值范围.
【答案详解】
1.C
【分析】
求导,令导函数小于零,解不等式即可
【详解】
解:由已知
令,且
则,
即单调减区间为
故选:C.
2.A
【分析】
结合函数图象,求出f′(x)﹣f(x)<0成立的x的范围即可.
【详解】
根据导函数和函数的关系可判断两函数如图:
结合图象:x∈(0,1)和x∈(4,+∞)时,f′(x)﹣f(x)<0,
所以,
故g(x)在(0,1),(4,+∞)递减,
故选:A
3.D
【分析】
先利用导数求出函数在处的切线方程,然后将点代入切线方程,即可求出的值,最后利用导数的符号大于零即可求解.
【详解】
由题意得,
所以,且.
故函数在,处的切线为:
,将点代入得.
则,由得且.
故的单调递减区间为,.
故选:D.
4.C
【分析】
先求,再将在上是减函数,转化为在上恒成立,而后分离参数求在上的最小值,可得实数的取值范围.
【详解】
由题知,,.
若在上是减函数,则在上恒成立,
由得,,
当时,,
所以.
故选:C.
5.B
【分析】
由题意得函数的导数大于等于0,可得在上恒成立,利用一元二次函数的图象,即可得到答案;
【详解】
由题意得函数的导数大于等于0,可得在上恒成立,
,
故选:B
6.D
【分析】
首先利用导数求函数的减区间,再利用子集关系,列式求的取值范围.
【详解】
,
当,解得:,
由条件可知,
所以 ,解得:.
故选:D
7.D
【分析】
求出函数的导数,问题转化为 而 在 递增,求出 的最小值,从而求出的范围即可 .
【详解】
若在区间内存在单调递增区间,则有解,
故
令
在递增 ,
故
故选:D
8.B
【分析】
求出导函数,将问题转化为在上恒成立,进而得出,分析不具有单调性,从而可得.
【详解】
由题意,得,又在上恒成立,所以.
而当时,恒为0,此时(),不具有单调性,
所以,即实数a的取值范围为.
故选:B
9.B
【分析】
根据函数的区间单调性,应用导数可得在上恒成立,构造并研究单调性即可求的取值范围.
【详解】
由,得,
由在上单调递减,得在上恒成立,即在上恒成立.
令,在上,
∴在上单调递减,即,
∴,故的取值范围.
故选:.
10.A
【分析】
根据导函数与单调性和极值点的关系,观察图像即可得出答案.
【详解】
由图可知,
在区间内,有正有负,①错误;
在区间内,,在区间内单调递增,②错误;
在区间内,,在区间内单调递增,③正确;
不存在,使当时,,当时,,④错误;
存在,使当时,,当时,,如,⑤正确
故选:A.
11.C
【分析】
由函数的图象的增减变化趋势,判断函数取值的正、负,由此判断可得选项.
【详解】
解:由函数的图象的增减变化趋势,判断函数取值的正、负情况如下表:
x
递减 递增 递减
所以当时,函数的图象在x轴下方;
当时,函数的图象在x轴上方;
当时,函数的图象在x轴下方.
故选:C.
12.B
【分析】
结合图象,判断出的大小关系.
【详解】
由题图可知函数的图像在处的切线的斜率比在处的切线的斜率大,且均为正数,所以.
的斜率为,其比在处的切线的斜率小,但比在处的切线的斜率大,所以.
故选:B
13.答案见解析
【分析】
求导可得,对和的大小进行分类讨论可得函数的单调区间.
【详解】
函数定义域是,
,
①当时,即时,当或时,;当时,.
此时,的增区间是和,减区间是,
②当时,对任意的恒成立,
此时,函数增区间,无减区间;
③当时,即时,当或时,;当时,.
此时,函数的增区间是和,减区间是.
综上,当时,函数的增区间是和,减区间是;
当时,函数的增区间是;
当时,函数的增区间是和,减区间是;
14.
(1)答案见解析;
(2)1.
【分析】
(1)求出函数导数后,分三种情况讨论,即可求解函数单调区间;
(2)分离参数可得对于恒成立,令,利用导数求出函数,分析出,即可求出整数k的最大值.
(1)
由得.
当时,,故在上单调递增;
当时,令,解得.
故在上单调递减,在上单调递增;
当时,,故在上单调递减.
(2)
原不等式等价于对于恒成立.
令,则.
令,则,所以在上单调递增.
又,,
所以存在,使得,
且在上单调递减,在上单调递增,
所以,
又,所以,
所以,所以,
经验证时,恒成立,所以整数k的最大值为1.
15.(1)x-2y-1=0;(2)答案见解析.
【分析】
(1)先求出的值,得出切点坐标,再求出的值,得到切线的斜率,从而得到切线方程.
(2)先求出,对二次函数的开口方向,判别式进行分类讨论即可.
【详解】
(1)由题意知a=0时,,x∈(0,+∞).
此时f′(x)=.可得f′(1)=,又f(1)=0,
所以曲线y=f(x)在(1,f(1))处的切线方程为x-2y-1=0.
(2)函数f(x)的定义域为(0,+∞),f′(x)=+=.
当a≥0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增.
当a<0时,令g(x)=ax2+(2a+2)x+a,由于=(2a+2)2-4a2=4(2a+1),
①当时,,
f′(x)=≤0,函数f(x)在(0,+∞)上单调递减.
②当时,<0,g(x)<0,f′(x)<0,函数f(x)在(0,+∞)上单调递减.
③当-时,>0.
设x1,x2(x1则x1=,x2=,
由x1==,
所以x∈(0,x1)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
x∈(x1,x2)时,g(x)>0,f′(x)>0,函数f(x)单调递增,
x∈(x2,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
综上可得:当a≥0时,函数f(x)在(0,+∞)上单调递增;
当时,函数f(x)在(0,+∞)上单调递减;
当时,函数f(x)在,上单调递减,在上单调递增.
16.C
【分析】
利用导数判断函数在上的单调性.
【详解】
,令,得;
令,得,
∴函数在上单调递减,在上单调递增.
故选:C
17.C
【分析】
根据导数的正负与函数的单调性关系判断.
【详解】
根据导函数信息知,函数在上是增函数,在,上是减函数.
故选:C.
18.C
【分析】
根据题意,设g(x)=f(x) 3x,求出其导数,分析可得g′(x)<0,则g(x)在R上为减函数,又由f(1)=3,则g(1)=0, ,结合函数的单调性分析可得答案.
【详解】
解:设g(x)=f(x) 3x,则g′(x)=f′(x) 3,
又由f′(x)<3,则g′(x)<0,则g(x)在R上为减函数,
又由f(1)=3,则g(1)=f(1) 3=0,
则g(x)过点,且在R上为减函数,
由得
即,由于过点,且在R上为增函数,
则必有
故选:C
19.A
【分析】
根据单调性导数的关系得出和的解集,然后可得题设不等式的解集.
【详解】
由题意的解集为,,的解集为,
或,所以或.
故选:A.
20.B
【分析】
由题可得函数为R上的单调递增函数,即求.
【详解】
由可知,设,
,是R上的单调递增函数.
由且,可知且,
.
故选:B.
21.D
【分析】
求出函数的导数,问题转化为函数与x轴在上有交点,即求.
【详解】
函数的定义域为,,
令,
若在上不单调,则函数与x轴在上有交点,
又,
则,
解得,
故在上不单调的一个充分不必要条件是.
故选:D.
22.C
【分析】
由已知条件构造函数,再根据,求,不等式转化为,结合函数的单调性和奇偶性,解抽象不等式.
【详解】
解:由题意得,
则
,
由,解得:,
故,
(2),
当时,,,,
在上恒成立,
即在上单调递增,
又,故为上的偶函数,
其图象关于轴对称,在上单调递减,
故,故,
故选:C.
23.C
【分析】
f′(x)>0,∴f(x)在R上单调递增,由,可得<,可得y=f(x)的图象如图所示,图象是向上凸.进而判断出正误.
【详解】
解:∵f′(x)>0,∴f(x)在R上单调递增,
∵,
∴<,
∴y=f(x)的图象如图所示,图象是向上凸.
∴f(2)<f(e)<f(π),f′(π)<f′(e)<f′(2),可知:A,B正确.
∵f(3)﹣f(2)=,表示点A(2,f(2)),B(3,f(3))的连线的斜率.
由图可知:f′(3)<kAB<f′(2),故D正确.
C项无法推出,
故选:C.
24.C
【分析】
设,根据函数的单调性和奇偶性问题转化为,求出不等式的解集即可.
【详解】
解:设F(x)=xf(x),
易知函数F(x)为奇函数,且当x<0时,F′(x)=xf′(x)+f(x)>0,
故函数F(x)在R递增,
将目标不等式转化为|F(x)|>F(1)=1,
结合函数的单调性得:|x|>1,解得:或x>1,
故不等式的解集是(﹣∞,﹣1)∪(1,+∞),
故选:C.
25.A
【分析】
由已知可得,即在上单调递减,再利用函数的奇偶性、单调性,求解题设不等式即可.
【详解】
当时,,又,
∴,即在上单调递减.
∵是定义在R上的偶函数,
∴是定义在R上的偶函数,
由不等式,则有,
∴,解得:.
∴不等式的解集为.
故选:A
26.D
【分析】
由题意得到在,恒成立,利用分离参数法和基本不等式即可求出实数的取值范围.
【详解】
解:在区间,上是单调增函数,
当,时,恒成立,
,
又(当且仅当时取等号),即,
.
故选:D.
27.A
【分析】
由函数有两个零点排除选项C,D;再借助导数探讨函数的单调性与极值情况即可判断作答.
【详解】
由得,或,选项C,D不满足;
由求导得,当或时,,当时,,
于是得在和上都单调递增,在上单调递减,在处取极大值,在处取极小值,B不满足,A满足.
故选:A
28.B
【分析】
先利用定义算出,在求导算出单调区间.
【详解】
因为,所以,
因为是偶函数,所以对恒成立,
即,即,
所以,所以,令,解得或,
所以的单调递增区间为,.
故选:B.
29.B
【分析】
根据给定条件构造函数并判断其单调性,再利用的单调性即可求出不等式f(x)>2x3+2x的解集.
【详解】
令,因,则,即在R上单调递增,
因,则不等式f(x)>2x3+2x等价于,于是得x>2,
所以原不等式的解集为{x|x>2}.
故选:B
30.D
【分析】
构造函数,通过题意,可得函数的单调区间,以及,
从而可得,再通过分离参数,即可求解.
【详解】
解:设,则,
当时,,当时,
在上单调递增,在上单调递减,
,
不等式可转化为,
该不等式恒成立,
则,
故选:D.
31.B
【分析】
根据题意,求出函数的导数,分析可得区间上为增函数,据此分析可得答案.
【详解】
根据题意,函数,其导数,
在区间上,,函数为增函数,
若,则,
故选:B.
32.D
【分析】
引入新函数,求导后确定的单调性,由单调性解不等式.
【详解】
令,,则,
因为,所以,所以函数在上单调递减.
因为,所以,所以,
即,所以且,解得,
所以实数的取值范围为.
故选:D.
【点睛】
易错点睛:应用导数研究函数的单调性、极值、最值等性质时,首先要考虑函数的定义域,即单调区间、极值点都要在函数的定义域内,本题容易因忽略而出错.
33.B
【分析】
根据题意,导函数在区间上有正有负,所以在区间上至少有一个实数根,所以或,解不等式即可得解
【详解】
由题意得,在区间上至少有一个实数根,
而的根为,区间的长度为2,
故区间内必含有2或.
∴或,
∴或,
故选:B.
34.D
【分析】
构造,由题设条件判断、上的单调性,根据等价于,结合单调性即可求的范围.
【详解】
令,当时,,
∴,单调递减,
∵分别是定义在上的偶函数和奇函数,
∴,故在上是奇函数,
∴时,单调递减,
由题设知:要使成立,即成立,
当时,有;当时,有;
∴.
故选:D
35.AC
【分析】
利用导数可判断AC的正误,求出函数的零点可判断B的正误,利用反例可判断D的正误.
【详解】
,其中,
令,则,
当时,;当时,,
故在上为减函数,在上为增函数,
故时,,时,,
故时,,
所以在,上均为增函数,故A正确,
设,,
令,则,
当时,,故在,上均为增函数,
故当时,;当时,,
故当时,;当时,,
故在,上均为增函数,故C正确.
令,故(舍),故B错误.
,故,故不是奇函数,故D错误.
故选:AC.
36.AD
【分析】
构造函数,利用导数分析函数在上的单调性,由此可判断各选项的正误.
【详解】
因为,所以,,
又,所以.
构造函数,,
则,所以在上为增函数,
因为,所以,
所以,即,故A正确;
因为,所以,
所以,即,故B错误;
因为,所以,
所以,即,故C错误;
因为,所以,
所以,即,故D正确,
故选:AD.
37.ACD
【分析】
构造函数利用导数判断函数的单调性即可判断A;构造函数,利用导数求出函数的单调性,即可判断B;构造函数利用导数说明其单调性,即可判断C,构造函数利用导数研究函数的单调性,即可判断D;
【详解】
解:对于A:令,则,
故在递增,因为,所以,即,故A正确;
对于B:令,则,因为当时,所以,即在上单调递减,所以,即,即,故B错误;
对于C:令,,当时,,即在上单调递增,又,所以,即,所以,故C正确;
对于D:令,则,所以在定义域上单调递增,又,所以,所以当时,即,所以,故的解集为,故D正确;
故选:ACD
38.AB
【分析】
首先根据条件构造函数,由导数判断函数的单调性,不等式转化为,利用单调性,即可求解的值.
【详解】
解析:设,则.
,
,
,即函数在定义域上单调递减.
,
,
不等式等价于,即,解得.故不等式的解集为.
故选:.
39.AB
【分析】
构造函数,判断出是偶函数,故关于的方程有4个不同的实数根等价于在上有两个零点.
当时,等价于,
令,利用导数研究函数的单调性,极值,得到,对照四个选项进行验证即可.
【详解】
构造函数, 的定义域为,且,即是偶函数,故关于的方程有4个不同的实数根等价于在上有两个零点.
当时,,则等价于,令,则.令,则,故在区间上单调递增.又,所以在区间上单调递减,在区间上单调递增,即在处取得极小值且.当时,;当时,,故当时,关于的方程在区间上有两个不同的实数根,即关于的方程有个不同的实数根.
对照四个选项:A、B符合,故选:A B.
【点睛】
已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
40.,
【分析】
由题意得到恒成立,利用分离参数法和基本不等式即可求出的取值范围.
【详解】
解:在上是增函数,
,
,
由基本不等式得:(当且仅当,即时取“”,
,
,解得,
故答案为:,,
41.##
【分析】
不等式的解集即为函数的单调减区间,根据根据函数的图像求出单调减区间,即可得出答案.
【详解】
解:根据函数图像可知,函数在和上递减,
所以不等式≤0的解集为.
故答案为:.
42.
【分析】
求导可得在上单调递增,结合是奇函数,可转化
为,借助单调性和定义域,列出不等式组,即得解
【详解】
因为时,,所以在上单调递增.
又是奇函数,由,
得,
所以,解得,
所以实数的取值范围为.
故答案为:
43.②③④
【分析】
对求导,由导函数的符号可判断的单调性,即可判断①;
由,以及的单调性即可判断②;
令,由零点存在定理可判断③;
等价于,有一个根为,所以原方程有4个根等价于方程有个实数解,令,对求导判断单调性,作出函数图象,数形结合即可判断④.
【详解】
由可得,
由可得:,由可得:,
所以在单调递减,在单调递增,故①不正确;
对于选项②:,根据在单调递增,
所以,故②正确;
对于选项③:令,因为,
,,根据零点存在定理可知存在使得,所以方程有实数解,故③正确;
对于选项④:方程即,有一根为,所以原方程有4个根等价于方程有个实数解,
令,则,
令可得或,
令可得,
所以在和单调递增,在单调递减,
,
作出,的图形如图所示:
所以存在时,方程有个实数解,此时方程有4个实数解,故④正确.
故答案为:②③④
【点睛】
方法点睛:利用导数研究函数单调性的方法:
(1)确定函数的定义域;求导函数,由(或)解出相应的的范围,对应的区间为的增区间(或减区间);
(2)确定函数的定义域;求导函数,解方程,利用的根将函数的定义域分为若干个子区间,在这些子区间上讨论的正负,由符号确定在子区间上的单调性.
44.(1)增区间是(-∞,-3),(2,+∞);减区间是(-3,2) ;(2)单调递减区间为(0,π) .
【分析】
求出导函数,由得增区间,由得减区间.
【详解】
解:(1)=6x2+6x-36.
由>0得6x2+6x-36>0,解得x<-3或x>2;
由<0解得 -3故f(x)的增区间是(-∞,-3),(2,+∞);
减区间是(-3,2).
(2)=cos x-1.
因为0故函数f(x)的单调递减区间为(0,π),无增区间.
45.(1)单调递增区间为,,单调递减区间为;(2).
【分析】
(1)利用求得的单调区间;
(2)由在区间恒成立分离常数,结合二次函数的性质求得的取值范围.
【详解】
(1)当a=﹣3时,函数f(x)=x﹣﹣4lnx(x>0),
=1+﹣==,
由>0,可得0<x<1或x>3,
由<0,可得1<x<3,
所以f(x)的单调递增区间为(0,1),(3,+∞);递减区间为(1,3);
(2)=1﹣﹣=,x>0,
f(x)在区间(0,+∞)上单调递增,
即为≥0在区间(0,+∞)上恒成立,
即a≤x2﹣4x=(x﹣2)2﹣4在区间(0,+∞)上恒成立,
由(x2﹣4x)min=﹣4,得a≤﹣4,
即a∈.
46.(1)答案不唯一,具体见解析;(2).
【分析】
(1)求出导函数,讨论、或,利用导数与函数单调性之间的关系即可求解.
(2)根据题意若存在,,使得不等式成立,只需使,求出,由(1)可知函数的单调性,根据单调性讨论函数的最小值即可.
【详解】
解:(1)根据题意,,
,,或,
所以①当时,,则有,或;,
此时可得,在,上单调递增,在上单调递减.
②当时,,则有,或;,
此时可得,在,,上单调递增,在上单调递减.
③当时,恒有,此时函数在上单调递增.
综上可得,①当时,在,上单调递增,在上单调递减.
②当时,在,,上单调递增,在上单调递减.
③当时,函数在上单调递增.
(2)根据题意,由(1)可得,,
若存在,,使得不等式成立,则需使,
,
由(1)可知,①当时,,则有,或;,
此时可得,在,上单调递增,在上单调递减,
即得在,上单调递增,故有;
②当时,,则有,或;,
此时可得,在,,上单调递增,在上单调递减.
当时,即时,在,上单调递减,
则有,不合题意;
当时,即时,在,上单调递减,在,
则有,
此时令,则,
即得此时在上单调递增,
所以(1)恒成立,即恒成立,不合题意;
综上可得,.
47.
(1)
(2)
【分析】
(1)由在上单调递减,得到恒成立,用分离参数法求出实数a的取值范围;
(2)由在上存在单调递减区间,得到有解,用分离参数法求出实数a的取值范围.
(1)
因为在上单调递减,所以当时,恒成立,即恒成立,令,则,而.
因为,所以.所以(此时),所以.
当时,.
因为,所以,即在上为减函数,又,所以实数a的取值范围是.
(2)
因为,,所以.
因为在上存在单调递减区间,所以当时,有解,即有解.
设,所以只要即可,而,所以,所以.
又,所以或.所以实数a的取值范围为.
48.(1)在上单调递增,在,上单调递减;(2).
【分析】
(1)依题意,即可求出参数的值,从而得到函数解析式,再求出函数的导函数,从而得到函数的单调区间;
(2)由(1)可得函数的极值,从而得到函数图象,有个不同实数根等价于与有个不同的交点,数形结合即可求出参数的取值范围;
【详解】
解:(1),,.
,
当和时,;当时,;
在上单调递增,在,上单调递减,
(2)由(1)可知,的极大值为,极小值为,且当时,,当时,,由此可得大致图象如图:
有个不同实数根等价于与有个不同的交点,
由图象可知:,解得,的取值范围为.
试卷第1页,共3页
5.3 导数在研究函数中的应用
5.3.1 函数的单调性
【题型归纳】
题型一:利用导数求函数的单调性(不含参)
1.(2021·广西河池·高二月考(理))函数在上的单调减区间为( )
A. B. C. D.
2.(2021·全国·高二单元测试)已知函数f(x)与其导函数f'(x)的图象如图所示,则函数g(x)=的单调递减区间为( )
A.(0,1)和(4,+∞) B.(0,2)
C.(﹣∞,0)和(1,4) D.(0,3)
3.(2021·陕西·绥德中学高二月考(理))若曲线在点处的切线过点,则函数的单调递减区间为( )
A. B.
C. D.,
题型二:由函数的单调性求参数
4.(2021·广东·东莞市光明中学高二月考)若在上是减函数,则的取值范围是( )
A. B.
C. D.
5.(2021·陕西·渭南市尚德中学高二月考(理))已知在R上是增加的,则的取值范围是( )
A. B. C.或 D.或
6.(2021·山东·兰陵四中高二期中)若函数在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
题型三:由函数在区间的单调性求参数
7.(2021·重庆市清华中学校高二月考)若函数在区间内存在单调递增区间,则实数的取值范围是( )
A. B. C. D.
8.(2021·全国·高二课时练习)已知函数在上为减函数,则实数a的取值范围是( )
A. B. C. D.
9.(2021·河南·高二期末(理))若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
题型四:函数与导函数图像的关系
10.(2021·广西河池·高二月考(理))如果函数的导函数的图象如图所示,则以下关于函数的判断:
①在区间内单调递增;②在区间内单调递减;③在区间内单调递增;
④是极小值点;⑤是极大值点.
其中不正确的是( )
A.③⑤ B.②③ C.①④⑤ D.①②④
11.(2021·重庆第二外国语学校高二月考)已知函数的图象如图所示,则函数的图象可能是图中的( )
A.B.C. D.
12.(2021·江苏·高二课时练习)已知函数的图像如图所示,是的导函数,则下列结论正确的是( )
A. B.
C. D.
题型五:含参分类讨论函数的单调性
13.(2021·全国·高二课时练习)已知函数,.讨论函数的单调区间.
14.(2021·全国·高二课时练习)已知函数.
(1)讨论函数的单调性;
(2)当时,恒成立,求整数k的最大值.
15.(2021·全国·高二课时练习)设函数f(x)=aln x+,其中a为常数.
(1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
【双基达标】
一、单选题
16.(2021·全国·高二课时练习)函数在上的单调性是( ).
A.单调递增
B.单调递减
C.在上单调递减,在上单调递增
D.在上单调递增,在上单调递减
17.(2021·全国·高二课时练习)已知函数的导函数有下列信息:
①时,;
②时,或;
③时,或.
则函数的大致图像是图中的( ).
A. B.
C. D.
18.(2021·广西河池·高二月考(理))定义在上的函数其导函数恒成立,且,则不等式的解集为( )
A. B. C. D.
19.(2021·河北承德第一中学高二月考)在上可导的函数的图象如图所示,则关于的不等式的解集为( )
A. B.
C. D.
20.(2021·全国·高二单元测试)定义域为R的函数且,且的导函数,则实数a的取值范围为( )
A. B. C. D.
21.(2021·全国·高二单元测试)已知函数,则在上不单调的一个充分不必要条件是( )
A. B.
C. D.
22.(2021·江苏·高二课时练习)已知函数的导函数为,对任意的实数都有,,则不等式的解集是( )
A. B. C. D.
23.(2021·新疆维吾尔自治区喀什第二中学高二期中)设f'(x)是函数f(x)的导函数,若f'(x)>0,且 x1,x2∈R(x1≠x2),f(x1)+f(x2)<2f(),则下列各项中不一定正确的是( )
A.f(2)<f(e)<f(π)
B.f′(π)<f′(e)<f′(2)
C.f(2)<f′(2)﹣f′(3)<f(3)
D.f′(3)<f(3)﹣f(2)<f′(2)
24.(2021·全国·高二专题练习)设函数是偶函数的导数, ,当时, ,则使|f(x)|>成立的x的取值范围是( )
A. B.
C. D.
25.(2021·全国·高二专题练习)定义在R上的偶函数,其导函数,当x≥0时,恒有,若,则不等式的解集为( )
A.(,1) B.(∞,)∪(1,+∞)
C.(,+∞) D.(∞,)
【高分突破】
一:单选题
26.(2021·江苏·南京市中华中学高二期中)已知函数在区间,上是单调增函数,则实数的取值范围为( )
A. B. C. D.
27.(2021·江西·景德镇一中高二期中)函数的图象大致是( )
A. B.
C. D.
28.(2021·全国·高二单元测试)设为实数,函数,且是偶函数,则的单调递增区间为( )
A. B.,
C. D.
29.(2021·广西·蒙山中学高二月考(理))已知定义在R上的函数f(x)满足f(2)=20,且f(x)的导函数满足,则不等式f(x)>2x3+2x的解集为( )
A.{x|x>-2} B.{x|x>2} C.{x|x<2} D.{x|x<-2或x>2}
30.(2021·江苏·高二课时练习)已知函数及其导函数满足且.若恒成立,则( )
A. B.
C. D.
31.(2021·北京一七一中高二月考)已知函数,且,则下列叙述正确的是( )
A. B.
C. D.
32.(2021·全国·高二课时练习)已知定义在上的函数满足对,其中是函数的导函数,若,则实数的取值范围为( )
A. B.
C. D.
33.(2021·全国·高二课时练习)若函数在区间上不是单调函数,则实数的取值范围是( )
A. B.
C. D.不存在这样的实数
34.(2021·浙江·临海市西湖双语实验学校高二月考)设分别是定义在上的偶函数和奇函数,为其导函数.当时,且.则使得不等式成立的的取值范围是( )
A. B.
C. D.
二、多选题
35.(2021·重庆十八中高二月考)已知函数,则( )
A.在定义域内单调性不变 B.在定义域内有零点
C.的导数在定义域内单调性不变 D.为奇函数
36.(2021·全国·高二单元测试)已知函数,,是其导函数,恒有,则( )
A. B.
C. D.
37.(2021·江苏省苏州第十中学校高二月考)已知是定义在R上函数,是的导数,则以下说法正确的是( )
A.若,则;
B.当时,可,则;
C.当时,可,且,则;
D.若,且,则的解集为
38.(2021·广东茂名·高二期末)已知函数是定义在上的可导函数,其导函数为,若,且,则使不等式成立的的值不可能为( )
A. B. C. D.
39.(2020·广东·广州市协和中学高二期中)已知函数,若关于的方程有4个不同的实数根,则实数的取值可以为( )
A. B. C. D.
三、填空题
40.(2021·浙江杭州·高二期中)已知函数在上是增函数,则实数的取值范围是__.
41.(2021·全国·高二课时练习)函数y=f(x)在其定义域内可导,其图象如图所示,记y=f(x)的导函数为y=,则不等式≤0的解集为________.
42.(2021·全国·高二单元测试)已知奇函数的导函数为,,若,则实数的取值范围为______.
43.(2021·江西上饶·高二月考(理))已知函数,则以下结论正确的是___________.
①在R上单调递增
②
③方程有实数解
④存在实数k,使得方程有4个实数解
四、解答题
44.(2021·全国·高二课时练习)求下列函数的单调区间:
(1)f(x)=2x3+3x2-36x+1;
(2)f(x)=sin x-x(0
(1)当时,求的单调区间;
(2)若在区间上单调递增,求的取值范围.
46.(2021·江苏·无锡市第一中学高二期中)已知函数,其中为正实数.
(1)试讨论函数的单调性;
(2)设,若存在,,使得不等式成立,求的取值范围.
47.(2021·全国·高二课时练习)已知函数,,.
(1)若函数在上单调递减,求实数a的取值范围;
(2)若函数存在单调递减区间,求实数a的取值范围.
48.(2021·河南·辉县市第一高级中学高二月考(理))已知函数的图象过点,若关于的方程有3个不同的实数根,
(1)求函数的单调区间;
(2)求的取值范围.
【答案详解】
1.C
【分析】
求导,令导函数小于零,解不等式即可
【详解】
解:由已知
令,且
则,
即单调减区间为
故选:C.
2.A
【分析】
结合函数图象,求出f′(x)﹣f(x)<0成立的x的范围即可.
【详解】
根据导函数和函数的关系可判断两函数如图:
结合图象:x∈(0,1)和x∈(4,+∞)时,f′(x)﹣f(x)<0,
所以,
故g(x)在(0,1),(4,+∞)递减,
故选:A
3.D
【分析】
先利用导数求出函数在处的切线方程,然后将点代入切线方程,即可求出的值,最后利用导数的符号大于零即可求解.
【详解】
由题意得,
所以,且.
故函数在,处的切线为:
,将点代入得.
则,由得且.
故的单调递减区间为,.
故选:D.
4.C
【分析】
先求,再将在上是减函数,转化为在上恒成立,而后分离参数求在上的最小值,可得实数的取值范围.
【详解】
由题知,,.
若在上是减函数,则在上恒成立,
由得,,
当时,,
所以.
故选:C.
5.B
【分析】
由题意得函数的导数大于等于0,可得在上恒成立,利用一元二次函数的图象,即可得到答案;
【详解】
由题意得函数的导数大于等于0,可得在上恒成立,
,
故选:B
6.D
【分析】
首先利用导数求函数的减区间,再利用子集关系,列式求的取值范围.
【详解】
,
当,解得:,
由条件可知,
所以 ,解得:.
故选:D
7.D
【分析】
求出函数的导数,问题转化为 而 在 递增,求出 的最小值,从而求出的范围即可 .
【详解】
若在区间内存在单调递增区间,则有解,
故
令
在递增 ,
故
故选:D
8.B
【分析】
求出导函数,将问题转化为在上恒成立,进而得出,分析不具有单调性,从而可得.
【详解】
由题意,得,又在上恒成立,所以.
而当时,恒为0,此时(),不具有单调性,
所以,即实数a的取值范围为.
故选:B
9.B
【分析】
根据函数的区间单调性,应用导数可得在上恒成立,构造并研究单调性即可求的取值范围.
【详解】
由,得,
由在上单调递减,得在上恒成立,即在上恒成立.
令,在上,
∴在上单调递减,即,
∴,故的取值范围.
故选:.
10.A
【分析】
根据导函数与单调性和极值点的关系,观察图像即可得出答案.
【详解】
由图可知,
在区间内,有正有负,①错误;
在区间内,,在区间内单调递增,②错误;
在区间内,,在区间内单调递增,③正确;
不存在,使当时,,当时,,④错误;
存在,使当时,,当时,,如,⑤正确
故选:A.
11.C
【分析】
由函数的图象的增减变化趋势,判断函数取值的正、负,由此判断可得选项.
【详解】
解:由函数的图象的增减变化趋势,判断函数取值的正、负情况如下表:
x
递减 递增 递减
所以当时,函数的图象在x轴下方;
当时,函数的图象在x轴上方;
当时,函数的图象在x轴下方.
故选:C.
12.B
【分析】
结合图象,判断出的大小关系.
【详解】
由题图可知函数的图像在处的切线的斜率比在处的切线的斜率大,且均为正数,所以.
的斜率为,其比在处的切线的斜率小,但比在处的切线的斜率大,所以.
故选:B
13.答案见解析
【分析】
求导可得,对和的大小进行分类讨论可得函数的单调区间.
【详解】
函数定义域是,
,
①当时,即时,当或时,;当时,.
此时,的增区间是和,减区间是,
②当时,对任意的恒成立,
此时,函数增区间,无减区间;
③当时,即时,当或时,;当时,.
此时,函数的增区间是和,减区间是.
综上,当时,函数的增区间是和,减区间是;
当时,函数的增区间是;
当时,函数的增区间是和,减区间是;
14.
(1)答案见解析;
(2)1.
【分析】
(1)求出函数导数后,分三种情况讨论,即可求解函数单调区间;
(2)分离参数可得对于恒成立,令,利用导数求出函数,分析出,即可求出整数k的最大值.
(1)
由得.
当时,,故在上单调递增;
当时,令,解得.
故在上单调递减,在上单调递增;
当时,,故在上单调递减.
(2)
原不等式等价于对于恒成立.
令,则.
令,则,所以在上单调递增.
又,,
所以存在,使得,
且在上单调递减,在上单调递增,
所以,
又,所以,
所以,所以,
经验证时,恒成立,所以整数k的最大值为1.
15.(1)x-2y-1=0;(2)答案见解析.
【分析】
(1)先求出的值,得出切点坐标,再求出的值,得到切线的斜率,从而得到切线方程.
(2)先求出,对二次函数的开口方向,判别式进行分类讨论即可.
【详解】
(1)由题意知a=0时,,x∈(0,+∞).
此时f′(x)=.可得f′(1)=,又f(1)=0,
所以曲线y=f(x)在(1,f(1))处的切线方程为x-2y-1=0.
(2)函数f(x)的定义域为(0,+∞),f′(x)=+=.
当a≥0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增.
当a<0时,令g(x)=ax2+(2a+2)x+a,由于=(2a+2)2-4a2=4(2a+1),
①当时,,
f′(x)=≤0,函数f(x)在(0,+∞)上单调递减.
②当时,<0,g(x)<0,f′(x)<0,函数f(x)在(0,+∞)上单调递减.
③当-时,>0.
设x1,x2(x1
由x1==,
所以x∈(0,x1)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
x∈(x1,x2)时,g(x)>0,f′(x)>0,函数f(x)单调递增,
x∈(x2,+∞)时,g(x)<0,f′(x)<0,函数f(x)单调递减,
综上可得:当a≥0时,函数f(x)在(0,+∞)上单调递增;
当时,函数f(x)在(0,+∞)上单调递减;
当时,函数f(x)在,上单调递减,在上单调递增.
16.C
【分析】
利用导数判断函数在上的单调性.
【详解】
,令,得;
令,得,
∴函数在上单调递减,在上单调递增.
故选:C
17.C
【分析】
根据导数的正负与函数的单调性关系判断.
【详解】
根据导函数信息知,函数在上是增函数,在,上是减函数.
故选:C.
18.C
【分析】
根据题意,设g(x)=f(x) 3x,求出其导数,分析可得g′(x)<0,则g(x)在R上为减函数,又由f(1)=3,则g(1)=0, ,结合函数的单调性分析可得答案.
【详解】
解:设g(x)=f(x) 3x,则g′(x)=f′(x) 3,
又由f′(x)<3,则g′(x)<0,则g(x)在R上为减函数,
又由f(1)=3,则g(1)=f(1) 3=0,
则g(x)过点,且在R上为减函数,
由得
即,由于过点,且在R上为增函数,
则必有
故选:C
19.A
【分析】
根据单调性导数的关系得出和的解集,然后可得题设不等式的解集.
【详解】
由题意的解集为,,的解集为,
或,所以或.
故选:A.
20.B
【分析】
由题可得函数为R上的单调递增函数,即求.
【详解】
由可知,设,
,是R上的单调递增函数.
由且,可知且,
.
故选:B.
21.D
【分析】
求出函数的导数,问题转化为函数与x轴在上有交点,即求.
【详解】
函数的定义域为,,
令,
若在上不单调,则函数与x轴在上有交点,
又,
则,
解得,
故在上不单调的一个充分不必要条件是.
故选:D.
22.C
【分析】
由已知条件构造函数,再根据,求,不等式转化为,结合函数的单调性和奇偶性,解抽象不等式.
【详解】
解:由题意得,
则
,
由,解得:,
故,
(2),
当时,,,,
在上恒成立,
即在上单调递增,
又,故为上的偶函数,
其图象关于轴对称,在上单调递减,
故,故,
故选:C.
23.C
【分析】
f′(x)>0,∴f(x)在R上单调递增,由,可得<,可得y=f(x)的图象如图所示,图象是向上凸.进而判断出正误.
【详解】
解:∵f′(x)>0,∴f(x)在R上单调递增,
∵,
∴<,
∴y=f(x)的图象如图所示,图象是向上凸.
∴f(2)<f(e)<f(π),f′(π)<f′(e)<f′(2),可知:A,B正确.
∵f(3)﹣f(2)=,表示点A(2,f(2)),B(3,f(3))的连线的斜率.
由图可知:f′(3)<kAB<f′(2),故D正确.
C项无法推出,
故选:C.
24.C
【分析】
设,根据函数的单调性和奇偶性问题转化为,求出不等式的解集即可.
【详解】
解:设F(x)=xf(x),
易知函数F(x)为奇函数,且当x<0时,F′(x)=xf′(x)+f(x)>0,
故函数F(x)在R递增,
将目标不等式转化为|F(x)|>F(1)=1,
结合函数的单调性得:|x|>1,解得:或x>1,
故不等式的解集是(﹣∞,﹣1)∪(1,+∞),
故选:C.
25.A
【分析】
由已知可得,即在上单调递减,再利用函数的奇偶性、单调性,求解题设不等式即可.
【详解】
当时,,又,
∴,即在上单调递减.
∵是定义在R上的偶函数,
∴是定义在R上的偶函数,
由不等式,则有,
∴,解得:.
∴不等式的解集为.
故选:A
26.D
【分析】
由题意得到在,恒成立,利用分离参数法和基本不等式即可求出实数的取值范围.
【详解】
解:在区间,上是单调增函数,
当,时,恒成立,
,
又(当且仅当时取等号),即,
.
故选:D.
27.A
【分析】
由函数有两个零点排除选项C,D;再借助导数探讨函数的单调性与极值情况即可判断作答.
【详解】
由得,或,选项C,D不满足;
由求导得,当或时,,当时,,
于是得在和上都单调递增,在上单调递减,在处取极大值,在处取极小值,B不满足,A满足.
故选:A
28.B
【分析】
先利用定义算出,在求导算出单调区间.
【详解】
因为,所以,
因为是偶函数,所以对恒成立,
即,即,
所以,所以,令,解得或,
所以的单调递增区间为,.
故选:B.
29.B
【分析】
根据给定条件构造函数并判断其单调性,再利用的单调性即可求出不等式f(x)>2x3+2x的解集.
【详解】
令,因,则,即在R上单调递增,
因,则不等式f(x)>2x3+2x等价于,于是得x>2,
所以原不等式的解集为{x|x>2}.
故选:B
30.D
【分析】
构造函数,通过题意,可得函数的单调区间,以及,
从而可得,再通过分离参数,即可求解.
【详解】
解:设,则,
当时,,当时,
在上单调递增,在上单调递减,
,
不等式可转化为,
该不等式恒成立,
则,
故选:D.
31.B
【分析】
根据题意,求出函数的导数,分析可得区间上为增函数,据此分析可得答案.
【详解】
根据题意,函数,其导数,
在区间上,,函数为增函数,
若,则,
故选:B.
32.D
【分析】
引入新函数,求导后确定的单调性,由单调性解不等式.
【详解】
令,,则,
因为,所以,所以函数在上单调递减.
因为,所以,所以,
即,所以且,解得,
所以实数的取值范围为.
故选:D.
【点睛】
易错点睛:应用导数研究函数的单调性、极值、最值等性质时,首先要考虑函数的定义域,即单调区间、极值点都要在函数的定义域内,本题容易因忽略而出错.
33.B
【分析】
根据题意,导函数在区间上有正有负,所以在区间上至少有一个实数根,所以或,解不等式即可得解
【详解】
由题意得,在区间上至少有一个实数根,
而的根为,区间的长度为2,
故区间内必含有2或.
∴或,
∴或,
故选:B.
34.D
【分析】
构造,由题设条件判断、上的单调性,根据等价于,结合单调性即可求的范围.
【详解】
令,当时,,
∴,单调递减,
∵分别是定义在上的偶函数和奇函数,
∴,故在上是奇函数,
∴时,单调递减,
由题设知:要使成立,即成立,
当时,有;当时,有;
∴.
故选:D
35.AC
【分析】
利用导数可判断AC的正误,求出函数的零点可判断B的正误,利用反例可判断D的正误.
【详解】
,其中,
令,则,
当时,;当时,,
故在上为减函数,在上为增函数,
故时,,时,,
故时,,
所以在,上均为增函数,故A正确,
设,,
令,则,
当时,,故在,上均为增函数,
故当时,;当时,,
故当时,;当时,,
故在,上均为增函数,故C正确.
令,故(舍),故B错误.
,故,故不是奇函数,故D错误.
故选:AC.
36.AD
【分析】
构造函数,利用导数分析函数在上的单调性,由此可判断各选项的正误.
【详解】
因为,所以,,
又,所以.
构造函数,,
则,所以在上为增函数,
因为,所以,
所以,即,故A正确;
因为,所以,
所以,即,故B错误;
因为,所以,
所以,即,故C错误;
因为,所以,
所以,即,故D正确,
故选:AD.
37.ACD
【分析】
构造函数利用导数判断函数的单调性即可判断A;构造函数,利用导数求出函数的单调性,即可判断B;构造函数利用导数说明其单调性,即可判断C,构造函数利用导数研究函数的单调性,即可判断D;
【详解】
解:对于A:令,则,
故在递增,因为,所以,即,故A正确;
对于B:令,则,因为当时,所以,即在上单调递减,所以,即,即,故B错误;
对于C:令,,当时,,即在上单调递增,又,所以,即,所以,故C正确;
对于D:令,则,所以在定义域上单调递增,又,所以,所以当时,即,所以,故的解集为,故D正确;
故选:ACD
38.AB
【分析】
首先根据条件构造函数,由导数判断函数的单调性,不等式转化为,利用单调性,即可求解的值.
【详解】
解析:设,则.
,
,
,即函数在定义域上单调递减.
,
,
不等式等价于,即,解得.故不等式的解集为.
故选:.
39.AB
【分析】
构造函数,判断出是偶函数,故关于的方程有4个不同的实数根等价于在上有两个零点.
当时,等价于,
令,利用导数研究函数的单调性,极值,得到,对照四个选项进行验证即可.
【详解】
构造函数, 的定义域为,且,即是偶函数,故关于的方程有4个不同的实数根等价于在上有两个零点.
当时,,则等价于,令,则.令,则,故在区间上单调递增.又,所以在区间上单调递减,在区间上单调递增,即在处取得极小值且.当时,;当时,,故当时,关于的方程在区间上有两个不同的实数根,即关于的方程有个不同的实数根.
对照四个选项:A、B符合,故选:A B.
【点睛】
已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
40.,
【分析】
由题意得到恒成立,利用分离参数法和基本不等式即可求出的取值范围.
【详解】
解:在上是增函数,
,
,
由基本不等式得:(当且仅当,即时取“”,
,
,解得,
故答案为:,,
41.##
【分析】
不等式的解集即为函数的单调减区间,根据根据函数的图像求出单调减区间,即可得出答案.
【详解】
解:根据函数图像可知,函数在和上递减,
所以不等式≤0的解集为.
故答案为:.
42.
【分析】
求导可得在上单调递增,结合是奇函数,可转化
为,借助单调性和定义域,列出不等式组,即得解
【详解】
因为时,,所以在上单调递增.
又是奇函数,由,
得,
所以,解得,
所以实数的取值范围为.
故答案为:
43.②③④
【分析】
对求导,由导函数的符号可判断的单调性,即可判断①;
由,以及的单调性即可判断②;
令,由零点存在定理可判断③;
等价于,有一个根为,所以原方程有4个根等价于方程有个实数解,令,对求导判断单调性,作出函数图象,数形结合即可判断④.
【详解】
由可得,
由可得:,由可得:,
所以在单调递减,在单调递增,故①不正确;
对于选项②:,根据在单调递增,
所以,故②正确;
对于选项③:令,因为,
,,根据零点存在定理可知存在使得,所以方程有实数解,故③正确;
对于选项④:方程即,有一根为,所以原方程有4个根等价于方程有个实数解,
令,则,
令可得或,
令可得,
所以在和单调递增,在单调递减,
,
作出,的图形如图所示:
所以存在时,方程有个实数解,此时方程有4个实数解,故④正确.
故答案为:②③④
【点睛】
方法点睛:利用导数研究函数单调性的方法:
(1)确定函数的定义域;求导函数,由(或)解出相应的的范围,对应的区间为的增区间(或减区间);
(2)确定函数的定义域;求导函数,解方程,利用的根将函数的定义域分为若干个子区间,在这些子区间上讨论的正负,由符号确定在子区间上的单调性.
44.(1)增区间是(-∞,-3),(2,+∞);减区间是(-3,2) ;(2)单调递减区间为(0,π) .
【分析】
求出导函数,由得增区间,由得减区间.
【详解】
解:(1)=6x2+6x-36.
由>0得6x2+6x-36>0,解得x<-3或x>2;
由<0解得 -3
减区间是(-3,2).
(2)=cos x-1.
因为0
45.(1)单调递增区间为,,单调递减区间为;(2).
【分析】
(1)利用求得的单调区间;
(2)由在区间恒成立分离常数,结合二次函数的性质求得的取值范围.
【详解】
(1)当a=﹣3时,函数f(x)=x﹣﹣4lnx(x>0),
=1+﹣==,
由>0,可得0<x<1或x>3,
由<0,可得1<x<3,
所以f(x)的单调递增区间为(0,1),(3,+∞);递减区间为(1,3);
(2)=1﹣﹣=,x>0,
f(x)在区间(0,+∞)上单调递增,
即为≥0在区间(0,+∞)上恒成立,
即a≤x2﹣4x=(x﹣2)2﹣4在区间(0,+∞)上恒成立,
由(x2﹣4x)min=﹣4,得a≤﹣4,
即a∈.
46.(1)答案不唯一,具体见解析;(2).
【分析】
(1)求出导函数,讨论、或,利用导数与函数单调性之间的关系即可求解.
(2)根据题意若存在,,使得不等式成立,只需使,求出,由(1)可知函数的单调性,根据单调性讨论函数的最小值即可.
【详解】
解:(1)根据题意,,
,,或,
所以①当时,,则有,或;,
此时可得,在,上单调递增,在上单调递减.
②当时,,则有,或;,
此时可得,在,,上单调递增,在上单调递减.
③当时,恒有,此时函数在上单调递增.
综上可得,①当时,在,上单调递增,在上单调递减.
②当时,在,,上单调递增,在上单调递减.
③当时,函数在上单调递增.
(2)根据题意,由(1)可得,,
若存在,,使得不等式成立,则需使,
,
由(1)可知,①当时,,则有,或;,
此时可得,在,上单调递增,在上单调递减,
即得在,上单调递增,故有;
②当时,,则有,或;,
此时可得,在,,上单调递增,在上单调递减.
当时,即时,在,上单调递减,
则有,不合题意;
当时,即时,在,上单调递减,在,
则有,
此时令,则,
即得此时在上单调递增,
所以(1)恒成立,即恒成立,不合题意;
综上可得,.
47.
(1)
(2)
【分析】
(1)由在上单调递减,得到恒成立,用分离参数法求出实数a的取值范围;
(2)由在上存在单调递减区间,得到有解,用分离参数法求出实数a的取值范围.
(1)
因为在上单调递减,所以当时,恒成立,即恒成立,令,则,而.
因为,所以.所以(此时),所以.
当时,.
因为,所以,即在上为减函数,又,所以实数a的取值范围是.
(2)
因为,,所以.
因为在上存在单调递减区间,所以当时,有解,即有解.
设,所以只要即可,而,所以,所以.
又,所以或.所以实数a的取值范围为.
48.(1)在上单调递增,在,上单调递减;(2).
【分析】
(1)依题意,即可求出参数的值,从而得到函数解析式,再求出函数的导函数,从而得到函数的单调区间;
(2)由(1)可得函数的极值,从而得到函数图象,有个不同实数根等价于与有个不同的交点,数形结合即可求出参数的取值范围;
【详解】
解:(1),,.
,
当和时,;当时,;
在上单调递增,在,上单调递减,
(2)由(1)可知,的极大值为,极小值为,且当时,,当时,,由此可得大致图象如图:
有个不同实数根等价于与有个不同的交点,
由图象可知:,解得,的取值范围为.
试卷第1页,共3页
