鲁教版(五四学制)七年级数学上册 1.3 探索三角形全等的条件学案 (共3课时)(无答案)
文档属性
| 名称 | 鲁教版(五四学制)七年级数学上册 1.3 探索三角形全等的条件学案 (共3课时)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 08:52:24 | ||
图片预览


文档简介
3 探索三角形全等的条件(1)
【学习目标】
1.经历探索三角形全等的“边边边”的条件的过程.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
【自主学习】
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
1.作图方法:
先画一线段AB,使得AB=6cm,再分别以A、B为圆心,8cm、10cm为半径画弧,两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=6cm,AC=8cm,BC=10cm.
2.以小组为单位,把剪下的三角形重叠在一起,发现都能够重合.这说明这些三角形都是全等的.
这反映了一个规律:
_______________的两个三角形全等,简写为_________或_________.
用三根木条钉成三角形框架,它的大小和形状是固定不变的,而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的__________.
【合作探究】
如图,1、如图,△ABC中 AB=AC, D为BC中点
求证:①△ABD≌△ACD.
②∠BAD=∠CAD
③AD⊥BC
证明:
【精讲点拨】
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么?
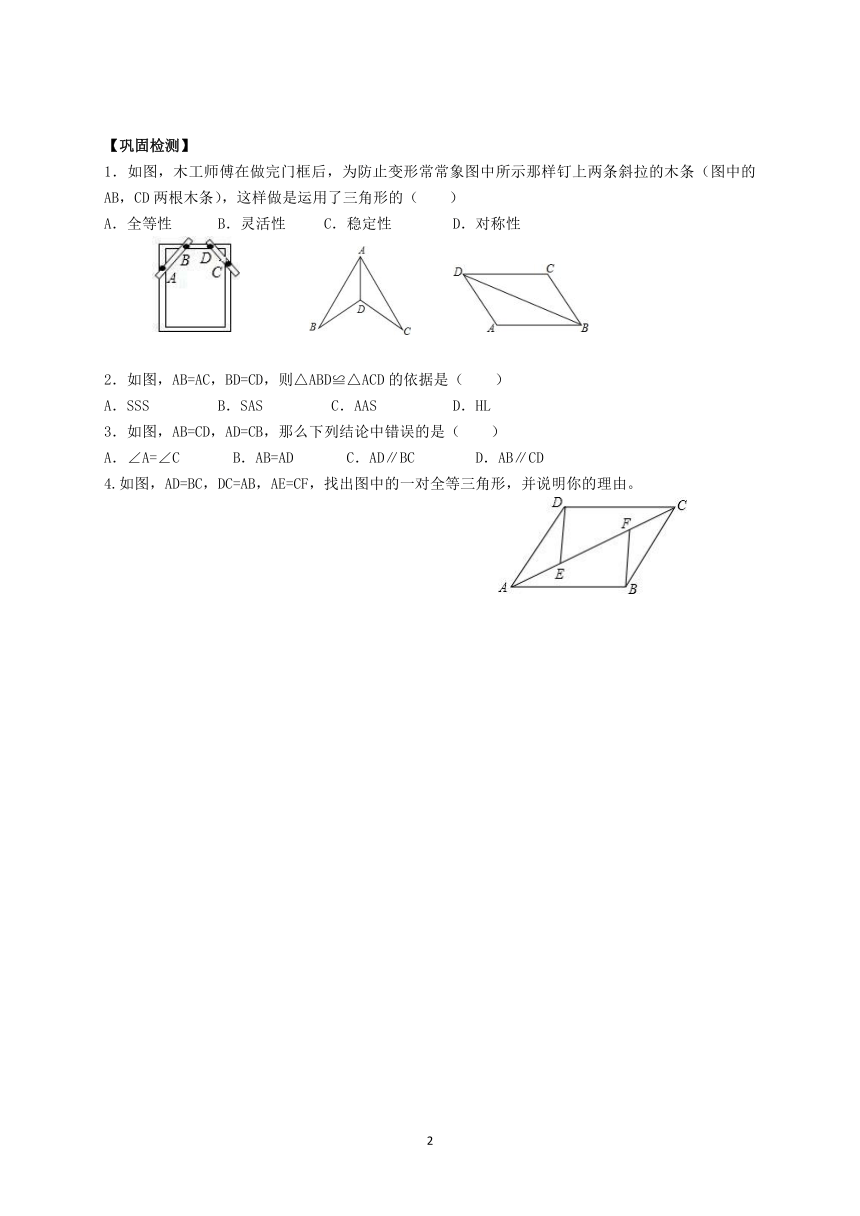
【巩固检测】
1.如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的AB,CD两根木条),这样做是运用了三角形的( )
A.全等性 B.灵活性 C.稳定性 D.对称性
2.如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD
4.如图,AD=BC,DC=AB,AE=CF,找出图中的一对全等三角形,并说明你的理由。
3 探索三角形全等的条件(2)
【学习目标】
1、探索出三角形全等的条件“ASA”和“AAS”并能应用它们来判定两个三角形
是否全等。
2、体会利用转化的数学思想和方法解决问题的过程。
3、能够有条理的思考和理解简单的推理过程,并运用数学语言说明问题。
4、敢于面对数学活动中的困难,并能通过合作交流解决遇到的问题。
【自主学习】
两角和它们的夹边对应相等的两个三角形全等,简写成“_______”或“_____”.
两角和其中一角的对边对应相等的两个三角形全等.简写成“_______”或“_____”.
【合作探究】
1、如图,已知AB=DE,∠A =∠D,∠B=∠E,则△ABC≌△DEF的理由是:___________
2、如图,已知AB=DE ,∠A=∠D,∠C=∠F,则△ABC≌△DEF的理由是:____________
3.图中的两个三角形全等吗 请说明理由.
解:在△ABC和△DBC中
∠___=∠___
∠___=∠___
____=____
△ABC≌△DBC
【精讲点拨】
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
【巩固检测】
1.如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
A.BD=AD B.AB=AC C.∠1=∠2 D.以上答案都不对
2.如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是_____________。
3.如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=
4.如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC。
3 探索三角形全等的条件(3)
【学习目标】
明确SAS公理的内容,能用SAS证明两个三角形全等。
通过SAS公理的运用提高学生的逻辑思维能力,通过观察几何图形培养学生识图能力和应用数学知识解决实际问题的能力。
【自主学习】
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?说说怎么做?
________________________的两个三角形全等。(或___________)
【合作探究】
如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件 .
【精讲点拨】
如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需增加的条件是 .
.
【巩固检测】
1. 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是( )A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
2.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
3.已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
2
【学习目标】
1.经历探索三角形全等的“边边边”的条件的过程.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
【自主学习】
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
1.作图方法:
先画一线段AB,使得AB=6cm,再分别以A、B为圆心,8cm、10cm为半径画弧,两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=6cm,AC=8cm,BC=10cm.
2.以小组为单位,把剪下的三角形重叠在一起,发现都能够重合.这说明这些三角形都是全等的.
这反映了一个规律:
_______________的两个三角形全等,简写为_________或_________.
用三根木条钉成三角形框架,它的大小和形状是固定不变的,而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的__________.
【合作探究】
如图,1、如图,△ABC中 AB=AC, D为BC中点
求证:①△ABD≌△ACD.
②∠BAD=∠CAD
③AD⊥BC
证明:
【精讲点拨】
如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC.∠B与∠E相等吗?为什么?
【巩固检测】
1.如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的AB,CD两根木条),这样做是运用了三角形的( )
A.全等性 B.灵活性 C.稳定性 D.对称性
2.如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,AB=CD,AD=CB,那么下列结论中错误的是( )
A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD
4.如图,AD=BC,DC=AB,AE=CF,找出图中的一对全等三角形,并说明你的理由。
3 探索三角形全等的条件(2)
【学习目标】
1、探索出三角形全等的条件“ASA”和“AAS”并能应用它们来判定两个三角形
是否全等。
2、体会利用转化的数学思想和方法解决问题的过程。
3、能够有条理的思考和理解简单的推理过程,并运用数学语言说明问题。
4、敢于面对数学活动中的困难,并能通过合作交流解决遇到的问题。
【自主学习】
两角和它们的夹边对应相等的两个三角形全等,简写成“_______”或“_____”.
两角和其中一角的对边对应相等的两个三角形全等.简写成“_______”或“_____”.
【合作探究】
1、如图,已知AB=DE,∠A =∠D,∠B=∠E,则△ABC≌△DEF的理由是:___________
2、如图,已知AB=DE ,∠A=∠D,∠C=∠F,则△ABC≌△DEF的理由是:____________
3.图中的两个三角形全等吗 请说明理由.
解:在△ABC和△DBC中
∠___=∠___
∠___=∠___
____=____
△ABC≌△DBC
【精讲点拨】
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
【巩固检测】
1.如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
A.BD=AD B.AB=AC C.∠1=∠2 D.以上答案都不对
2.如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是_____________。
3.如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=
4.如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC。
3 探索三角形全等的条件(3)
【学习目标】
明确SAS公理的内容,能用SAS证明两个三角形全等。
通过SAS公理的运用提高学生的逻辑思维能力,通过观察几何图形培养学生识图能力和应用数学知识解决实际问题的能力。
【自主学习】
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?说说怎么做?
________________________的两个三角形全等。(或___________)
【合作探究】
如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件 .
【精讲点拨】
如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需增加的条件是 .
.
【巩固检测】
1. 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是( )A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
2.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
3.已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
2
