鲁教版(五四学制)七年级数学上册 第一章三角形复习学案(无答案)
文档属性
| 名称 | 鲁教版(五四学制)七年级数学上册 第一章三角形复习学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 00:00:00 | ||
图片预览

文档简介
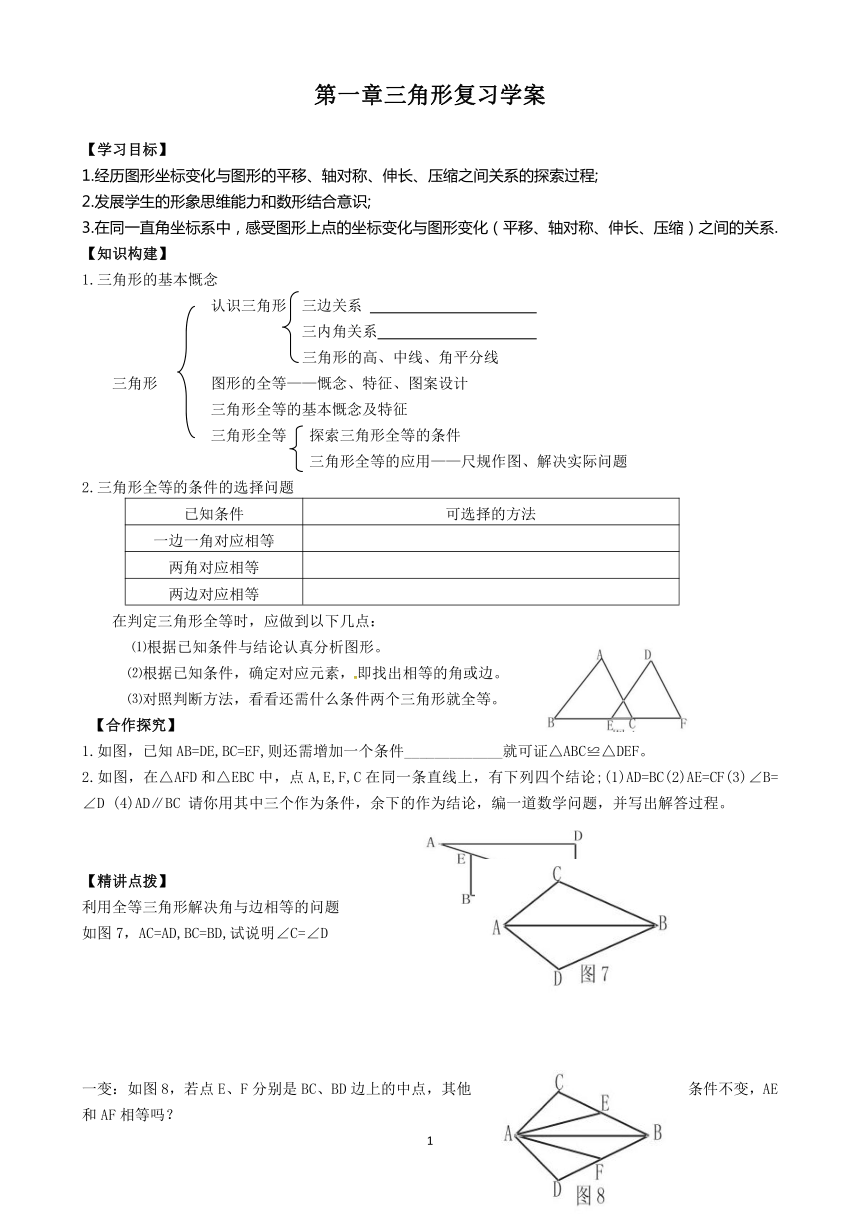
第一章三角形复习学案
【学习目标】
1.经历图形坐标变化与图形的平移、轴对称、伸长、压缩之间关系的探索过程;
2.发展学生的形象思维能力和数形结合意识;
3.在同一直角坐标系中,感受图形上点的坐标变化与图形变化(平移、轴对称、伸长、压缩)之间的关系.
【知识构建】
1.三角形的基本慨念
认识三角形 三边关系
三内角关系
三角形的高、中线、角平分线
三角形 图形的全等——慨念、特征、图案设计
三角形全等的基本慨念及特征
三角形全等 探索三角形全等的条件
三角形全等的应用——尺规作图、解决实际问题[来源:学
2.三角形全等的条件的选择问题
已知条件 可选择的方法
一边一角对应相等
两角对应相等
两边对应相等
在判定三角形全等时,应做到以下几点:
⑴根据已知条件与结论认真分析图形。
⑵根据已知条件,确定对应元素,即找出相等的角或边。
⑶对照判断方法,看看还需什么条件两个三角形就全等。
【合作探究】
1.如图,已知AB=DE,BC=EF,则还需增加一个条件_____________就可证△ABC≌△DEF。
2.如图,在△AFD和△EBC中,点A,E,F,C在同一条直线上,有下列四个结论;(1)AD=BC(2)AE=CF(3)∠B=∠D (4)AD∥BC 请你用其中三个作为条件,余下的作为结论,编一道数学问题,并写出解答过程。
【精讲点拨】
利用全等三角形解决角与边相等的问题
如图7,AC=AD,BC=BD,试说明∠C=∠D
一变:如图8,若点E、F分别是BC、BD边上的中点,其他条件不变,AE和AF相等吗?
二变:如图9若连接CD,且CD与AB相交于点P,请你说明AB与CD有何关系?为什么?
【巩固检测】
1.在 ABC中, A=30 , B=2 C,则 C=______度, B=______度.
2.一个三角形的三边长分别是3,4,,则的取值范围是( )
A.>3 B.>4 C.3<<4 D.1<<7
3.如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC, BC、DE交于点O.
求证:(1) △ABC≌△AED; (2) OB=OE .
2
【学习目标】
1.经历图形坐标变化与图形的平移、轴对称、伸长、压缩之间关系的探索过程;
2.发展学生的形象思维能力和数形结合意识;
3.在同一直角坐标系中,感受图形上点的坐标变化与图形变化(平移、轴对称、伸长、压缩)之间的关系.
【知识构建】
1.三角形的基本慨念
认识三角形 三边关系
三内角关系
三角形的高、中线、角平分线
三角形 图形的全等——慨念、特征、图案设计
三角形全等的基本慨念及特征
三角形全等 探索三角形全等的条件
三角形全等的应用——尺规作图、解决实际问题[来源:学
2.三角形全等的条件的选择问题
已知条件 可选择的方法
一边一角对应相等
两角对应相等
两边对应相等
在判定三角形全等时,应做到以下几点:
⑴根据已知条件与结论认真分析图形。
⑵根据已知条件,确定对应元素,即找出相等的角或边。
⑶对照判断方法,看看还需什么条件两个三角形就全等。
【合作探究】
1.如图,已知AB=DE,BC=EF,则还需增加一个条件_____________就可证△ABC≌△DEF。
2.如图,在△AFD和△EBC中,点A,E,F,C在同一条直线上,有下列四个结论;(1)AD=BC(2)AE=CF(3)∠B=∠D (4)AD∥BC 请你用其中三个作为条件,余下的作为结论,编一道数学问题,并写出解答过程。
【精讲点拨】
利用全等三角形解决角与边相等的问题
如图7,AC=AD,BC=BD,试说明∠C=∠D
一变:如图8,若点E、F分别是BC、BD边上的中点,其他条件不变,AE和AF相等吗?
二变:如图9若连接CD,且CD与AB相交于点P,请你说明AB与CD有何关系?为什么?
【巩固检测】
1.在 ABC中, A=30 , B=2 C,则 C=______度, B=______度.
2.一个三角形的三边长分别是3,4,,则的取值范围是( )
A.>3 B.>4 C.3<<4 D.1<<7
3.如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC, BC、DE交于点O.
求证:(1) △ABC≌△AED; (2) OB=OE .
2
