人教A版2019选择性必修第二册第五章 一元函数的导数及其应用 同步单元必刷卷(基础版)(Word版含解析)
文档属性
| 名称 | 人教A版2019选择性必修第二册第五章 一元函数的导数及其应用 同步单元必刷卷(基础版)(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 00:00:00 | ||
图片预览





文档简介
第五章:一元函数的导数及其应用同步单元必刷卷(基础版)
(时间:120分钟 满分:150分)
单项选择题(本大题共8小题,每小题5分,共40分)
1.(2022·江苏·高二课时练习)一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.(2022·福建省漳州第一中学高二月考)设为可导函数,且当时,,则曲线在点处的切线斜率为( )
A.2 B. C.1 D.
3.(2022·全国·高二课时练习)下列关于函数的复合过程与导数运算正确的是( )
A.,, B.,,
C.,, D.,,
4.(2022·重庆市清华中学校高二月考)若函数在区间内存在单调递增区间,则实数的取值范围是( )
A. B. C. D.
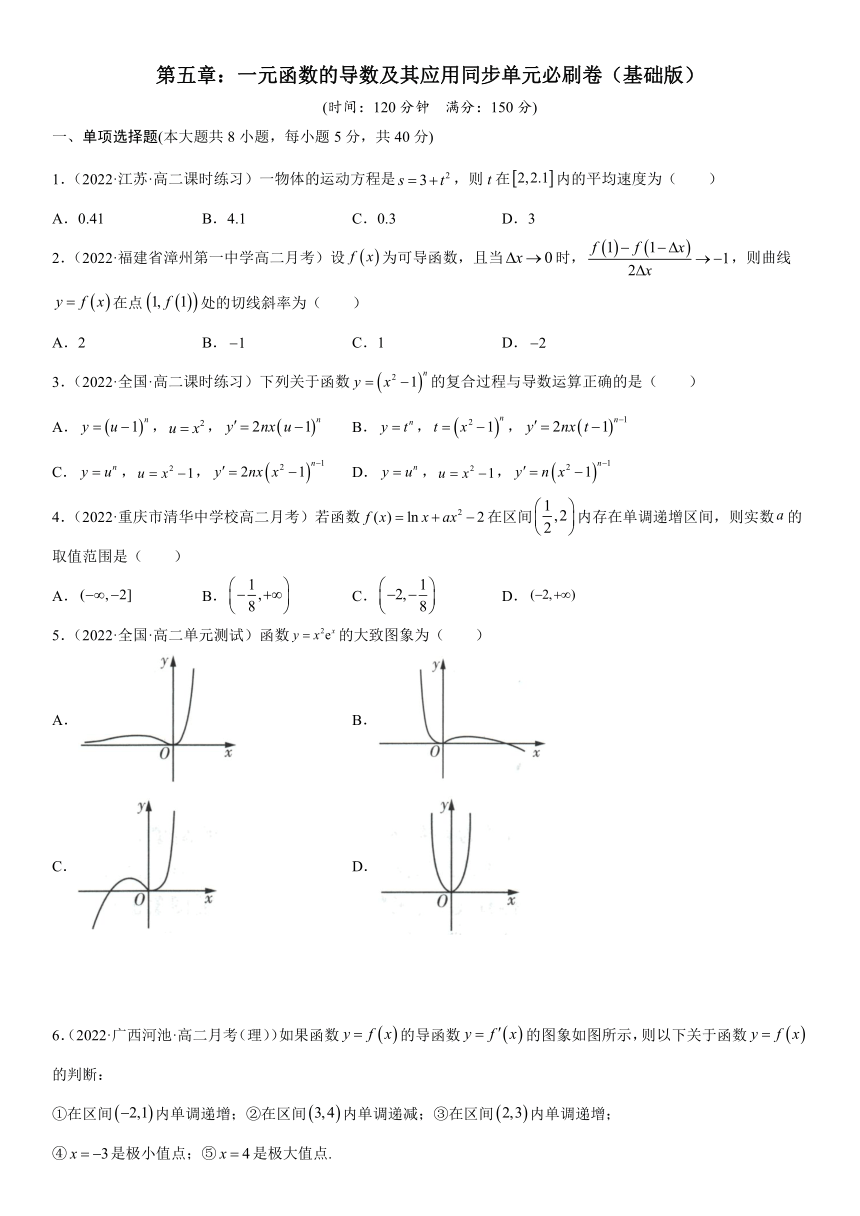
5.(2022·全国·高二单元测试)函数的大致图象为( )
A. B.
C. D.
6.(2022·广西河池·高二月考(理))如果函数的导函数的图象如图所示,则以下关于函数的判断:
①在区间内单调递增;②在区间内单调递减;③在区间内单调递增;
④是极小值点;⑤是极大值点.
其中不正确的是( )
A.③⑤ B.②③ C.①④⑤ D.①②④
7.(2022·福建省漳州第一中学高二月考)已知函数,要使函数的零点个数最多,则k的取值范围是( )
A. B. C. D.
8.(2022·江苏·高二课时练习)已知函数f(x)=x2lnx,,若x>0时,恒成立,则实数a的取值范围是( )
A.[-1,1] B.[-1,+∞)
C.(-∞,-1] D.(-∞,-1]∪[1,+∞)
多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.(2022·全国·高二专题练习)已知函数,则下列说法正确的是( )
A.只有一个极值点 B.设,则与的单调性相同
C.在上单调递增 D.有且只有两个零点
10.(2022·河北·藁城新冀明中学高二月考)若是函数的极值点,则下列结论不正确的是( )
A.有极大值-1 B.有极小值-1
C.有极大值0 D.有极小值0
11.(2022·全国·高二课时练习)设函数,则( )
A.有极大值,且有最大值 B.有极小值,且有最小值
C.若方程恰有一个实根,则 D.若方程恰有三个实根,则
12.(2022·全国·高二课时练习)已知函数且函数g(x)=xf(x),则下列选项正确的是( )
A. x1∈(0,1),x2∈(1,3),使f(x1)>f(x2)
B.点(0,0)是函数f(x)的零点
C.函数f(x)的值域为
D.若关于x的方程[g(x)]2﹣2ag(x)=0有两个不相等的实数根,则实数a的取值范围是
三、填空题(本大题共4小题,每小题5分,共20分)
13.(2022·广东·徐闻县第一中学高二期中)函数的图象在点处的切线方程为___________.
14.(2022·全国·高二课时练习)若函数在区间上具有单调性,则a的取值范围是________.
15.(2022·全国·高二课时练习)如图所示,一窗户的上部分是半圆,下半部分是矩形,如果窗户面积一定,窗户周长最小时,h与x的比为______.
16.(2022·全国·高二课时练习)若的图像上存在两点关于原点对称,则点对称为函数的“友情点对”(点对与视为同一个“友情点对”.)若,恰有两个“友情点对”,则实数的取值范围是___________.
四、解答题(本大题共6小题,共70分)
17.(2022·广东实验中学附属天河学校高二月考)已知函数的图象在点处的切线斜率为,且时,有极值.
(1)求的解析式;
(2)求在上的最大值和最小值.
18.(2022·重庆巴蜀中学高二开学考试)已知函数f(x)=x+,g(x)=2x+a.
(1)求函数f(x)=x+在上的值域;
(2)若 x1∈, x2∈[2,3],使得f(x1)≥g(x2),求实数a的取值范围.
19.(2022·全国·高二单元测试)已知函数.
(1)讨论的单调性;
(2)若函数在上有零点,求的取值范围.
20.(2022·全国·高二课时练习)已知函数.
(1)讨论函数的单调性;
(2)当时,设函数的两个零点为,,试证明:.
21.(2022·吉林·延边二中高二期中(理))已知函数.
(1)若存在极值,求的取值范围;
(2)当时,求证:.
22.(2022·吉林·松原市实验高级中学高二月考)已知函数.
(1)讨论函数在区间上的最小值;
(2)当时,求证:对任意,恒有成立.
第五章:一元函数的导数及其应用同步单元必刷卷(基础版)全解全析
1.B
【详解】
,
故选:B
2.D
【分析】
由导数的定义及导数的几何意义即可求解.
【详解】
解:由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
故选:D.
3.C
【分析】
直接根据函数的结构,找到内层函数和外层函数,即可得解.
【详解】
由复合函数求导法则,知函数由基本初等函数,复合而成,
所以.
故选:C.
4.D
【分析】
求出函数的导数,问题转化为 而 在 递增,求出 的最小值,从而求出的范围即可 .
【详解】
若在区间内存在单调递增区间,则有解,
故
令
在递增 ,
故
故选:D
5.A
【分析】
求导分析函数单调性,并根据函数的正负判断即可.
【详解】
由题意可知,
当或时,,当时,,
所以在和上单调递增,在上单调递减,且当时,.
故选:A.
6.A
【分析】
根据导函数与单调性和极值点的关系,观察图像即可得出答案.
【详解】
由图可知,
在区间内,有正有负,①错误;
在区间内,,在区间内单调递增,②错误;
在区间内,,在区间内单调递增,③正确;
不存在,使当时,,当时,,④错误;
存在,使当时,,当时,,如,⑤正确
故选:A.
7.B
【分析】
利用导数判断函数的单调性,根据单调性可得,当时,有2个不等实根;时,有1个不等实根,又因为,对称轴,所以当方程有两个根,一个在,之间,一个大于0时的零点最多为3个,根据一元二次方程根的分布列不等式组求解即可得答案.
【详解】
解:因为,所以,
令得,得,
所以在上单调递减,在单调递增,
所以有最小值,且时,,
令,则时,有2个不等实根;时,有1个不等实根,
要使函数的零点个数最多,
则方程在,上的根最多,
因为,对称轴,所以的零点最多为3个,
此时方程有两个根,一个在,之间,一个大于0,
所以,解得,
故选:B.
8.A
【分析】
当时,恒成立可得,当时,构造函数,利用导数探讨其单调性并确定a的范围即可作答..
【详解】
依题意,当时,有恒成立,而有,则,即,解得,
当时,有恒成立,即,
令,求导得,令,,
则有在单调递增,,若,而,则必存在使得,
当时,,则在上单调递减,于是有与当时,恒成立矛盾,
从而得,解得,而当时,,,在上单调递增,恒成立,则,
综上得,,
所以实数a的取值范围是.
故选:A
【点睛】
结论点睛:对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立 a≥f(x)max;(2)a≤f(x)恒成立 a≤ f(x)min.
9.ACD
【分析】
利用的二次求导,得到, ,从而存在,使得,结合函数极值点的定义即可判断选项,求出的解析式,然后利用导数研究其单调性即可判断选项,利用函数单调性的结论即可判断选项.利用函数的极值点即可判断选项.
【详解】
解:由题知,,,所以在上单调递增,当时,;当时,,所以存在,使得,所以函数在上单调递减,在上单调递增,所以有且只有一个极值点,故A正确;
因为,所以,所以,所以,故的一个极值点为0,所以与的单调性不相同,故B错误;
因为与在上都是单调递增,所以在上单调递增,故C正确;
因为有且只有一个极值点,,且,所以在和上各有一个零点,所以有且只有两个零点,故D正确.
故选:ACD.
10.BCD
【分析】
先根据极值定义得a,再求导函数零点,根据导函数符号变化规律确定极值.
【详解】
解:因为是函数的极值点,所以 ,
当时,当时,因此有极大值,无极小值
故选:BCD.
11.BD
【分析】
求出函数的导数,讨论其符号可得函数的单调性和最值,据此可刻画出函数的图象,从而可得正确的选项.
【详解】
由题意,得,
∴当或时,,当时,,
∴在和上单调递增,在上单调递减,
∴有极大值,为,有极小值,为.
又当时,恒成立,∴也是最小值.
作出直线和的图象,如图所示,
当或时,有一个实根,当时,有三个实根.
故选:BD.
12.AC
【分析】
A选项,分别求出f(x)在区间(0,1)和(1,3)的值域,通过值域的包含关系判断;
B选项,利用零点的概念判断;
C选项,分别求出f(x)在区间(﹣∞,1)和(1,+∞)的值域,取并集即可.
D选项,题意等价于方程g(x)=2a只有一个非零实数根,根据g(x)的单调性及极值判断.
【详解】
解:A选项,设h(x)=xex,h'(x)=(x+1)ex,所以h(x)在(0,1)单调递增,h(x)∈(0,e);
设m(x)=,m'(x)=,所以m(x)在(1,3)上递减,m(x)∈(,e) (0,e),所以A说法正确;
B选项,x=0是函数f(x)的零点,B说法错误;
C选项,h(x)=xex在(﹣∞,﹣1)上递减,(﹣1,1)上递增,又当x<0时,h(x)<0,且h(﹣1)=,所以h(x)的值域为.
m(x)=在(1,3)上递减,(3,+∞)上递增,所以m(x)的值域为[,+∞),所以f(x)的值域为[,+∞),C选项正确.
D选项,[g(x)]2﹣2ag(x)=0等价于g(x)=2a或g(x)=0.
因为当g(x)=0,即f(x)=0时,解得x=0,所以方程g(x)=2a只有一个非零实数根.
因为,所以g(x)在(﹣∞,﹣2)上单调递增,(﹣2,0)上单调递减,(0,1)上单调递增,(1,2)上单调递减,(2,+∞)上单调递增.
当x<0是,g(x)>0,且g(﹣2)=,g(0)=0,g(1)=e,g(2)=e,
解得或,D选项说法错误.
故选:AC.
13.
【分析】
利用导数的几何意义可求得切线斜率,结合切点坐标可得切线方程.
【详解】
由题意得:,则,又,
切线方程为,即.
故答案为:.
14.
【分析】
对函数求导,将函数在区间上具有单调性,转化为在区间恒大于0,或恒小于0,进而求出a的取值范围
【详解】
,函数在区间上具有单调性等价于或在上恒成立,
则或,设,
当时,取得最大值,,当时,取得最小值,
所以或.
故答案为:
15.
【分析】
将周长用x表示出来,再利用导数求函数的最值,进而得出比例.
【详解】
解:设窗户面积为S,周长为L,则,,
所以窗户周长,
则,由,得,
故当时,;
当时,,
所以当时,L取最小值,
此时.
故答案为:.
16.
【分析】
要求“友情对点”,可把的函数图像关于原点对称,即研究对称过去的图像和的图像有两个交点即可.
【详解】
解:关于原点对称的解析式为.
的图像与的交点个数即为方程根的个数,即.
设,于是
当时,,单调递减;
当时,,单调递增;
当时,函数取最小值.
于是作出的图像如图所示.
,即时与有两个交点,原函数有两对“友情对点”.故实数的取值范围是
故答案为:
17.(1);(2)最大值为8,最小值为.
【分析】
(1)先对函数求导,然后利用导数的几何意义可得从而可求出的值,进而可得的解析式;
(2)先对函数求导,然后令导数等于零,求出极值点,再求出极值和端点处的函数值,比较可得函数的最值
【详解】
解:(1)由题意可得,.
由解得
经检验得时,有极大值.
所以.
(2)由(1)知,.
令,得,,
,的值随的变化情况如下表:
2
0 0
单调递增 极大值 单调递减 极小值 单调递增
函数值 3 8 8
由表可知在上的最大值为8,最小值为.
18.(1);(2).
【分析】
(1)先求导数,判断函数单调性,结合单调性求解值域;
(2)把条件转化为,分别求解的最小值可得实数a的范围.
【详解】
(1),
因为,所以,即函数为减函数,
因为,所以值域为.
(2)因为 x1∈, x2∈[2,3],使得f(x1)≥g(x2),
所以,
因为,所以,
所以,即.
19.(1)见解析;(2)
【分析】
(1)先求导,对a分类讨论,利用导函数的正负可得f(x)的单调性.
(2)将已知进行转化,得到在上有解,分离参数a,构造函数,求导求得值域,可得a的范围.
【详解】
(1)因为,所以.
①当时,因为,所以在上单调递增;
②当时,令,解得或.
令,解得,
则在,上单调递增;
在上单调递减.
(2)因为,所以,
在上有零点,等价于关于的方程在上有解,
即在上有解.
因为,所以.
令,则.
令,,解得;令,,解得,
则 上单调递减,在上单调递增,
因为 ,,
所以 ,
则, ,
故的取值范围为.
【点睛】
本题考查了利用导数研究函数的单调性与零点问题,考查了函数的最值的求法,考查了等价转化方法,考查了推理能力与计算能力,属于难题.
20.(1)当时,在上单调递增;
当时,在上单调递增,在上单调递减;
(2)证明见解析.
【分析】
(1)求出导函数,讨论的取值范围,利用导数与函数单调性之间的关系即可求解.
(2)利用导数求出函数的极大值,由零点存在性定理可得两零点所在的区间,不妨设,则有,构造函数,,利用导数判断出函数单调递增,从而可得,再由即可求解.
【详解】
解:(1)易得函数的定义域为.
对函数求导得:.
当时,恒成立,即可知在上单调递增;
当时,当时,,当时,,
故在上单调递增,在上单调递减.
(2)当时,,,
此时在上单调递增,在上单调递减.
,又,,
不妨设,则有,
令,,
.
当时,,单调递增,
,,
,
又,,
,,在上单调递减,
,即.
【点睛】
本题考查了利用导数研究函数的单调性、利用导数证明不等式,属于难题.
21.(1);(2)证明见解析.
【分析】
(1)对函数求导,分和两种情况,分别判断出函数的单调性与极值,可得的取值范围;
(2)当时,设,成立,即证明,对函数求导判断出单调性和最值,可得命题成立.
【详解】
(1)函数的定义域为,
,
当时,对任意的,,
故在上单调递增,无极值;
当时,当时,,单调递增;
当时,,单调递减.
故在处取得极大值,无极小值.
综上所述,若存在极值,则的取值范围为.
(2)当时,.
设,其定义域为,
则证明即可.
,设,
则,
故函数在上单调递增.
,.
有唯一的实根,且,
.
当时,;
当时,,
故函数的最小值为.
.
.
【点睛】
关键点点睛:本题考查导数解决函数的单调性问题,考查导数证明不等式,解决本题的关键点是构造,将命题成立,转化为证明,对函数求导判断出单调性和最值,可得命题成立,考查学生逻辑推理能力和计算能力,属于中档题.
22.(1)答案见解析;(2)证明见解析.
【分析】
(1)先求出函数的定义域,再求导,当时,导数恒小于零,则可得函数在上为减函数,从而可求出函数的最小值,当时,由导数可得函数在上单调递减,在上单调递增,然后分,和三种情况讨论可求得函数的最小值;
(2)要证,即证,即证,当时,上式恒成立,当时,令,再利用导数可得,从而可得成立.
【详解】
(1)解:函数的定义域是,
.
①当时,,则,
则函数在上单调递减,即函数在区间上单调递减,
故函数在区间上的最小值为.
②当时,令,得;令,得;
故函数在上单调递减,在上单调递增.
(i)当,即时,函数在区间上单调递增,故函数在区间上的最小值为;
(ii)当,即时,函数在区间上单调递减,故函数在区间上的最小值为;
(iii)当,即时,函数在上单调递减,在上单调递增,此时函数在区间上的最小值为.
综上,当时,函数在区间上的最小值为;当时,函数在区间上的最小值为;当时,函数在区间上的最小值为.
(2)证明:当时,,
要证,即证,
因为,所以两边同时乘x,得,
即证.
当时,,而,
所以成立,即成立.
当时,令,
则.
设,,则因为.
因为,所以,
所以当时,单调递增,
所以,即,
所以在上单调递增,
所以,即成立.
综上,对任意,恒有成立.
(时间:120分钟 满分:150分)
单项选择题(本大题共8小题,每小题5分,共40分)
1.(2022·江苏·高二课时练习)一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.(2022·福建省漳州第一中学高二月考)设为可导函数,且当时,,则曲线在点处的切线斜率为( )
A.2 B. C.1 D.
3.(2022·全国·高二课时练习)下列关于函数的复合过程与导数运算正确的是( )
A.,, B.,,
C.,, D.,,
4.(2022·重庆市清华中学校高二月考)若函数在区间内存在单调递增区间,则实数的取值范围是( )
A. B. C. D.
5.(2022·全国·高二单元测试)函数的大致图象为( )
A. B.
C. D.
6.(2022·广西河池·高二月考(理))如果函数的导函数的图象如图所示,则以下关于函数的判断:
①在区间内单调递增;②在区间内单调递减;③在区间内单调递增;
④是极小值点;⑤是极大值点.
其中不正确的是( )
A.③⑤ B.②③ C.①④⑤ D.①②④
7.(2022·福建省漳州第一中学高二月考)已知函数,要使函数的零点个数最多,则k的取值范围是( )
A. B. C. D.
8.(2022·江苏·高二课时练习)已知函数f(x)=x2lnx,,若x>0时,恒成立,则实数a的取值范围是( )
A.[-1,1] B.[-1,+∞)
C.(-∞,-1] D.(-∞,-1]∪[1,+∞)
多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.(2022·全国·高二专题练习)已知函数,则下列说法正确的是( )
A.只有一个极值点 B.设,则与的单调性相同
C.在上单调递增 D.有且只有两个零点
10.(2022·河北·藁城新冀明中学高二月考)若是函数的极值点,则下列结论不正确的是( )
A.有极大值-1 B.有极小值-1
C.有极大值0 D.有极小值0
11.(2022·全国·高二课时练习)设函数,则( )
A.有极大值,且有最大值 B.有极小值,且有最小值
C.若方程恰有一个实根,则 D.若方程恰有三个实根,则
12.(2022·全国·高二课时练习)已知函数且函数g(x)=xf(x),则下列选项正确的是( )
A. x1∈(0,1),x2∈(1,3),使f(x1)>f(x2)
B.点(0,0)是函数f(x)的零点
C.函数f(x)的值域为
D.若关于x的方程[g(x)]2﹣2ag(x)=0有两个不相等的实数根,则实数a的取值范围是
三、填空题(本大题共4小题,每小题5分,共20分)
13.(2022·广东·徐闻县第一中学高二期中)函数的图象在点处的切线方程为___________.
14.(2022·全国·高二课时练习)若函数在区间上具有单调性,则a的取值范围是________.
15.(2022·全国·高二课时练习)如图所示,一窗户的上部分是半圆,下半部分是矩形,如果窗户面积一定,窗户周长最小时,h与x的比为______.
16.(2022·全国·高二课时练习)若的图像上存在两点关于原点对称,则点对称为函数的“友情点对”(点对与视为同一个“友情点对”.)若,恰有两个“友情点对”,则实数的取值范围是___________.
四、解答题(本大题共6小题,共70分)
17.(2022·广东实验中学附属天河学校高二月考)已知函数的图象在点处的切线斜率为,且时,有极值.
(1)求的解析式;
(2)求在上的最大值和最小值.
18.(2022·重庆巴蜀中学高二开学考试)已知函数f(x)=x+,g(x)=2x+a.
(1)求函数f(x)=x+在上的值域;
(2)若 x1∈, x2∈[2,3],使得f(x1)≥g(x2),求实数a的取值范围.
19.(2022·全国·高二单元测试)已知函数.
(1)讨论的单调性;
(2)若函数在上有零点,求的取值范围.
20.(2022·全国·高二课时练习)已知函数.
(1)讨论函数的单调性;
(2)当时,设函数的两个零点为,,试证明:.
21.(2022·吉林·延边二中高二期中(理))已知函数.
(1)若存在极值,求的取值范围;
(2)当时,求证:.
22.(2022·吉林·松原市实验高级中学高二月考)已知函数.
(1)讨论函数在区间上的最小值;
(2)当时,求证:对任意,恒有成立.
第五章:一元函数的导数及其应用同步单元必刷卷(基础版)全解全析
1.B
【详解】
,
故选:B
2.D
【分析】
由导数的定义及导数的几何意义即可求解.
【详解】
解:由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
故选:D.
3.C
【分析】
直接根据函数的结构,找到内层函数和外层函数,即可得解.
【详解】
由复合函数求导法则,知函数由基本初等函数,复合而成,
所以.
故选:C.
4.D
【分析】
求出函数的导数,问题转化为 而 在 递增,求出 的最小值,从而求出的范围即可 .
【详解】
若在区间内存在单调递增区间,则有解,
故
令
在递增 ,
故
故选:D
5.A
【分析】
求导分析函数单调性,并根据函数的正负判断即可.
【详解】
由题意可知,
当或时,,当时,,
所以在和上单调递增,在上单调递减,且当时,.
故选:A.
6.A
【分析】
根据导函数与单调性和极值点的关系,观察图像即可得出答案.
【详解】
由图可知,
在区间内,有正有负,①错误;
在区间内,,在区间内单调递增,②错误;
在区间内,,在区间内单调递增,③正确;
不存在,使当时,,当时,,④错误;
存在,使当时,,当时,,如,⑤正确
故选:A.
7.B
【分析】
利用导数判断函数的单调性,根据单调性可得,当时,有2个不等实根;时,有1个不等实根,又因为,对称轴,所以当方程有两个根,一个在,之间,一个大于0时的零点最多为3个,根据一元二次方程根的分布列不等式组求解即可得答案.
【详解】
解:因为,所以,
令得,得,
所以在上单调递减,在单调递增,
所以有最小值,且时,,
令,则时,有2个不等实根;时,有1个不等实根,
要使函数的零点个数最多,
则方程在,上的根最多,
因为,对称轴,所以的零点最多为3个,
此时方程有两个根,一个在,之间,一个大于0,
所以,解得,
故选:B.
8.A
【分析】
当时,恒成立可得,当时,构造函数,利用导数探讨其单调性并确定a的范围即可作答..
【详解】
依题意,当时,有恒成立,而有,则,即,解得,
当时,有恒成立,即,
令,求导得,令,,
则有在单调递增,,若,而,则必存在使得,
当时,,则在上单调递减,于是有与当时,恒成立矛盾,
从而得,解得,而当时,,,在上单调递增,恒成立,则,
综上得,,
所以实数a的取值范围是.
故选:A
【点睛】
结论点睛:对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立 a≥f(x)max;(2)a≤f(x)恒成立 a≤ f(x)min.
9.ACD
【分析】
利用的二次求导,得到, ,从而存在,使得,结合函数极值点的定义即可判断选项,求出的解析式,然后利用导数研究其单调性即可判断选项,利用函数单调性的结论即可判断选项.利用函数的极值点即可判断选项.
【详解】
解:由题知,,,所以在上单调递增,当时,;当时,,所以存在,使得,所以函数在上单调递减,在上单调递增,所以有且只有一个极值点,故A正确;
因为,所以,所以,所以,故的一个极值点为0,所以与的单调性不相同,故B错误;
因为与在上都是单调递增,所以在上单调递增,故C正确;
因为有且只有一个极值点,,且,所以在和上各有一个零点,所以有且只有两个零点,故D正确.
故选:ACD.
10.BCD
【分析】
先根据极值定义得a,再求导函数零点,根据导函数符号变化规律确定极值.
【详解】
解:因为是函数的极值点,所以 ,
当时,当时,因此有极大值,无极小值
故选:BCD.
11.BD
【分析】
求出函数的导数,讨论其符号可得函数的单调性和最值,据此可刻画出函数的图象,从而可得正确的选项.
【详解】
由题意,得,
∴当或时,,当时,,
∴在和上单调递增,在上单调递减,
∴有极大值,为,有极小值,为.
又当时,恒成立,∴也是最小值.
作出直线和的图象,如图所示,
当或时,有一个实根,当时,有三个实根.
故选:BD.
12.AC
【分析】
A选项,分别求出f(x)在区间(0,1)和(1,3)的值域,通过值域的包含关系判断;
B选项,利用零点的概念判断;
C选项,分别求出f(x)在区间(﹣∞,1)和(1,+∞)的值域,取并集即可.
D选项,题意等价于方程g(x)=2a只有一个非零实数根,根据g(x)的单调性及极值判断.
【详解】
解:A选项,设h(x)=xex,h'(x)=(x+1)ex,所以h(x)在(0,1)单调递增,h(x)∈(0,e);
设m(x)=,m'(x)=,所以m(x)在(1,3)上递减,m(x)∈(,e) (0,e),所以A说法正确;
B选项,x=0是函数f(x)的零点,B说法错误;
C选项,h(x)=xex在(﹣∞,﹣1)上递减,(﹣1,1)上递增,又当x<0时,h(x)<0,且h(﹣1)=,所以h(x)的值域为.
m(x)=在(1,3)上递减,(3,+∞)上递增,所以m(x)的值域为[,+∞),所以f(x)的值域为[,+∞),C选项正确.
D选项,[g(x)]2﹣2ag(x)=0等价于g(x)=2a或g(x)=0.
因为当g(x)=0,即f(x)=0时,解得x=0,所以方程g(x)=2a只有一个非零实数根.
因为,所以g(x)在(﹣∞,﹣2)上单调递增,(﹣2,0)上单调递减,(0,1)上单调递增,(1,2)上单调递减,(2,+∞)上单调递增.
当x<0是,g(x)>0,且g(﹣2)=,g(0)=0,g(1)=e,g(2)=
解得或,D选项说法错误.
故选:AC.
13.
【分析】
利用导数的几何意义可求得切线斜率,结合切点坐标可得切线方程.
【详解】
由题意得:,则,又,
切线方程为,即.
故答案为:.
14.
【分析】
对函数求导,将函数在区间上具有单调性,转化为在区间恒大于0,或恒小于0,进而求出a的取值范围
【详解】
,函数在区间上具有单调性等价于或在上恒成立,
则或,设,
当时,取得最大值,,当时,取得最小值,
所以或.
故答案为:
15.
【分析】
将周长用x表示出来,再利用导数求函数的最值,进而得出比例.
【详解】
解:设窗户面积为S,周长为L,则,,
所以窗户周长,
则,由,得,
故当时,;
当时,,
所以当时,L取最小值,
此时.
故答案为:.
16.
【分析】
要求“友情对点”,可把的函数图像关于原点对称,即研究对称过去的图像和的图像有两个交点即可.
【详解】
解:关于原点对称的解析式为.
的图像与的交点个数即为方程根的个数,即.
设,于是
当时,,单调递减;
当时,,单调递增;
当时,函数取最小值.
于是作出的图像如图所示.
,即时与有两个交点,原函数有两对“友情对点”.故实数的取值范围是
故答案为:
17.(1);(2)最大值为8,最小值为.
【分析】
(1)先对函数求导,然后利用导数的几何意义可得从而可求出的值,进而可得的解析式;
(2)先对函数求导,然后令导数等于零,求出极值点,再求出极值和端点处的函数值,比较可得函数的最值
【详解】
解:(1)由题意可得,.
由解得
经检验得时,有极大值.
所以.
(2)由(1)知,.
令,得,,
,的值随的变化情况如下表:
2
0 0
单调递增 极大值 单调递减 极小值 单调递增
函数值 3 8 8
由表可知在上的最大值为8,最小值为.
18.(1);(2).
【分析】
(1)先求导数,判断函数单调性,结合单调性求解值域;
(2)把条件转化为,分别求解的最小值可得实数a的范围.
【详解】
(1),
因为,所以,即函数为减函数,
因为,所以值域为.
(2)因为 x1∈, x2∈[2,3],使得f(x1)≥g(x2),
所以,
因为,所以,
所以,即.
19.(1)见解析;(2)
【分析】
(1)先求导,对a分类讨论,利用导函数的正负可得f(x)的单调性.
(2)将已知进行转化,得到在上有解,分离参数a,构造函数,求导求得值域,可得a的范围.
【详解】
(1)因为,所以.
①当时,因为,所以在上单调递增;
②当时,令,解得或.
令,解得,
则在,上单调递增;
在上单调递减.
(2)因为,所以,
在上有零点,等价于关于的方程在上有解,
即在上有解.
因为,所以.
令,则.
令,,解得;令,,解得,
则 上单调递减,在上单调递增,
因为 ,,
所以 ,
则, ,
故的取值范围为.
【点睛】
本题考查了利用导数研究函数的单调性与零点问题,考查了函数的最值的求法,考查了等价转化方法,考查了推理能力与计算能力,属于难题.
20.(1)当时,在上单调递增;
当时,在上单调递增,在上单调递减;
(2)证明见解析.
【分析】
(1)求出导函数,讨论的取值范围,利用导数与函数单调性之间的关系即可求解.
(2)利用导数求出函数的极大值,由零点存在性定理可得两零点所在的区间,不妨设,则有,构造函数,,利用导数判断出函数单调递增,从而可得,再由即可求解.
【详解】
解:(1)易得函数的定义域为.
对函数求导得:.
当时,恒成立,即可知在上单调递增;
当时,当时,,当时,,
故在上单调递增,在上单调递减.
(2)当时,,,
此时在上单调递增,在上单调递减.
,又,,
不妨设,则有,
令,,
.
当时,,单调递增,
,,
,
又,,
,,在上单调递减,
,即.
【点睛】
本题考查了利用导数研究函数的单调性、利用导数证明不等式,属于难题.
21.(1);(2)证明见解析.
【分析】
(1)对函数求导,分和两种情况,分别判断出函数的单调性与极值,可得的取值范围;
(2)当时,设,成立,即证明,对函数求导判断出单调性和最值,可得命题成立.
【详解】
(1)函数的定义域为,
,
当时,对任意的,,
故在上单调递增,无极值;
当时,当时,,单调递增;
当时,,单调递减.
故在处取得极大值,无极小值.
综上所述,若存在极值,则的取值范围为.
(2)当时,.
设,其定义域为,
则证明即可.
,设,
则,
故函数在上单调递增.
,.
有唯一的实根,且,
.
当时,;
当时,,
故函数的最小值为.
.
.
【点睛】
关键点点睛:本题考查导数解决函数的单调性问题,考查导数证明不等式,解决本题的关键点是构造,将命题成立,转化为证明,对函数求导判断出单调性和最值,可得命题成立,考查学生逻辑推理能力和计算能力,属于中档题.
22.(1)答案见解析;(2)证明见解析.
【分析】
(1)先求出函数的定义域,再求导,当时,导数恒小于零,则可得函数在上为减函数,从而可求出函数的最小值,当时,由导数可得函数在上单调递减,在上单调递增,然后分,和三种情况讨论可求得函数的最小值;
(2)要证,即证,即证,当时,上式恒成立,当时,令,再利用导数可得,从而可得成立.
【详解】
(1)解:函数的定义域是,
.
①当时,,则,
则函数在上单调递减,即函数在区间上单调递减,
故函数在区间上的最小值为.
②当时,令,得;令,得;
故函数在上单调递减,在上单调递增.
(i)当,即时,函数在区间上单调递增,故函数在区间上的最小值为;
(ii)当,即时,函数在区间上单调递减,故函数在区间上的最小值为;
(iii)当,即时,函数在上单调递减,在上单调递增,此时函数在区间上的最小值为.
综上,当时,函数在区间上的最小值为;当时,函数在区间上的最小值为;当时,函数在区间上的最小值为.
(2)证明:当时,,
要证,即证,
因为,所以两边同时乘x,得,
即证.
当时,,而,
所以成立,即成立.
当时,令,
则.
设,,则因为.
因为,所以,
所以当时,单调递增,
所以,即,
所以在上单调递增,
所以,即成立.
综上,对任意,恒有成立.
