3.6二次函数的应用 同步练习(含答案)
文档属性
| 名称 | 3.6二次函数的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
6 二次函数的应用
基础过关
知识点1 用二次函数解决几何图形中的最值问题
1.如图所示,在一个 的内部作一个矩形ABCD,其中AB和BC分别在两直角边上,设AB矩形的面积为 要使矩形的面积最大,x应为( )
B.6 C.15
2.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若 所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)若 求矩形菜园ABCD面积的最大值.
3.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作 垂足为H,连接AF.
(1)求证:
(2)当AE为何值时, 的面积最大
知识点2 用二次函数解决实际问题中的最值问题
4.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售单价定为____________元时,才能使每天所获销售利润最大.
5.某平台食品专营店销售一种饮料,平均每天可售出100箱,每箱利润为20元.为了扩大销售,增加利润,专营店准备适当降价,据测算,若每箱饮料每降价1元,平均每天可多售出50箱,但每箱利润不能低于6元.设每箱饮料降价x元,日均销量为y箱.
(1)求日均销量y关于x的函数关系式;
(2)要使日均利润为3600元,则每箱应降价多少元
(3)如果该专营店想获得最大的日均利润,则每箱饮料应降价多少元 最大日均利润为多少元
6.某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图所示),其中
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大 最大利润是多少
7.为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, 当 时,
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大 最大利润是多少
(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)
知识点3 用二次函数解决抛物线型问题
8.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数 刻画,斜坡可以用一次函数 刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5m时,小球距O点的水平距离为3 m
B.小球距O点的水平距离超过4m呈下降趋势
C.小球落地点距O点的水平距离为7 m
D.斜坡的坡度为1:2
9.某幢建筑物,从10米高的窗口A用水管向外喷水,喷的水流呈抛物线形(抛物线所在平面与墙面垂直),如图,如果抛物线的最高点M离墙1米,离地面40/3米,则水流下落点B离墙的距离OB是( )
A.3米 B.2米 C.5米 D.4米
10.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体A处,另一端固定在离地面高2米的墙体B处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度y(米)与其离墙体A的水平距离x(米)之间的关系满足现测得A,B两墙体之间的水平距离为6米.
(1)直接写出b,c的值;
(2)求大棚的最高处到地面的距离;
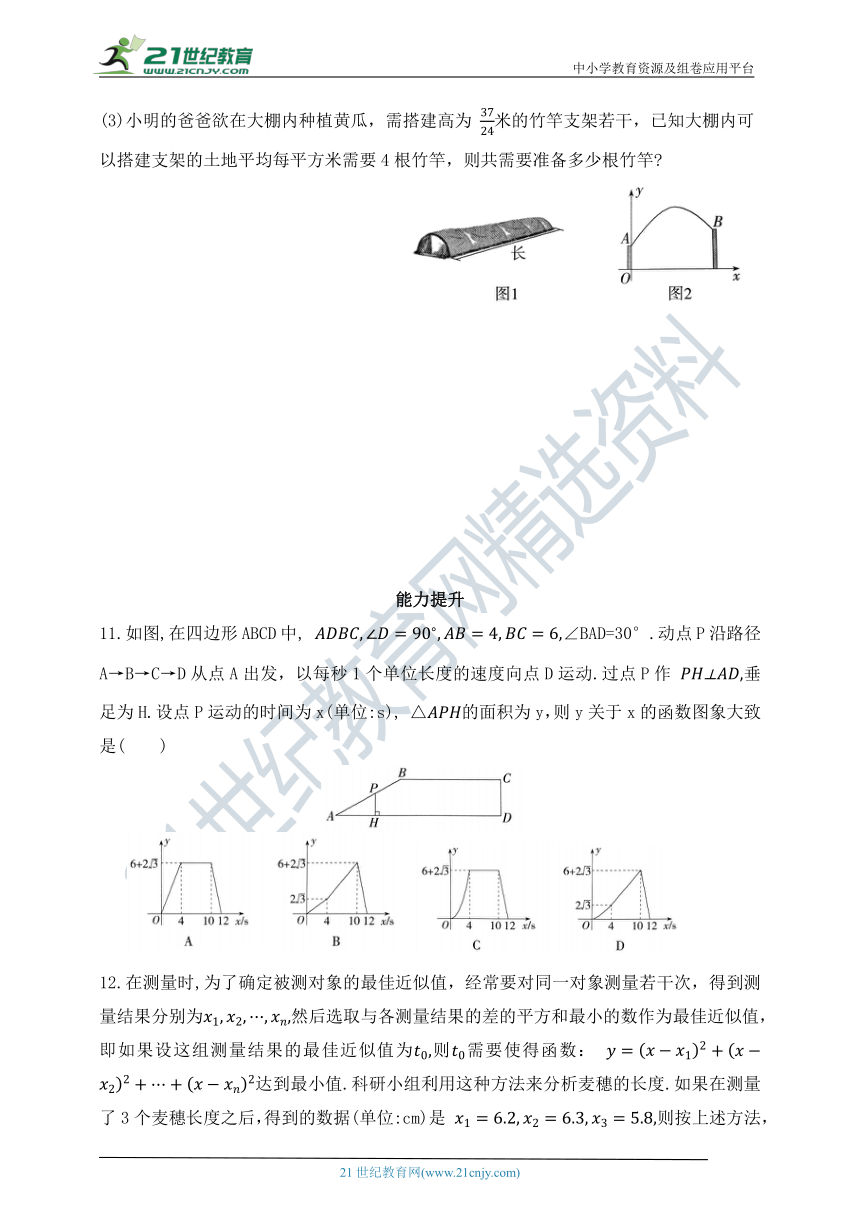
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可
以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿
能力提升
11.如图,在四边形ABCD中, ∠BAD=30°.动点P沿路径A→B→C→D从点A出发,以每秒1个单位长度的速度向点D运动.过点P作 垂足为H.设点P运动的时间为x(单位:s), △的面积为y,则y关于x的函数图象大致是( )
12.在测量时,为了确定被测对象的最佳近似值,经常要对同一对象测量若干次,得到测量结果分别为然后选取与各测量结果的差的平方和最小的数作为最佳近似值,即如果设这组测量结果的最佳近似值为则需要使得函数: 达到最小值.科研小组利用这种方法来分析麦穗的长度.如果在测量了3个麦穗长度之后,得到的数据(单位:cm)是 则按上述方法,可以得到麦穗长的最佳近似长度为___________cm.
13.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
(1)求雕塑高OA;
(2)求落水点C,D之间的距离;
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱 请通过计算说明.
14.某市体育馆为了让来做运动的人方便停车,利用一块矩形空地建了一个停车场,其布局如图所示,已知停车场的长为58米,宽为22米,阴影部分为停车位,其余部分是等宽的通道,已知停车位的面积为700平方米.
(1)求通道的宽是多少米;
(2)该停车场共有车位70个,根据调查分析,当每个车位的月租金为300元时,可全部租出;当每个车位的月租金每上涨10元时,就会少租出1个车位,那么停车场的月租金收入最大为多少元
15.某公司销售一种成本为40元/件的产品,若月销售价格为50元/件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售价格不低于成本.设月销售价格为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当月销售价格是多少元时,月销售利润最大 最大利润是多少万元
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元,已知该公司捐款当月的月销售价格不高于70元/件,月销售最大利润是78万元,求a的值.
16.[数学建模]某地区在2021年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的每千克售价与销售月份之间的关系如图①所示,每千克成本与销售月份之间的关系如图②所示.(其中图①的图象是直线,图②的图象是抛物线,其最低点坐标是(6,1) ).
(1)求每千克蔬菜售价y与销售月份x之间的关系式;
(2)判断哪个月份销售每千克蔬菜的收益(收益=售价-成本)最大 并求最大收益;
(3)求出一年中销售每千克蔬菜的收益大于1元的月份有哪些.
17.[数学建模]如图1,在平面直角坐标系中,O为原点,△OAB是等腰直角三角形, 顶点A(4,0),点B在第一象限,矩形OCDE的顶点 点C
在y轴的正半轴上,点D在第二象限,射线DC经过点B.
(1)求点B的坐标;
(2)将矩形OCDE沿x轴向右平移,得到矩形点O,C,D,E的对应点分别为
设 矩形 与△重叠部分的面积为S.
①如图2,当点. 在x轴正半轴上,且矩形与 重叠部分为四边形时,与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 时,求S的取值范围(直接写出结果即可).
参考答案
基础过关
1.D ∵四边形ABCD是矩形,∴AD∥BC.∴△MAD∽△MBN. 即
∴当 时,矩形的面
积最大.
2.解析 (1)设 米,则 米,
根据题意得 解得
当 时, 不合题意,舍去;
当 时,100-2x=10.
答:AD的长为10米.
(2)设矩形菜园ABCD的面积为S平方米, 米,则 米,
∴当m时,S随m的增大而增大.
∵,∴m=40时,S取得最大值,最大值为
答:若 则矩形菜园ABCD面积的最大值为1200平方米.
3.解析 (1)证明:∵四边形CEFG是正方形, ∵四边形ABCD为矩形,
(2)设 则 当 时,△的面积最大,即当 时,△的面积最大.
4.答案 11
解析 设销售单价定为x(x≥9)元,每天所获利润为y元,则
所以将销售单价定为11元时,才能使每天所获销售利润最大,故填11.
5.解析 (1)日均销量y关于x的函数关系式为
(2)由题意得解得或.
∵,∴舍去.
∴要使日均利润为3600元,则每箱应降价2元.
(3)设销售这种饮料的日均利润为w元,由题意得∴当x=9时,w取得最大值6050.
答:每箱饮料应降价9元,最大日均利润为6050元.
6.解析 (1)设 将(50,100),(80,40)代入,
得 解得
∴
(2)设电商每天获得的利润为w元,则.
∵,∴当x=70时,w取得最大值1800.
答:该电商将每千克的售价定为70元时每天获得的利润最大,最大利润是1800元.
7.解析 (1)设y与x之间的函数关系式为,
依题意,得 解得
∴y与x之间的函数关系式为.
(2)设老张明年种植该作物的总利润为W元,依题意,
得
∵∴当时,W随x的增大而增大.
∵,∴当x=240时,W最大,最大值为
答:当种植面积为240亩时总利润最大,最大利润为268800元.
8.A A项,当 时,整理得 解得
∴当小球抛出高度达到7.5m时,小球距O点的水平距离为3m或5m,
故选项A中结论错误,符合题意;
B项 则抛物线的对称轴为且线
∴当 时,y随x的增大而减小,即小球距O点的水平距离超过4m呈下降趋势,故选项B中结论正确,不符合题意;
C项,联立解得则小球落地点距0点的水平距离为7m,
故选项C中结论正确,不符合题意;
D项,∵斜坡可以用一次函数 刻画,∴斜坡的坡度为1:2,故选项D中结论正确,不符合题意.故选A.
9.A 以O为原点,地面,墙面所在直线为x轴,y轴建立平面直角坐标系,如图.
设抛物线的解析式为
把点A(0,10)代入抛物线解析式得解得
∴抛物线的解析式为
当 时, 解得 (舍去),=3.∴OB=3米.故选A.
10.解析
(2)由
可得当 时,y有最大值,即大棚最高处到地面的距离为米。
(3)由 解得 又因为0≤x≤6,
所以大棚内可以搭建支架的土地的宽为 (米),
又大棚的长为16米,所以需要搭建支架部分的土地面积为 (平方米),
故共需要 (根)竹竿.
能力提升
11.D ①当点P在AB上运动时,
为二次函数.
②当点P在BC上运动时,如图.
由①知
则 为一次函数.
③当点P在CD上运动时,同理可得 为一次函数.故选D.
12.答案 6.1
解析
当 时,y取得最小值,故最佳近似长度为6.1 cm.
13.解析 (1)当x=0时, ∴雕塑高
(2)当y=0时, 解得(舍去),.
(3)当时
顶部F不会碰到水柱.
14.解析 (1)设通道的宽为x米,根据题意,得
解得x=36(舍去)或x=4.
答:通道的宽为4米.
(2)设月租金上涨a元,停车场的月租金收入为w元,
根据题意,得 当 时,w取得最大值,最大值为25000.
∴停车场的月租金收入最大为25000元.
15.解析 (1)由题意,得
(2)设月销售利润为z万元,由题意,得
∴当 时,z有最大值90.
即当月销售价格是70元/件时,月销售利润最大,最大利润是90万元.
(3)由题意,得
此函数图象的对称轴为
∴当月销售价格是70元/件时,月销售利润最大,为78万元.
解得.∴a的值为4.
16.解析 (1)设每千克蔬菜售价y与销售月份x之间的关系式为
将(3,5)和(6,3)代入,得 解得
∴每千克蔬菜售价y与销售月份x之间的关系式为
(2)设每千克成本与销售月份之间的关系式为把(3,4)代入,得 解得 即
设销售每千克蔬菜的收益为w元,则 ∴当x=5时,w有最大值,最大值为
∴5月份销售每千克蔬菜的收益最大,最大收益为 元.
当w=1时, 解得
x为正整数,∴一年中销售每千克蔬菜的收益大于1元的月份有4,5,6三个月.
17.解析 (1)如图,过点B作 垂足为H.由点A(4,0),得OA=4.
∵BO=BA,∠OBA=90°,
∴点B的坐标为(2,2).
(2)①由点 得
由平移知,
∵BO=BA,∠OBA=90°,∴∠BOA=∠BAO=45°.
即 其中t的取值范围是
解法提示:a.当 时,如图1,
当 时,S取最小值,最小值为
当 时,S取最大值,最大值为
b.当 时,如图2,
当 时,S取最大值,最大值为
当 或4时,
∴
c.当 时,如图3,
当t=4时,S取最大值,最大值为
当 时,S取最小值,最小值为
综上可知,当 时,S的取值范围为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
6 二次函数的应用
基础过关
知识点1 用二次函数解决几何图形中的最值问题
1.如图所示,在一个 的内部作一个矩形ABCD,其中AB和BC分别在两直角边上,设AB矩形的面积为 要使矩形的面积最大,x应为( )
B.6 C.15
2.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若 所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)若 求矩形菜园ABCD面积的最大值.
3.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作 垂足为H,连接AF.
(1)求证:
(2)当AE为何值时, 的面积最大
知识点2 用二次函数解决实际问题中的最值问题
4.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售单价定为____________元时,才能使每天所获销售利润最大.
5.某平台食品专营店销售一种饮料,平均每天可售出100箱,每箱利润为20元.为了扩大销售,增加利润,专营店准备适当降价,据测算,若每箱饮料每降价1元,平均每天可多售出50箱,但每箱利润不能低于6元.设每箱饮料降价x元,日均销量为y箱.
(1)求日均销量y关于x的函数关系式;
(2)要使日均利润为3600元,则每箱应降价多少元
(3)如果该专营店想获得最大的日均利润,则每箱饮料应降价多少元 最大日均利润为多少元
6.某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图所示),其中
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大 最大利润是多少
7.为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, 当 时,
(1)求y与x之间的函数关系式(不求自变量的取值范围);
(2)受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大 最大利润是多少
(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)
知识点3 用二次函数解决抛物线型问题
8.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数 刻画,斜坡可以用一次函数 刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5m时,小球距O点的水平距离为3 m
B.小球距O点的水平距离超过4m呈下降趋势
C.小球落地点距O点的水平距离为7 m
D.斜坡的坡度为1:2
9.某幢建筑物,从10米高的窗口A用水管向外喷水,喷的水流呈抛物线形(抛物线所在平面与墙面垂直),如图,如果抛物线的最高点M离墙1米,离地面40/3米,则水流下落点B离墙的距离OB是( )
A.3米 B.2米 C.5米 D.4米
10.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体A处,另一端固定在离地面高2米的墙体B处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度y(米)与其离墙体A的水平距离x(米)之间的关系满足现测得A,B两墙体之间的水平距离为6米.
(1)直接写出b,c的值;
(2)求大棚的最高处到地面的距离;
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可
以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿
能力提升
11.如图,在四边形ABCD中, ∠BAD=30°.动点P沿路径A→B→C→D从点A出发,以每秒1个单位长度的速度向点D运动.过点P作 垂足为H.设点P运动的时间为x(单位:s), △的面积为y,则y关于x的函数图象大致是( )
12.在测量时,为了确定被测对象的最佳近似值,经常要对同一对象测量若干次,得到测量结果分别为然后选取与各测量结果的差的平方和最小的数作为最佳近似值,即如果设这组测量结果的最佳近似值为则需要使得函数: 达到最小值.科研小组利用这种方法来分析麦穗的长度.如果在测量了3个麦穗长度之后,得到的数据(单位:cm)是 则按上述方法,可以得到麦穗长的最佳近似长度为___________cm.
13.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
(1)求雕塑高OA;
(2)求落水点C,D之间的距离;
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱 请通过计算说明.
14.某市体育馆为了让来做运动的人方便停车,利用一块矩形空地建了一个停车场,其布局如图所示,已知停车场的长为58米,宽为22米,阴影部分为停车位,其余部分是等宽的通道,已知停车位的面积为700平方米.
(1)求通道的宽是多少米;
(2)该停车场共有车位70个,根据调查分析,当每个车位的月租金为300元时,可全部租出;当每个车位的月租金每上涨10元时,就会少租出1个车位,那么停车场的月租金收入最大为多少元
15.某公司销售一种成本为40元/件的产品,若月销售价格为50元/件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售价格不低于成本.设月销售价格为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当月销售价格是多少元时,月销售利润最大 最大利润是多少万元
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元,已知该公司捐款当月的月销售价格不高于70元/件,月销售最大利润是78万元,求a的值.
16.[数学建模]某地区在2021年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的每千克售价与销售月份之间的关系如图①所示,每千克成本与销售月份之间的关系如图②所示.(其中图①的图象是直线,图②的图象是抛物线,其最低点坐标是(6,1) ).
(1)求每千克蔬菜售价y与销售月份x之间的关系式;
(2)判断哪个月份销售每千克蔬菜的收益(收益=售价-成本)最大 并求最大收益;
(3)求出一年中销售每千克蔬菜的收益大于1元的月份有哪些.
17.[数学建模]如图1,在平面直角坐标系中,O为原点,△OAB是等腰直角三角形, 顶点A(4,0),点B在第一象限,矩形OCDE的顶点 点C
在y轴的正半轴上,点D在第二象限,射线DC经过点B.
(1)求点B的坐标;
(2)将矩形OCDE沿x轴向右平移,得到矩形点O,C,D,E的对应点分别为
设 矩形 与△重叠部分的面积为S.
①如图2,当点. 在x轴正半轴上,且矩形与 重叠部分为四边形时,与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 时,求S的取值范围(直接写出结果即可).
参考答案
基础过关
1.D ∵四边形ABCD是矩形,∴AD∥BC.∴△MAD∽△MBN. 即
∴当 时,矩形的面
积最大.
2.解析 (1)设 米,则 米,
根据题意得 解得
当 时, 不合题意,舍去;
当 时,100-2x=10.
答:AD的长为10米.
(2)设矩形菜园ABCD的面积为S平方米, 米,则 米,
∴当m时,S随m的增大而增大.
∵,∴m=40时,S取得最大值,最大值为
答:若 则矩形菜园ABCD面积的最大值为1200平方米.
3.解析 (1)证明:∵四边形CEFG是正方形, ∵四边形ABCD为矩形,
(2)设 则 当 时,△的面积最大,即当 时,△的面积最大.
4.答案 11
解析 设销售单价定为x(x≥9)元,每天所获利润为y元,则
所以将销售单价定为11元时,才能使每天所获销售利润最大,故填11.
5.解析 (1)日均销量y关于x的函数关系式为
(2)由题意得解得或.
∵,∴舍去.
∴要使日均利润为3600元,则每箱应降价2元.
(3)设销售这种饮料的日均利润为w元,由题意得∴当x=9时,w取得最大值6050.
答:每箱饮料应降价9元,最大日均利润为6050元.
6.解析 (1)设 将(50,100),(80,40)代入,
得 解得
∴
(2)设电商每天获得的利润为w元,则.
∵,∴当x=70时,w取得最大值1800.
答:该电商将每千克的售价定为70元时每天获得的利润最大,最大利润是1800元.
7.解析 (1)设y与x之间的函数关系式为,
依题意,得 解得
∴y与x之间的函数关系式为.
(2)设老张明年种植该作物的总利润为W元,依题意,
得
∵∴当时,W随x的增大而增大.
∵,∴当x=240时,W最大,最大值为
答:当种植面积为240亩时总利润最大,最大利润为268800元.
8.A A项,当 时,整理得 解得
∴当小球抛出高度达到7.5m时,小球距O点的水平距离为3m或5m,
故选项A中结论错误,符合题意;
B项 则抛物线的对称轴为且线
∴当 时,y随x的增大而减小,即小球距O点的水平距离超过4m呈下降趋势,故选项B中结论正确,不符合题意;
C项,联立解得则小球落地点距0点的水平距离为7m,
故选项C中结论正确,不符合题意;
D项,∵斜坡可以用一次函数 刻画,∴斜坡的坡度为1:2,故选项D中结论正确,不符合题意.故选A.
9.A 以O为原点,地面,墙面所在直线为x轴,y轴建立平面直角坐标系,如图.
设抛物线的解析式为
把点A(0,10)代入抛物线解析式得解得
∴抛物线的解析式为
当 时, 解得 (舍去),=3.∴OB=3米.故选A.
10.解析
(2)由
可得当 时,y有最大值,即大棚最高处到地面的距离为米。
(3)由 解得 又因为0≤x≤6,
所以大棚内可以搭建支架的土地的宽为 (米),
又大棚的长为16米,所以需要搭建支架部分的土地面积为 (平方米),
故共需要 (根)竹竿.
能力提升
11.D ①当点P在AB上运动时,
为二次函数.
②当点P在BC上运动时,如图.
由①知
则 为一次函数.
③当点P在CD上运动时,同理可得 为一次函数.故选D.
12.答案 6.1
解析
当 时,y取得最小值,故最佳近似长度为6.1 cm.
13.解析 (1)当x=0时, ∴雕塑高
(2)当y=0时, 解得(舍去),.
(3)当时
顶部F不会碰到水柱.
14.解析 (1)设通道的宽为x米,根据题意,得
解得x=36(舍去)或x=4.
答:通道的宽为4米.
(2)设月租金上涨a元,停车场的月租金收入为w元,
根据题意,得 当 时,w取得最大值,最大值为25000.
∴停车场的月租金收入最大为25000元.
15.解析 (1)由题意,得
(2)设月销售利润为z万元,由题意,得
∴当 时,z有最大值90.
即当月销售价格是70元/件时,月销售利润最大,最大利润是90万元.
(3)由题意,得
此函数图象的对称轴为
∴当月销售价格是70元/件时,月销售利润最大,为78万元.
解得.∴a的值为4.
16.解析 (1)设每千克蔬菜售价y与销售月份x之间的关系式为
将(3,5)和(6,3)代入,得 解得
∴每千克蔬菜售价y与销售月份x之间的关系式为
(2)设每千克成本与销售月份之间的关系式为把(3,4)代入,得 解得 即
设销售每千克蔬菜的收益为w元,则 ∴当x=5时,w有最大值,最大值为
∴5月份销售每千克蔬菜的收益最大,最大收益为 元.
当w=1时, 解得
x为正整数,∴一年中销售每千克蔬菜的收益大于1元的月份有4,5,6三个月.
17.解析 (1)如图,过点B作 垂足为H.由点A(4,0),得OA=4.
∵BO=BA,∠OBA=90°,
∴点B的坐标为(2,2).
(2)①由点 得
由平移知,
∵BO=BA,∠OBA=90°,∴∠BOA=∠BAO=45°.
即 其中t的取值范围是
解法提示:a.当 时,如图1,
当 时,S取最小值,最小值为
当 时,S取最大值,最大值为
b.当 时,如图2,
当 时,S取最大值,最大值为
当 或4时,
∴
c.当 时,如图3,
当t=4时,S取最大值,最大值为
当 时,S取最小值,最小值为
综上可知,当 时,S的取值范围为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
