青岛版九年级上册1.4图形的位似课件(共16张PPT)
文档属性
| 名称 | 青岛版九年级上册1.4图形的位似课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 189.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-03 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
§1.4图形的位似(2)
青岛版 数学 九(上) 第一章 图形的相似
平面直角坐标系中的位似图形
1、什么叫做位似图形
3、判断两个多边形是位似图形的方法步骤:
2、位似图形与相似图形有什么关系?
5、位似图形的性质:
4、两个位似图形相对于位似中心有几种位置关系?
知识回顾
●
B'
A'
●
x
y
B
A
o
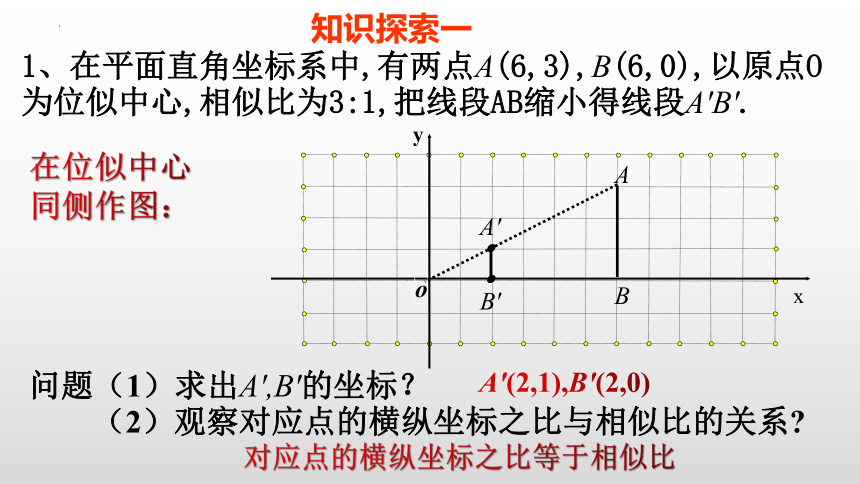
1、在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小得线段A′B′.
A′(2,1),B′(2,0)
问题(1)求出A′,B′的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
知识探索一
在位似中心
同侧作图:
对应点的横纵坐标之比等于相似比
●
A'
B'
●
x
y
B
A
o
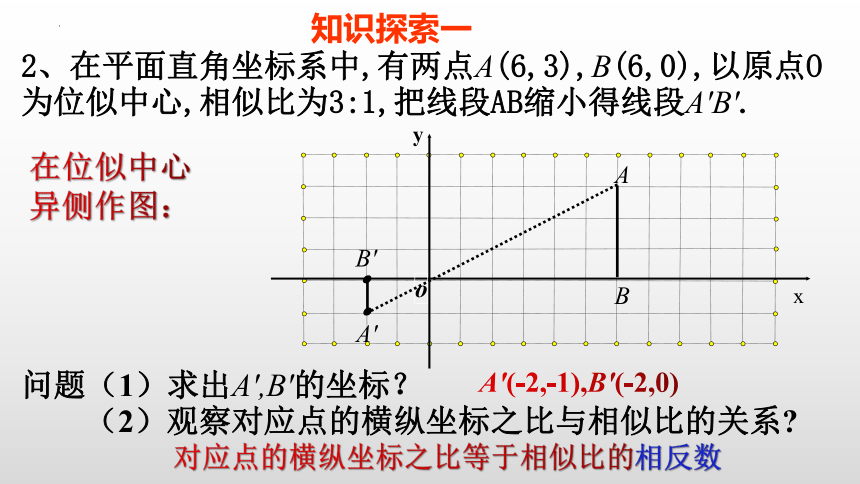
2、在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小得线段A′B′.
A′(-2,-1),B′(-2,0)
问题(1)求出A′,B′的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
知识探索一
在位似中心
异侧作图:
对应点的横纵坐标之比等于相似比的相反数
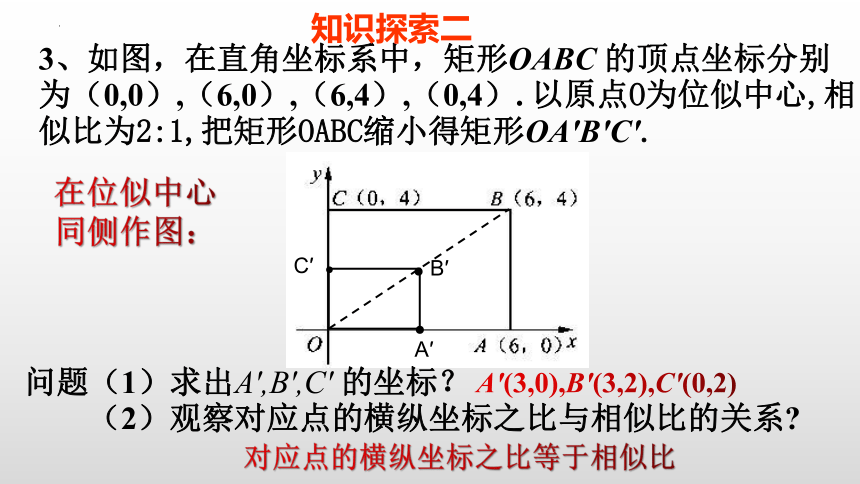
3、如图,在直角坐标系中,矩形OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 以原点O为位似中心,相似比为2:1,把矩形OABC缩小得矩形OA′B′C′.
●
A′
● B′
C′ ●
知识探索二
在位似中心
同侧作图:
问题(1)求出A′,B′,C′ 的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
对应点的横纵坐标之比等于相似比
A′(3,0),B′(3,2),C′(0,2)
4、如图,在直角坐标系中,矩形OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 以原点O为位似中心,相似比为2:1,把矩形OABC缩小得矩形OA′B′C′.
A′
●
B′●
● C′
知识探索二
在位似中心
异侧作图:
问题(1)求出A′,B′,C′ 的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
A′(-3,0),B′(-3,-2),C′(0,-2)
对应点的横纵坐标之比等于相似比的相反数
在平面直角坐标系中,若两图形关于原点位似,那么对应点的横、纵坐标之比等于相似比(同侧)或相似比的相反数(异侧).
1、平面直角坐标系中的位似规律:
课内知识总结
例题精讲
例1、如图,△AOB缩小后得到△COD,△AOB与△COD的
相似比为3,若点C(1,2),则点A的坐标是( )
A.(2,4) B.(2,6) C.(3,6) D.(3,4)
例2、如图,正方形OABC与正方形ODEF是位似图形,点O是位似中心,且相似比为 ,点A(1,0),则点E坐标是( )
A.( , ) B.( ,0) C.(0, ) D.(2,2)
x
y
O
A
B
C
D
x
y
O
A
B
C
D
E
F
C
A
例题精讲
x
y
O
A
B
B′
A′
例3、如图,在平面直角坐标系中,若△AOB与△A′OB′是关于点O为位似中心的位似图形,,且相似比为3:2,已知点A(2,2),B(3,﹣2), 则B′的坐标是( )
A.(﹣2,4) B.(﹣2, ) C.(﹣2, 2) D.(-2, )
B
例题精讲
例4、在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为1:2 ,把△EFO缩小,
则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)或(8,﹣4)
C.(﹣8,4) D.(﹣2,1)或(2,﹣1)
D
例题精讲
例5、如图,在平面直角坐标系中,若△ABC与△DEF是
位似图形,,且点E(5,0),B(3,0), 则其位似中心的坐标
是( )
A.(0,0) B.(1, 1 ) C.(0,1) D.(1, 0 )
B
E
A
C
x
y
D
F
D
例题精讲
例6、在平面直角坐标系中,已知点C(2,3),D(1,0),现以原点O为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标____________。
(4,6)或(-4,-6)
能力拔高
B
A
C
D
E
O
x
y
例7、已知:在平面直角坐标系中,△ABC与△ADE关于点A位似,位似比为2:1,且点A(-1,0),点B的横坐标为a.则点D的横坐标为_________。
B
A
C
D
E
O
x
y
在平面直角坐标系中,若两图形关于原点位似,那么对应点的横、纵坐标之比等于相似比(同侧)或相似比的相反数(异侧).
1、平面直角坐标系中的位似规律:
知识总结
注意: 在平面直角坐标系中,若两图形不是关于原点位似时,先通过平移,再利用规律解题.
作业布置
课本P30 练习题 第1、2题
同学们,再见
§1.4图形的位似(2)
青岛版 数学 九(上) 第一章 图形的相似
平面直角坐标系中的位似图形
1、什么叫做位似图形
3、判断两个多边形是位似图形的方法步骤:
2、位似图形与相似图形有什么关系?
5、位似图形的性质:
4、两个位似图形相对于位似中心有几种位置关系?
知识回顾
●
B'
A'
●
x
y
B
A
o
1、在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小得线段A′B′.
A′(2,1),B′(2,0)
问题(1)求出A′,B′的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
知识探索一
在位似中心
同侧作图:
对应点的横纵坐标之比等于相似比
●
A'
B'
●
x
y
B
A
o
2、在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小得线段A′B′.
A′(-2,-1),B′(-2,0)
问题(1)求出A′,B′的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
知识探索一
在位似中心
异侧作图:
对应点的横纵坐标之比等于相似比的相反数
3、如图,在直角坐标系中,矩形OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 以原点O为位似中心,相似比为2:1,把矩形OABC缩小得矩形OA′B′C′.
●
A′
● B′
C′ ●
知识探索二
在位似中心
同侧作图:
问题(1)求出A′,B′,C′ 的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
对应点的横纵坐标之比等于相似比
A′(3,0),B′(3,2),C′(0,2)
4、如图,在直角坐标系中,矩形OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4). 以原点O为位似中心,相似比为2:1,把矩形OABC缩小得矩形OA′B′C′.
A′
●
B′●
● C′
知识探索二
在位似中心
异侧作图:
问题(1)求出A′,B′,C′ 的坐标?
(2)观察对应点的横纵坐标之比与相似比的关系
A′(-3,0),B′(-3,-2),C′(0,-2)
对应点的横纵坐标之比等于相似比的相反数
在平面直角坐标系中,若两图形关于原点位似,那么对应点的横、纵坐标之比等于相似比(同侧)或相似比的相反数(异侧).
1、平面直角坐标系中的位似规律:
课内知识总结
例题精讲
例1、如图,△AOB缩小后得到△COD,△AOB与△COD的
相似比为3,若点C(1,2),则点A的坐标是( )
A.(2,4) B.(2,6) C.(3,6) D.(3,4)
例2、如图,正方形OABC与正方形ODEF是位似图形,点O是位似中心,且相似比为 ,点A(1,0),则点E坐标是( )
A.( , ) B.( ,0) C.(0, ) D.(2,2)
x
y
O
A
B
C
D
x
y
O
A
B
C
D
E
F
C
A
例题精讲
x
y
O
A
B
B′
A′
例3、如图,在平面直角坐标系中,若△AOB与△A′OB′是关于点O为位似中心的位似图形,,且相似比为3:2,已知点A(2,2),B(3,﹣2), 则B′的坐标是( )
A.(﹣2,4) B.(﹣2, ) C.(﹣2, 2) D.(-2, )
B
例题精讲
例4、在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为1:2 ,把△EFO缩小,
则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)或(8,﹣4)
C.(﹣8,4) D.(﹣2,1)或(2,﹣1)
D
例题精讲
例5、如图,在平面直角坐标系中,若△ABC与△DEF是
位似图形,,且点E(5,0),B(3,0), 则其位似中心的坐标
是( )
A.(0,0) B.(1, 1 ) C.(0,1) D.(1, 0 )
B
E
A
C
x
y
D
F
D
例题精讲
例6、在平面直角坐标系中,已知点C(2,3),D(1,0),现以原点O为位似中心,将线段CD放大得到线段AB,若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标____________。
(4,6)或(-4,-6)
能力拔高
B
A
C
D
E
O
x
y
例7、已知:在平面直角坐标系中,△ABC与△ADE关于点A位似,位似比为2:1,且点A(-1,0),点B的横坐标为a.则点D的横坐标为_________。
B
A
C
D
E
O
x
y
在平面直角坐标系中,若两图形关于原点位似,那么对应点的横、纵坐标之比等于相似比(同侧)或相似比的相反数(异侧).
1、平面直角坐标系中的位似规律:
知识总结
注意: 在平面直角坐标系中,若两图形不是关于原点位似时,先通过平移,再利用规律解题.
作业布置
课本P30 练习题 第1、2题
同学们,再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
